博客作业06--图

1.学习总结

1.1图的思维导图

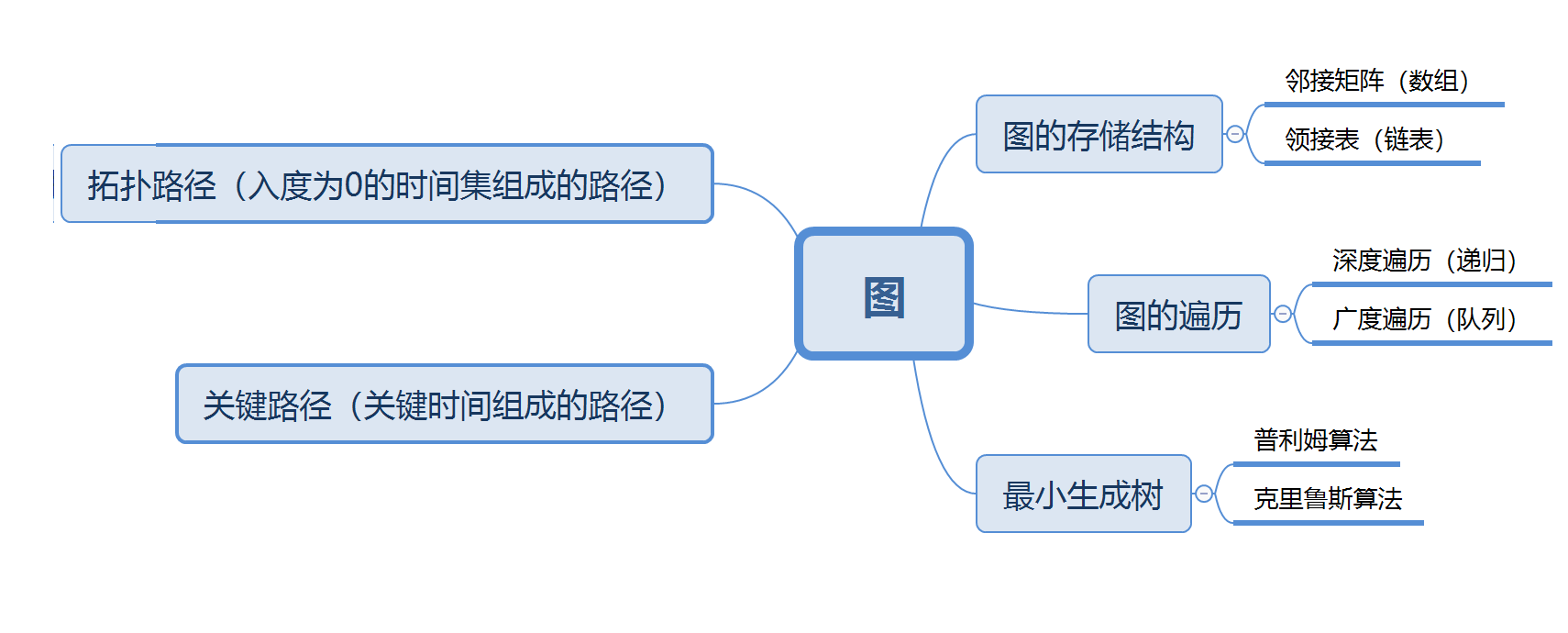
1.2 图结构学习体会

• 深度遍历算法、广度遍历算法都是遍历图的算法。深度优先遍历的策略就是首先访问第一个邻接结点，然后再以这个被访问的邻接结点作为初始结点，访问它的第一个邻接结点；广度遍历类似于一个分层搜索的过程，广度优先遍历需要使用一个队列以保持访问过的结点的顺序，以便按这个顺序来访问这些结点的邻接结点。Prim和Kruscal算法都是生成最小生成树的算法。从策略上来说，Prim算法是直接查找，多次寻找邻边的权重最小值，而Kruskal是需要先对权重排序后查找的；Kruskal在算法效率上是比Prim快的，因为Kruskal只需一次对权重的排序就能找到最小生成树，而Prim算法需要多次对邻边排序才能找到。Dijkstra算法是解决最短路径问题，Dijkstra算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，算法最终得到一个最短路径树；Dijkstra算法采用的是一种贪心的策略，声明一个数组dis来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合。拓扑排序算法，是将一个有向无环图G的所有的顶点排成一个线性序列，使得有向图中的任意的顶点u 和 v 构成的弧<u， v>属于该图的边集，并且使得 u 始终是出现在 v 的前面。

2.PTA实验作业

题目1：7-1 图着色问题

1.设计思路

main函数
输入v，e，k
建图CreateAdj( G,v,e )
输入n
while(n--)
    set <int> E
    flag=true
    for i=1 to i<=v
    输入color[i]，并且E.insert(color[i])，visit[i] = 0。
end
定义一个l=E.size()
若输入的颜色种类不等于k
    cout<<No，continue。
do{
    for(  i=1, i<=v&&flag ; i++ )
      若visit[i]==0 {
	则调用Check( G,k,i );
	break;}
}while( flag && i<=v );
若 flag ==1，则cout << "Yes" 
否则	cout << "No" 
Check函数
建立一个指针指向顶点v，令visit[v]=1，表示已经遍历过了。
while(p)
    若color[p->adjvex]==color[v]，则说明顶点相邻的点颜色相同
    flag=false。
   若!visit[p->adjvex],则递归搜索。
     p=p->nextarc
end

2.代码截图

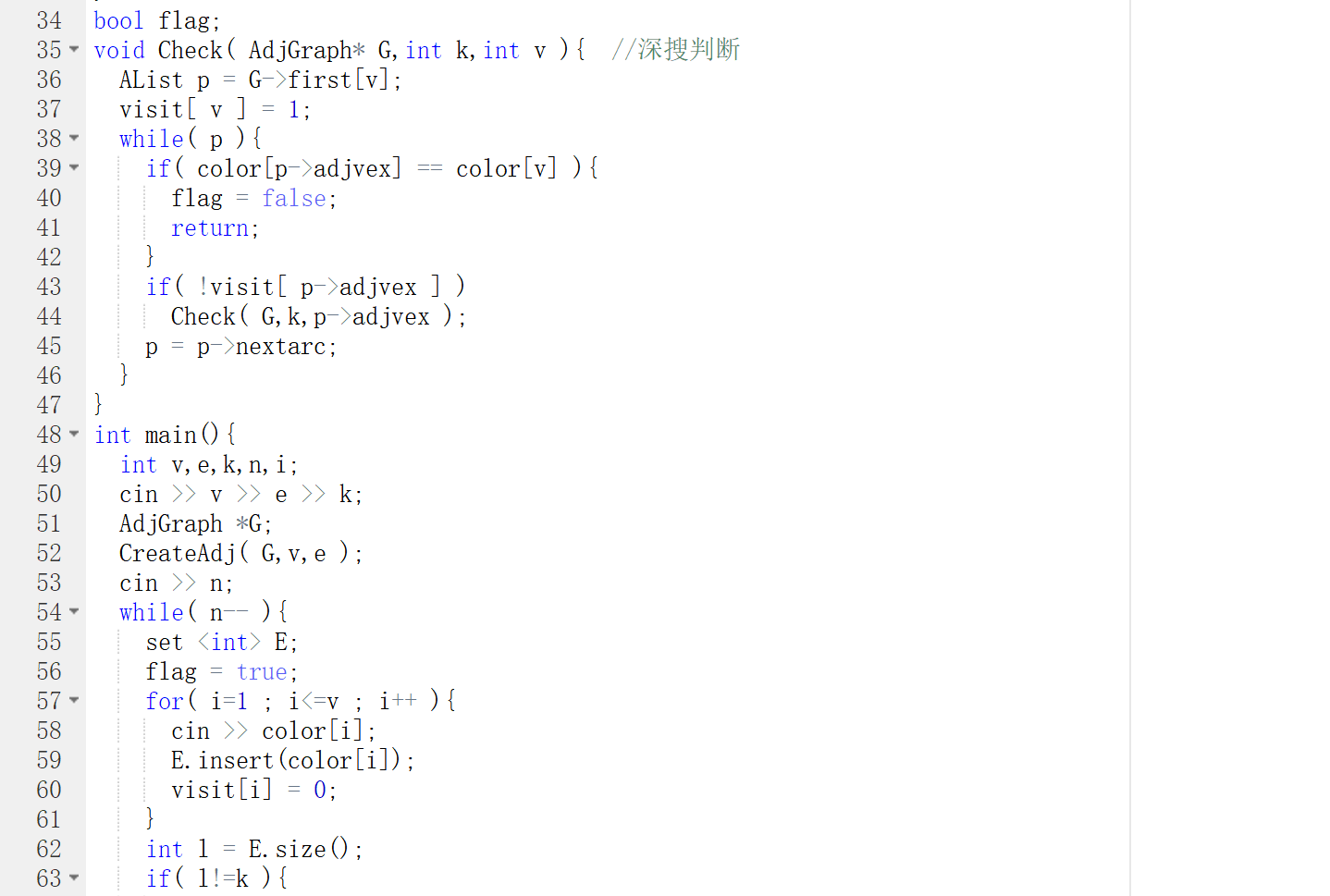
3.PTA提交列表说明

• 刚开始只用了一次循环来判断着色，可能会漏掉一些顶点，导致图不连通。后来，在外面又嵌套了一层循环就解决了。

题目2：7-3 六度空间

1.设计思路

建立一个队列queue <int> q，用来解决层数问题。
遍历过的x，令visit[x]=1，并将x入队q
定义lengh=1来表示层数，last=x保存每一层最后一个顶点，count=1计数人数。
while(!q.empty())
    定义v=q.front()，定义一个指针p指向v
    遍历该层所有顶点，若该点未遍历则count++,若lengh<6层，则将该点入队。
    若last==v，则lengh++，并且last=q.back()
end
输出x,100.0*count/G->n。

2.代码截图

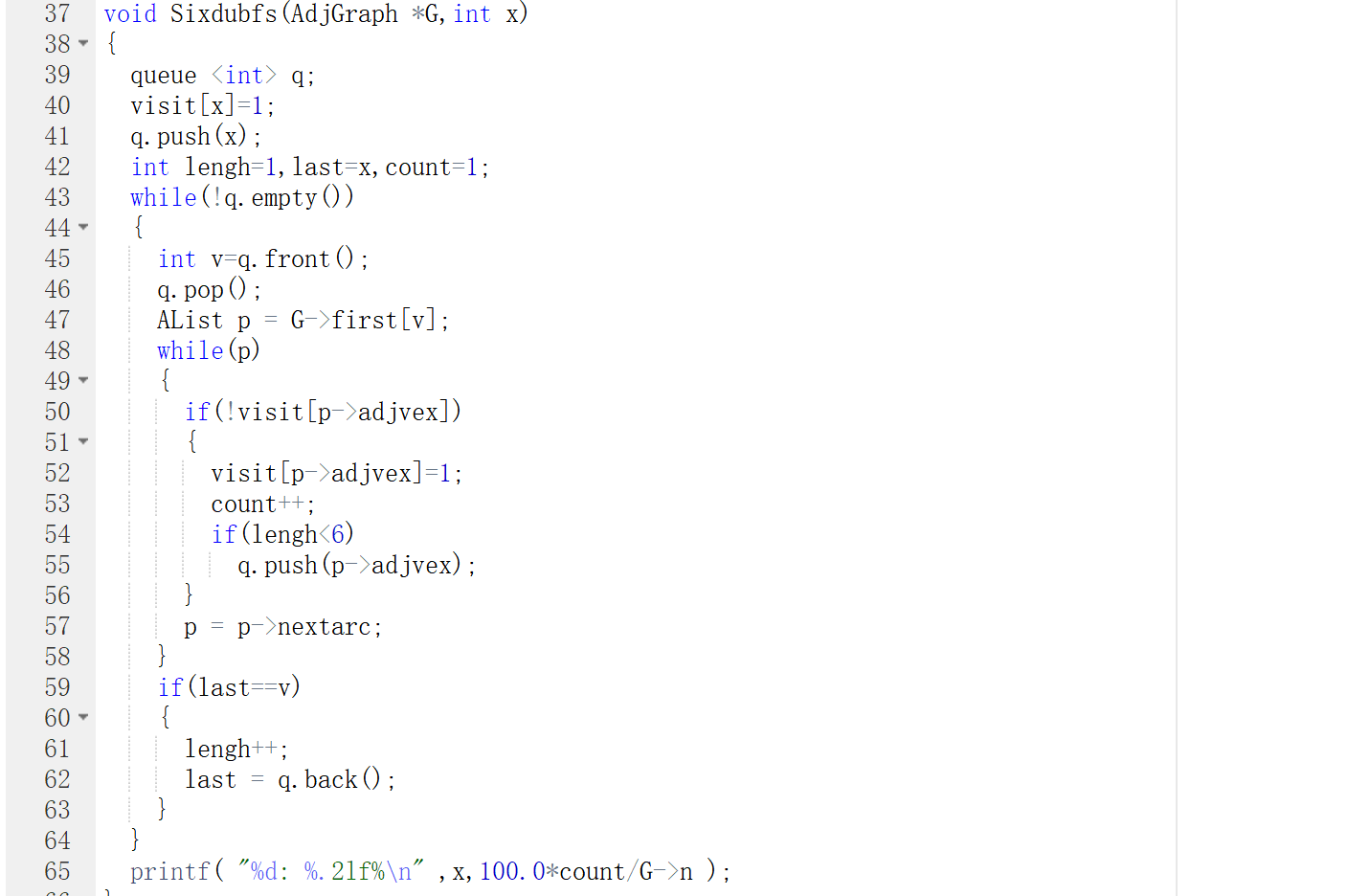
3.PTA提交列表说明

• 本题一开始不大理解六度是什么意思，后来再查找相关题目理解意思后就明白了。

题目3：7-5 畅通工程之最低成本建设问题

1.设计思路

这题的基本思路就是利用prim算法构建最小生成树。

2.代码截图

3.PTA提交列表说明

• 没有问题

3.截图本周题目集的PTA最后排名

3.1 PTA排名

3.2 我的得分：2.5

4. 阅读代码

匈牙利算法

#include<cstdio>  
#include<cstring>  
using namespace std;  
  
int n,m,ans;  
int match[210];//母牛i的配偶是公牛match[i]  
bool chw[210];//在此趟询问中，母牛i是否被询问过  
bool mp[210][210];//公牛i与母牛j是否有关系  
  
bool find_ans(int x)  
{  
    for(int i=1;i<=m;i++)  
    {  
        if(mp[x][i]==true&&chw[i]==true)  
        {  
            chw[i]=false;  
            if(match[i]==0||find_ans(match[i])==true)  
            //母牛没有配偶||匹配该母牛的公牛能否换一头母牛匹配   
            {  
                match[i]=x;  
                return true;  
            }  
        }  
    }  
    return false;  
}  
  
int main()  
{  
    while(scanf("%d %d",&n,&m)!=EOF)  
    {  
        memset(mp,false,sizeof(mp));  
        for(int i=1;i<=n;i++)  
        {  
            int k,x;  
            scanf("%d",&k);  
            for(int j=1;j<=k;j++)  
            {  
                scanf("%d",&x);  
                mp[i][x]=true;  
            }  
        }  
        ans=0;  
        memset(match,0,sizeof(match));  
        for(int i=1;i<=n;i++)  
        {  
            memset(chw,true,sizeof(chw));  
            if(find_ans(i)==true) ans++;  
        }  
        printf("%d\n",ans);  
    }  
    return 0;  
}  

• 公牛是二分图的一个集合，母牛也是。接着公牛逐一询问母牛，会出现两种情况。1、如果母牛未被匹配，公牛匹配它；2、如果母牛已被匹配，询问母牛的原配公牛能否换另一头母牛匹配。若行，则该公牛可以获得此母牛；反之，该公牛无法得到该母牛。如果该失配公牛问遍了所有母牛，仍然不能找到合适的配偶，则该公牛匹配失败（ans不能+1）。匈牙利算法是众多用于解决线性任务分配问题的算法之一，是用来解决二分图最大匹配问题的经典算法，可以在多项式时间内解决问题。

5. 代码Git提交记录截图