Upd:回去仔细看了下知乎，发现有人挂了一篇文章（链接），更具参考性。##
前言（流水账）：事情的起因很简单，生物课上讲到碱基互补配对原则，讲到不限制碱基对数目的情况下，\(n\) 对碱基对组成的 DNA 序列理论上有 \(4^n\) 种。咋一看，\(4^n\) 从一端开始枚举一条单链，乘法原理来解释似乎没有什么问题，但是我细心的同学（BeyondLimits 关键人物）发现事情不太对劲，认为数量应该要再除以 \(2\)，即 \(\frac{4^n}{2}\)，但是我觉得好像还是不太对，经过讨论，我们觉得这个猜想也不太对...后来发现知乎上也有这个问题的讨论（链接），却没有给出明确结论。
开始我们认为一个 DNA 序列会被计算 \(2\) 次。但是了手推 \(2\) 个碱基对的 DNA 序列数量，发现和 \(\frac{4^n}{2}\) 的猜想不符合。我们又考虑到字符串有特殊性质，就开始考虑一些具有特殊性质的字符串，并且写了一些错误的程序来模拟枚举的过程...程序毕竟是错的，折腾很久都没什么进展。
从中午一路犯错到晚上，凌晨我们又和另一位同学（thorn 关键人物）一起讨论。又一番瞎折腾，才搞出了这个问题的结果。
打表发现：
\(n=2\) 时 DNA 序列有 \(10\) 种
\(n=3\) 时 DNA 序列有 \(32\) 种
\(n=4\) 时 DNA 序列有 \(136\) 种
\(n=5\) 时 DNA 序列有 \(512\) 种
\(n=6\) 时 DNA 序列有 \(2080\) 种
\(...\)
发现只有 \(n\) 为奇数满足这个猜想，偶数则不行。
回到最初的观点上，我们认为一个 DNA 序列会被计算 \(2\) 次。因为：
但是结果于猜想不符，我们猜测可能有其他的串被计算到的次数不是 \(2\) 次。
存在被统计次数大于 \(2\) 的串吗？不存在，每条 DNA 从两条链的 3‘ 端开始只有两种结果。
但是这两种结果可能会相同？
如果我们按照 \(4^n\) 来从 3’ 端逐个地枚举一条 DNA 单链上的碱基排列顺序的话，会有这样的一种“对称”的串 \(S\) 从两个 3‘ 端开始结果一样，只会被枚举到 \(1\) 次。
如图所示是一个串 \(S\) 的例子：
且因为这个特殊性质，串 \(S\) 的长度只能为偶数，因为若长度为奇数，则最中间的碱基从两个 3‘ 端开始枚举必然是不相同的。
还有一个问题就是怎么计算 DNA 序列的数目。
在枚举到的 \(4^n\) 种情况中，有些事被枚举到两次的串，有些则是只被枚举到一次的串。
只要计算出只被枚举到一次的串的数量就可以算出偶数个碱基对组成的 DNA 序列理论上的种类了。
可以确定 DNA 一条单链的前一半，再用前一半去确定后一半，如图：
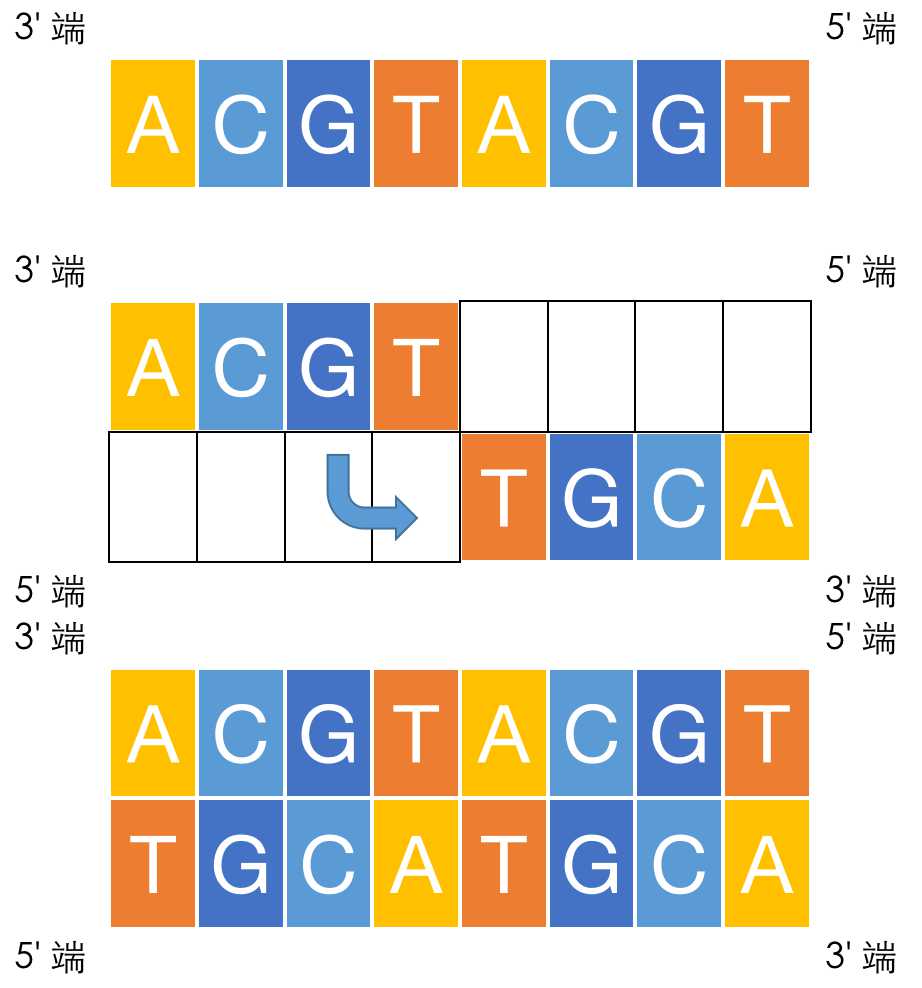
对于 \(n\)（偶数）个碱基对 DNA 序列中，有 \(4^{\frac{n}{2}}\) 种串（序列）只会被统计到一次。
\(n\)（奇数）个则每个串（序列）都被统计两次。
所以结论是这样
\(a_n=\begin{cases}\frac{4^n}{2}\ \ \ \ \ \ \ \ n=2k+1\\\frac{4^n+4^{\frac{n}{2}}}{2}\ n=2k\ \ (k\in N^*)\end{cases}\)
但是事实上 DNA 更复杂，这个结论也只能是理论上的了。
最后感谢两位朋友凌晨一起讨论问题
@BeyondLimits
@thorn
