Task.1 投票
题目大意：有 \(n\) 个同学投票，每个人有一个投赞成票的概率 \(p_i\)。现在要从中选出 \(k\) 个同学，使得这 \(k\) 个人投票的平票的概率最大。
数据范围：\(1\leq N,K\leq 2000\)
考场上自己生成数据找规律发现一定是对所有人的 \(p_i\) 排序后头尾各取几个人（可以不取），做 \(O(N^2)\) DP 拿到了 \(70\) 分。这个性质的正确性具体来说就是假设已经确定了一些人，再选一个人结果是关于选的这个人的 \(p\) 的一个一次函数（其他部分已经确定，为常数）。具体推导可以看：here。利用这条性质，我们只需要对前缀后缀各 \(O(N^2)\) 做一遍DP算出概率再 \(O(N)\) 枚举前面选几个人即可。复杂度 \(O(N^2)\)。
代码：
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
typedef double db;
const int N=2005;
int n,k;
db p[N],c[N],f[N][N],g[N][N],ans=0;
int main(){
freopen("vote.in","r",stdin);
freopen("vote.out","w",stdout);
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)scanf("%lf",&p[i]);
sort(p+1,p+n+1);
for(int i=n-k+1;i<=n;i++)c[n+1-i]=p[i];
f[0][0]=g[0][0]=1.0;
for(int i=1;i<=k;i++){
for(int j=0;j<=i;j++){
f[i][j]=f[i-1][j]*(1.0-p[i]);
if(j>0)f[i][j]+=f[i-1][j-1]*p[i];
g[i][j]=g[i-1][j]*(1.0-c[i]);
if(j>0)g[i][j]+=g[i-1][j-1]*c[i];
}
}
for(int i=0;i<=k;i++){
db tmp=0;
for(int j=0;j<=k/2;j++)tmp+=f[i][j]*g[k-i][k/2-j];
ans=max(ans,tmp);
}
printf("%lf\n",ans);
return 0;
}
Task.2 动态数点
题目大意：对于一个数列 \(a\)，如果一段区间 \([l,r]\) 中存在 \(a_k\) 满足 \(\forall\ i\ a_k|a_i\)，这段区间的价值就是 \(r-l\)。给出序列 \(a\)，求出所以区间中最大的价值以及哪些区间价值最大。
数据范围：\(1\leq N\leq 5\cdot 10^5,1\leq a_i\leq 2^{32}-1\)
存在不止一个 \(O(N\log N)\) 的解法，比如预处理一个区间 \(gcd\) 的ST表，然后对于每一个位置考虑能不能作为 \(a_k\)，向左向右拓展，比较区间 \(gcd\) 是否是它的倍数。
这里给出一种 \(O(N)\) 的解法：先从小到大枚举作为 \(a_k\) 向右边能拓展到的最远距离，这个时候这段距离中经过的点一定不会比当前的点更优，然后在倒着向左边做同样的事情，在这个过程中记录和更新答案即可，因为操作顺序的缘故，得到的答案也是有序的。
代码：
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
template<class T>void read(T &x){
x=0; char c=getchar();
while(c<'0'||'9'<c)c=getchar();
while('0'<=c&&c<='9'){x=(x<<1)+(x<<3)+(c^48); c=getchar();}
}
typedef long long ll;
const int N=500050;
int n;
ll a[N];
int left[N],right[N],len=-1,p[N],tot;
int main(){
freopen("point.in","r",stdin);
freopen("point.out","w",stdout);
read(n);
for(int i=1;i<=n;i++) read(a[i]);int l,r; ll t;
for(int k=1;k<=n;){
r=k; t=a[k];
while(r<n&&a[r+1]%t==0)++r;
right[k]=r; k=r+1;
}
for(int k=n;k;k--)if(right[k]){
l=k; t=a[k];
while(l>1&&a[l-1]%t==0)--l;
left[k]=l;
}
for(int i=1;i<=n;i++){
if(right[i]-left[i]>len){
len=right[i]-left[i];
p[tot=1]=left[i];
}
else if(right[i]-left[i]==len)
p[++tot]=left[i];
}
printf("%d %d\n",tot,len);
for(int i=1;i<=tot;i++)printf("%d ",p[i]); puts("");
return 0;
}
Task.3
题目大意：
数据范围：
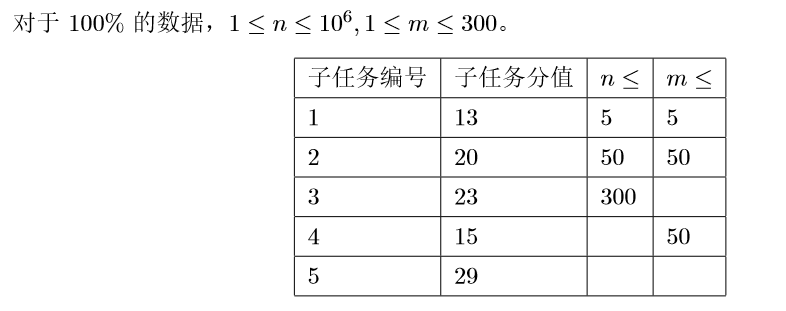
正解 DP，非常有趣但是我没完全理解，坑待填。
