今天早上终于把一直卡着的那道整完了,心情舒畅。但是马上就发现还有好些东西没学。写了一上午splay和treap博客的草稿了,趁热写下网络流的博客好了,就当换个脑子。
为什么是23呢?因为机器人路径规划问题我不会啊嘿嘿。
Pt.1 关键词统计
好像没什么用,但是这些东西还是和网络流有点联系的好
最多 最大 最长 最小 最少(短)
数量 收益 长度 总和 花费 路线 耗时
方案
数据范围 10 20 100 500
Pt.2 模型
1) 二分图
对应问题:最大匹配,最小点覆盖,最小边覆盖,最大独立集,最大权独立集
①:最大匹配(及多重匹配)的最大流模型
对第一个集合中的元素向源点连边,容量为1
对第二个集合中的元素向汇点连边,容量为1
对于两个集合中相连的点连边(S1->S2),容量为1
求最大流。正确性如下
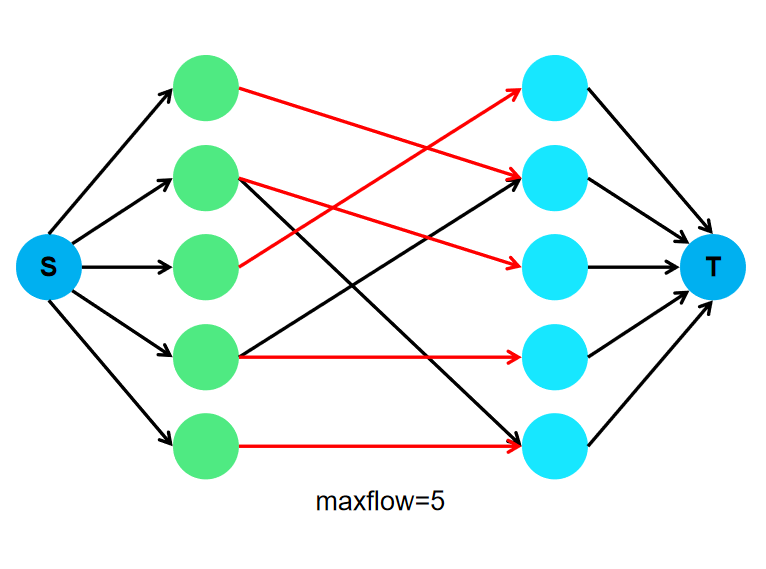
此外,使用dinic,EK算法还可以利用残量网络的特点求出具体哪些边是匹配边和其端点,解决了输出方案的问题
1.飞行员配对方案问题
本题是一个非常明显的二分图模型,求最大匹配并且输出方案。
输出方案时,判断残量网络中所有正向边流量为0或判断反向边流量为1表明在最终方案中这条边是匹配边。
5.圆桌问题
【多重匹配】
从源点向国家连容量为国家代表数的边,国家和桌子间连容量为1的边,桌子到汇点连容量为桌子人数的边。求最大流。
7.试题库问题
同上
18.分配问题【费用流出现了QAQ】
不考虑效率人和工作的关系是一张二分图,并且题目保证存在一个完美匹配(所有的活都有人干)。加上效率,求的就是所有活都有人做的时候(最大流哇)最大的效率,即最大费用最大流。
②:最小点覆盖的最大流模型
最小点覆盖是一个覆盖了所有的边的点集
最小点覆盖=最大匹配数
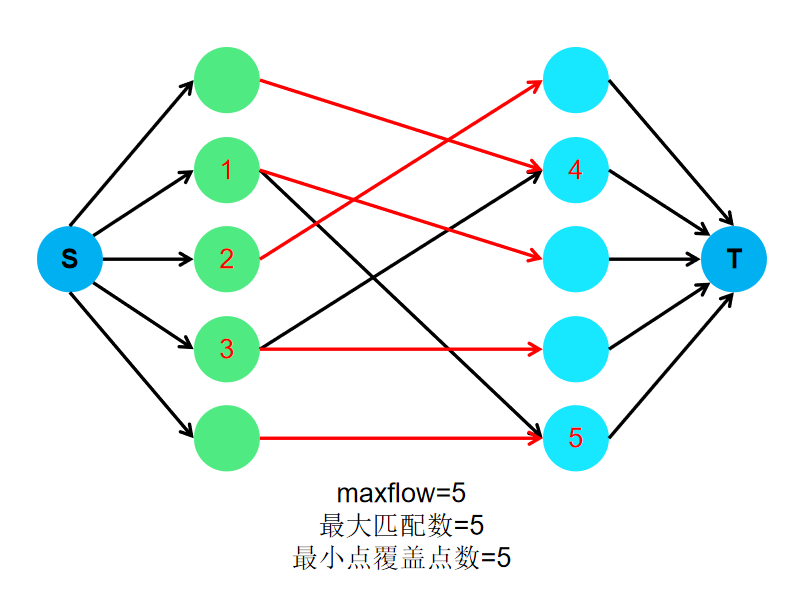
证明:反证法,用上面那张图。
匹配边的端点至少有一个端点连接非匹配边。
如果存在一条非匹配边边不被匹配边的端点覆盖,这条边就是匹配边,因为其端点还为被匹配。
所以匹配边的端点集是一个点覆盖集(匹配数*2),同时两条匹配边的端点如果是一条非匹配边的端点,那么只需要其中一个端点就能覆盖。所以所有匹配边的的一个端点组成最小点覆盖集,大小为匹配数(最大匹配数)。
诶,24题中好像没有这类题,下一个下一个。
③:最大独立集/最大权独立集
独立集是一个点集,所有的点都不相连。
最大独立集=点数-最小点覆盖=点数-最大匹配数
最大权独立集=点权和-最小割容量=点权和-最大流(这个暂时我没有想出来证明,胡伯涛前辈的论文中有详细介绍)
24.骑士共存问题
自习读题后发现棋盘上的黑白格不能共存,他们是否满足二分图的性质呢?答案是肯定的。那么我们要求的就是互不相邻的最大骑士个数,即最大独立集。
9.方格取数问题
发现了么,二分图的模型。还是黑白格,但是有了权值,求最小割(最大流),利用上面的结论。
2) 标准的费用流模型
值得注意的是,EK+spfa/EK+dijkstra中的费用是单位费用,切勿在建模时和边权混淆。
10.餐巾计划问题
模型很明显,为了区分用过的餐巾和干净餐巾,我们把每一天拆开,入点<x,i>接受干净餐巾,出点<y,i>接受<x,i>和其他来源的用过的餐巾。再额外建立快慢洗店。求最小费用最大流。
17.运输问题
模型非常明显,不多言。
19.负载平衡问题
环?没法贪心呀。如果知道这题网络流可做,模型非常容易建立(问题是考试时候我怎么知道)。
20.深海机器人问题 & 23.火星探险问题
按照题目要求建好图,跑就行了,嘿嘿嘿。
3) 隐藏的模型(好题好题)
【最大流】
6.最长递增子序列问题
3个子任务,Task1没啥问题,Task2怎么做呢?
Task1在DP完了之后,数组f中存在一些重要信息,这些信息中存在f的转移关系。F[i]=maxlen从f[j]=maxlen-1转移来,f[j]=maxlen-2从f[k]=maxlen-3转移来...f[x]=1。如果我们把这个关系拎出来,就找到了一个最长上升子序列,如果可以拎出来更多组关系,就找到了其他的子序列。从f[i]=1传递到f[j]=maxlen,这些关系恰构成一个网络,其中的最大不相交路径条数就是子序列个数,其最大流就是子序列个数。
11.航空路线问题
题意求最大环。So?真的是网络流吗?起点到终点存在一条路径时就有解。设立源点连到起点,汇点到终点,容量均为2。城市间连边,容量为1。跑最大费用最大流。流量为0无解,1有去无回,除法起点知道直连,2输出方案。
16.数字梯形问题
诶?这个图有点像上面最长递增子序列问题?没错,又是一道不相交路径,不过有了权值。
21.最长k可重区间集问题 & 22.最长k可重线段集问题
终于到了24题中非常喜欢的几道了!
这道题怎么读,和网络流有个啥关系???我2^n枚举集合?解析几何?
操作了一波发现没什么好方法啊?网络流!
这个k,好k哇。想想最后那个k可重集的组成,一定是不超过k个不重集构成,nice!有点头绪了,不重集...不重集...不相交...不相交路径???喔,有点东西了。

区间集是这样吧
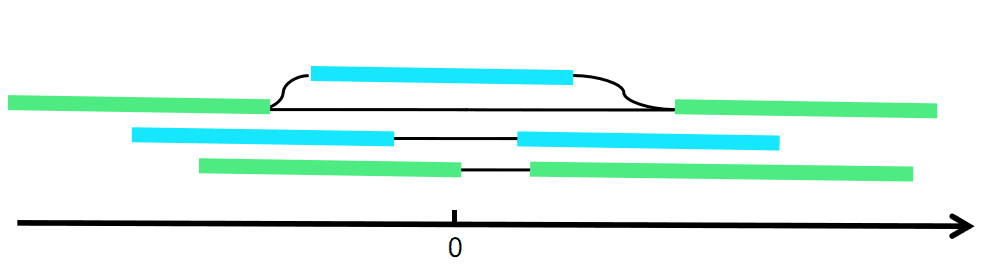
我们把不相加的连起来,诶!
跑最大流即可。
线段集的坑点:垂直!
4) DAG的最小路径覆盖 & 2道妙题
最小路径覆盖=点数-最大匹配数
这个东西,呃怎么证啊...
3.最小路径覆盖问题
题如其名,最大流,结论求解。
4.魔术球问题
非常棒的一道题。有一种非常厉害的贪心解法,可惜我想不到。
其次这道题连个图都没有!我们再动手。...好像不太好画啊。
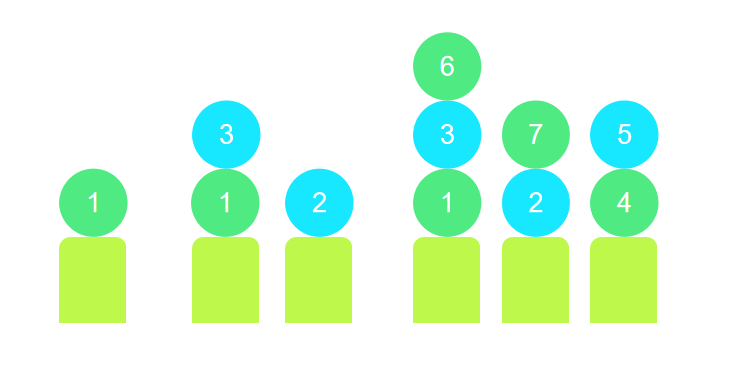
我们发现,每增加1个球结果可能会改变上一次的球的结构,增加新的柱子。除非我们知道答案,否则是无法决定下一步加什么球的。数字和数字间连边,数字和柱子间连边,每根柱子上的球不能重复,有感觉了吗?n根柱子不是n条不相交路径吗?反过来问你最大点数。所以先确定枚举点数,确定点数后,再跑最大流求最小路径覆盖,和n比较,直到最大流超过n,此时得到了答案。
2.太空飞行计划问题
再次推荐胡伯涛前辈的论文,该题模型为最大权闭合子图,求最小割,答案为总和-最小割容量。
13.星际转移问题
卡我最久的一道,首先这个图怎么建我想了快一周!最后还是看的题解。
因为每一天飞船的位置都在变化,边是变化着的,运用一个分层图的思想可以让事情变得明了:

枚举天数,每增加一天就增加一层图,看看最大流有没有超过人数,超过了就输出天数。
5) 披着狼皮的羊
以下几道题网络流都不是最优解法(虽然以上也有些是)
其名曰:分层图最短路。
当我们发现地图不停变化时,不妨按照某个状态划分出若干个地图,在其中解决问题,这个时候费用流和最短路相比就显得相形见绌了。(推荐肖天前辈2004的论文)
12.软件补丁问题
14.孤岛营救问题
15.汽车加油行驶问题
这三道题数据范围都较小,对于12.中的软件修复状态,14.中的钥匙状态,15.中的行驶里程都可以用二进制数存储,然后在n^2*(1<<k)的图中求最短路。
最后感谢byvoid前辈的题解及数据,洛谷的部分题解,和几位前辈的论文。
若发现本博客有何错误或不妥,请指出。
转载请注明出处。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号