PlaneGCS-平面几何约束求解器用法

PlaneGCS-平面几何约束求解器用法

eryar@163.com

1 Introduction

在传统的机械设计软件中，一般使用几何约束求解器来画草图，再通过对草图进行拉伸旋转等生成特征实现建模功能。基于参数化历史特征方式来建模的软件绕不开几何约束求解器，目前主流商用软件一般使用西门子D-Cubed DCM及达索的CGM。开源世界也有两款几何约束求解器：SolveSpace和PlaneGCS。

PlaneGCS字面意思是平面几何约束求解器，主要用于绘制二维草图。因为PlaneGCS代码相对清晰，功能简单，只能处理平面几何元素的约束，本文主要结合示例代码介绍PlaneGCS的使用方法，在会用的基础上去理解源码的实现逻辑。

2 PlaneGCS

PlaneGCS主要包含三部分：

• 几何元素数据结构文件：h/Geo.cpp
• 约束条件文件：h/Constraints.cpp
• 约束求解实现文件：h/GCS.cpp

其中几何元素数据结构中定义的几何元素如下图所示：

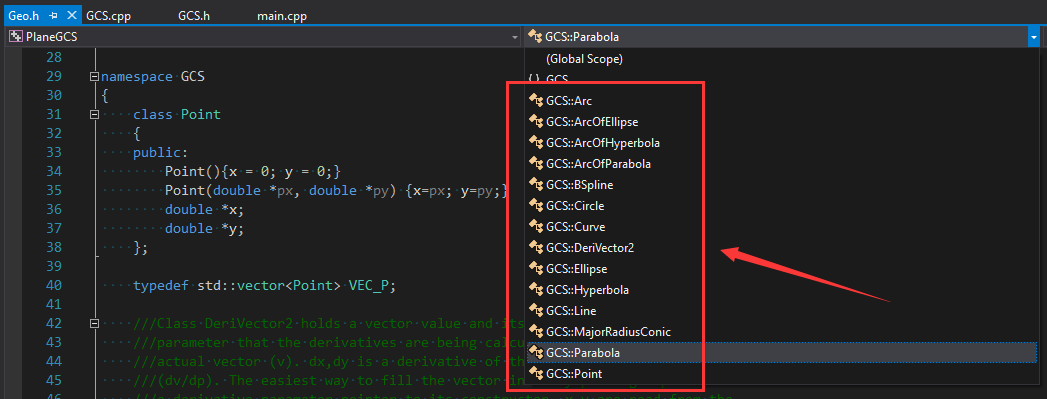
从上图可以看到，目前支持的几何元素有点Point，直线Line，圆Circle，椭圆Ellipse，双曲线Hyperbola，抛物线Parabola，圆弧Arc/ArcOfEllipse/ArcOfHyperbola/ArcOfParabola，及B样条曲线BSpline，不过看代码BSpline部分函数没有实现，应该是不支持的。

约束条件文件定义的约束类型如下图所示：

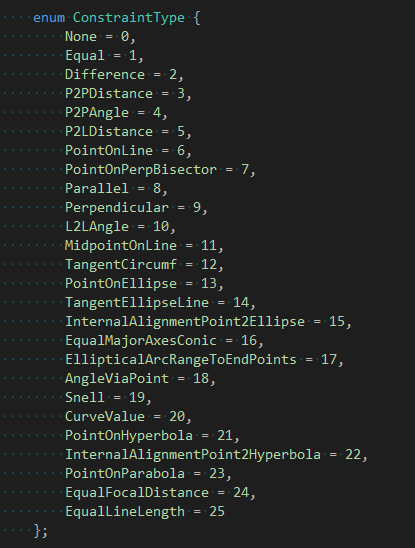
从约束求解文件中可以看到，其中数学计算主要使用Eigen中非线性方程组求解算法和boost的图graph算法，从中可以推测出实现平面几何约束求解器中需要的关键技术。先掌握PlaneGCS的用法，然后再分析其背后的实现原理细节。

3 Code Example

这里给出一个简单的示例程序，先让大家对PlaneGCS有个认识。示例程序中演示了给两条直线加上水平和垂直约束。为了便于查看约束后的结果，在代码中生成Draw Test Harness脚本文件。

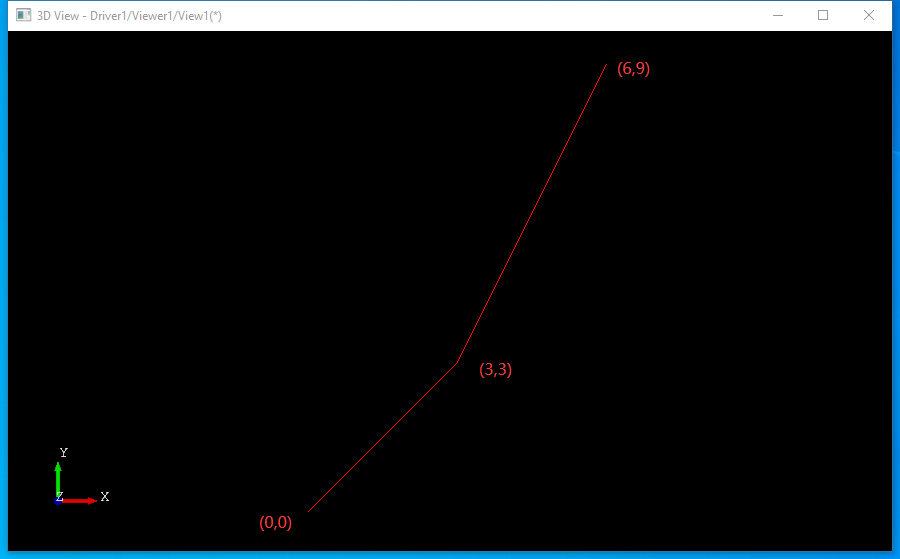
程序代码如下所示：

/*
Copyright(C) 2023 Shing Liu(eryar@163.com)

Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files(the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and / or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions :

The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT.IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.
*/

#include "GCS.h"

#include <fstream>

void test()
{
    double aPx1 = 0.0;
    double aPy1 = 0.0;
    double aPx2 = 3.0;
    double aPy2 = 3.0;
    double aPx3 = 6.0;
    double aPy3 = 9.0;

    GCS::VEC_pD aParameters;
    aParameters.push_back(&aPx1);
    aParameters.push_back(&aPy1);
    aParameters.push_back(&aPx2);
    aParameters.push_back(&aPy2);
    aParameters.push_back(&aPx3);
    aParameters.push_back(&aPy3);

    GCS::Point aP1(&aPx1, &aPy1);
    GCS::Point aP2(&aPx2, &aPy2);
    GCS::Point aP3(&aPx3, &aPy3);

    GCS::Line aLine1;
    GCS::Line aLine2;

    aLine1.p1 = aP1;
    aLine1.p2 = aP2;

    aLine2.p1 = aP2;
    aLine2.p2 = aP3;

    std::ofstream aTclFile("d:/gcs.tcl");
    aTclFile << "# 2 lines before PlaneGCS solve" << std::endl;
    aTclFile << "vinit" << std::endl;
    aTclFile << "vertex aP1 " << aPx1 << " " << aPy1 << " 0" << std::endl;
    aTclFile << "vertex aP2 " << aPx2 << " " << aPy2 << " 0" << std::endl;
    aTclFile << "vertex aP3 " << aPx3 << " " << aPy3 << " 0" << std::endl;
    aTclFile << "polyvertex aPolyline1 aP1 aP2 aP3" << std::endl;
    aTclFile << "vdisplay aPolyline1 " << std::endl;
    aTclFile << "vsetcolor aPolyline1 RED" << std::endl;

    GCS::System aSolver;
    aSolver.addConstraintHorizontal(aLine1);
    aSolver.addConstraintVertical(aLine2);

    if (aSolver.solve(aParameters) == GCS::Success)
    {
        aSolver.applySolution();

        aTclFile << "# 2 lines after PlaneGCS solve" << std::endl;
        aTclFile << "vertex aV1 " << aPx1 << " " << aPy1 << " 0" << std::endl;
        aTclFile << "vertex aV2 " << aPx2 << " " << aPy2 << " 0" << std::endl;
        aTclFile << "vertex aV3 " << aPx3 << " " << aPy3 << " 0" << std::endl;
        aTclFile << "polyvertex aPolyline2 aV1 aV2 aV3" << std::endl;
        aTclFile << "vdisplay aPolyline2 " << std::endl;
        aTclFile << "vsetcolor aPolyline2 GREEN" << std::endl;
    }

    aTclFile.close();
}

int main(int argc, char* argv[])
{
    test();

    return 0;
}

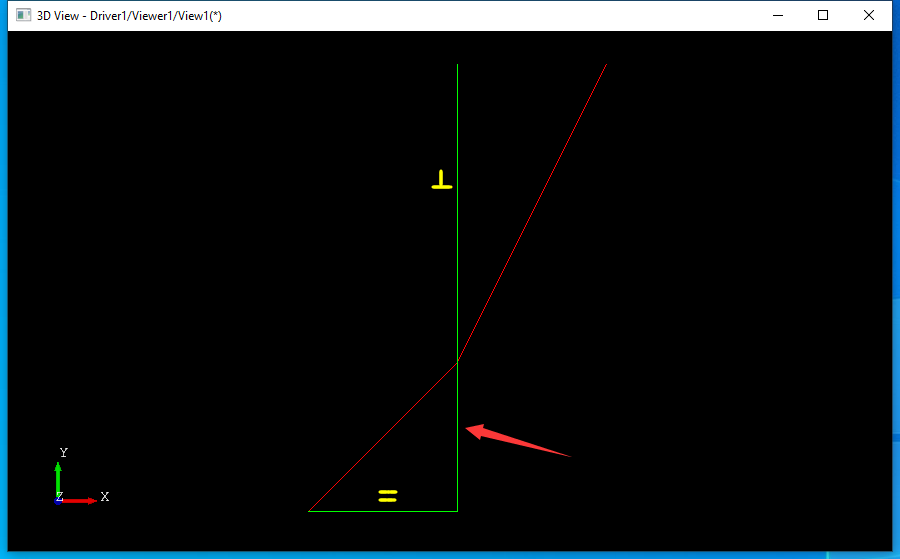
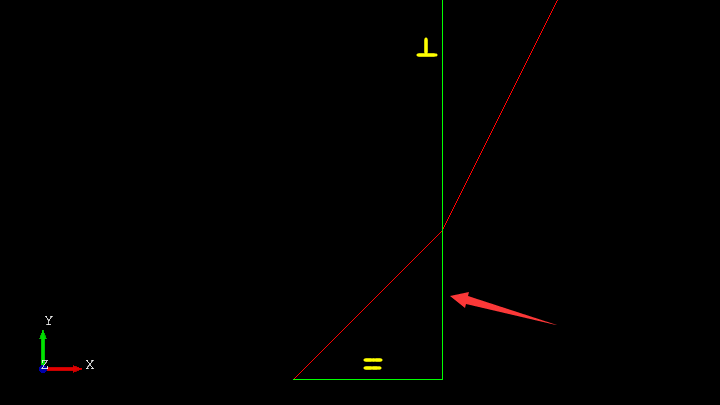
从程序代码中可以看出PlaneGCS的使用先要定义需要计算的参数aParameters，这些参数是几何元素中的数据，都是使用的指针。然后将约束加入到GCS::System中，最后代入参数调用solve函数进行求解。求解成功后使用applySolution()函数应用求解结果。求解结果在Draw中显示的绿色的线如下图所示：

4 Conclusion

本文结合示例代码演示如何使用PlaneGCS，主要使用了水平和垂直约束。PlaneGCS中还支持其他约束类型，童鞋们可以自己探索一下。几何造型内核和几何约束求解器常被看作是工业CAD软件的卡脖子技术，开源库一般功能不太完善，但是用来探索背后的实现原理还是有参考借鉴意义的。希望有更多的童鞋去了解背后的原理，共同来提高国内三维CAD软件开发水平。