几何内核与数学

几何内核与数学

1 概述

从1950年第一台图形显示器（美国麻省理工大学MIT旋风I号Whirlwind I）的诞生，到1962年MIT林肯实验室的Ivan E. Sutherland发表题为“Sketchpad: 一个人机交互的图形系统”确定计算机图形学作为独立科学分支。经过70多年的发展，计算机图形学中的几何造型技术成了现在的几何内核。

数学是我们从小学、中学到大学一直都在学习的课程，是现代科技的理论基础，是创新的源泉。几何内核与数学的联系非常紧密，结合开源几何内核opencascade谈谈学习过程和数学的认识。

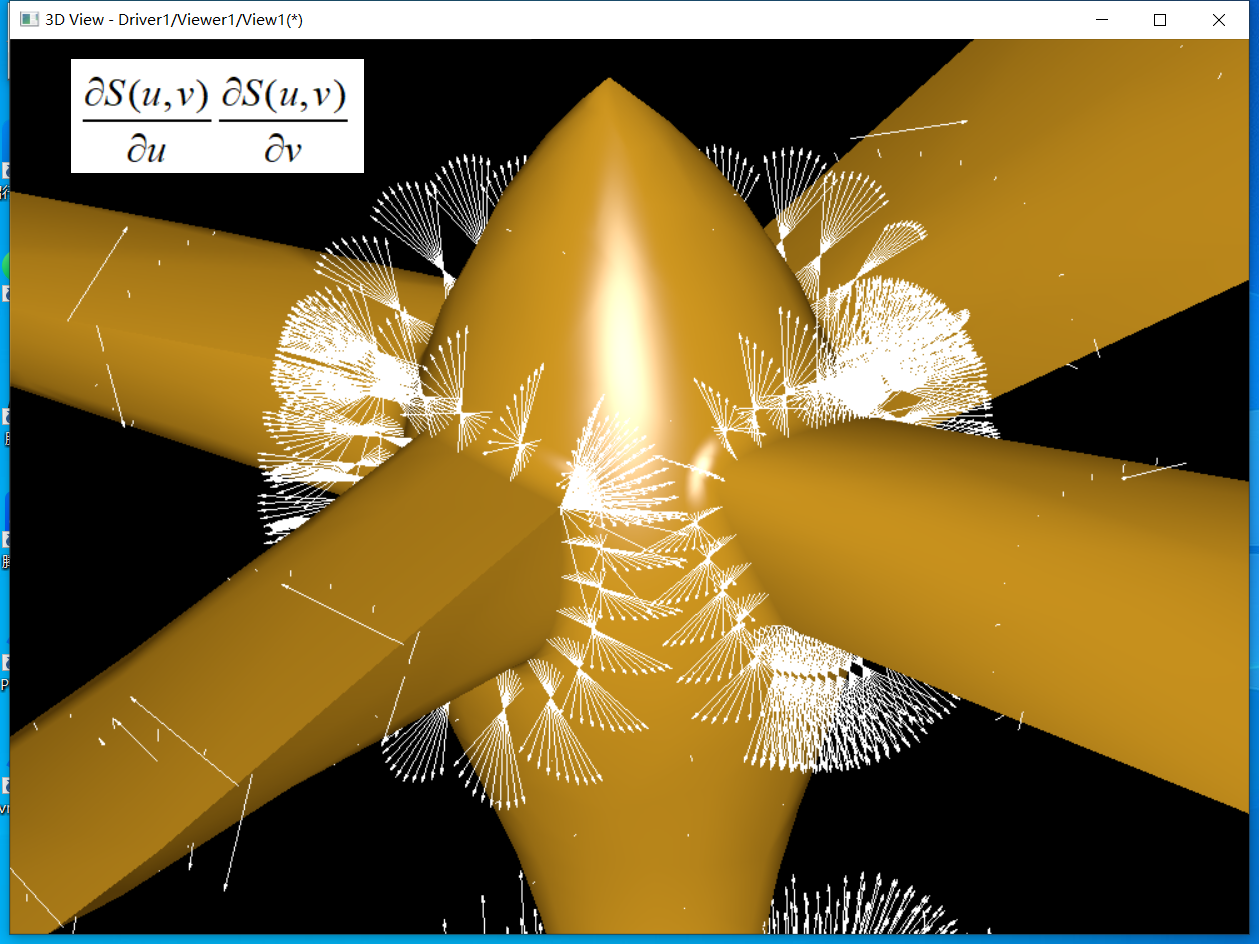
2 高中时代

在刚学习的时候，总是先从简单的开始入手。比如，先看看直线、圆是什么，怎么显示出来。长方体、圆柱体等怎么用BREP进行表示，怎么显示在屏幕上。这个时候考虑问题是常人思维，我认为是高中时代。

比如，怎么计算二维直线与圆的交点呢？上过高中的都学过，联立直线与圆的一元二次方程组，将解方程组的代码固化在代码中。当计算椭圆与圆的交点时，也做同样的处理，就是多写点代码。高中几何学得好的，可能会说我可以用向量，向量的方法会比代数的方法速度要快。

再比如，怎么计算曲线的弧长和曲面的面积呢？计算曲线可以通过对曲线进行采样点，将点连成多段线，再分别计算每小段线段的长度累加就是了。面积咱们也可以类似处理，将曲面离散成三角形或四边形，再将这些三角形或四边形面积累加。这些方法都能实现，但是性能、精度都会成为问题。要计算得精度高，采样就要密，就会带来性能问题。

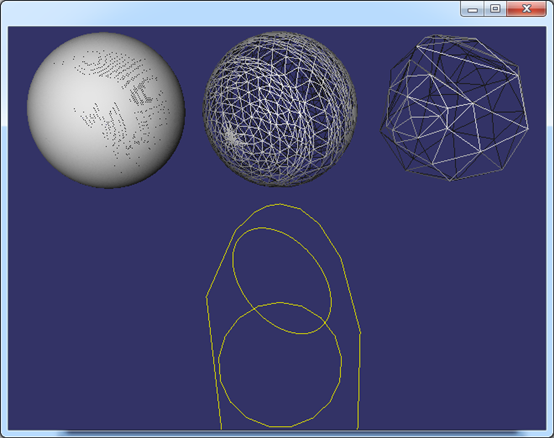
3 大学时代

到了大学时代学习过高等数学、线性代数等，有了更有力的工具来解决更一般问题。面向对象编程和数学也是相通的，就是将问题抽象的能力。这个时候眼中没有直线、圆、B样条曲线、平面、球面、B样条曲面等等，只有线Curve和面Surface。

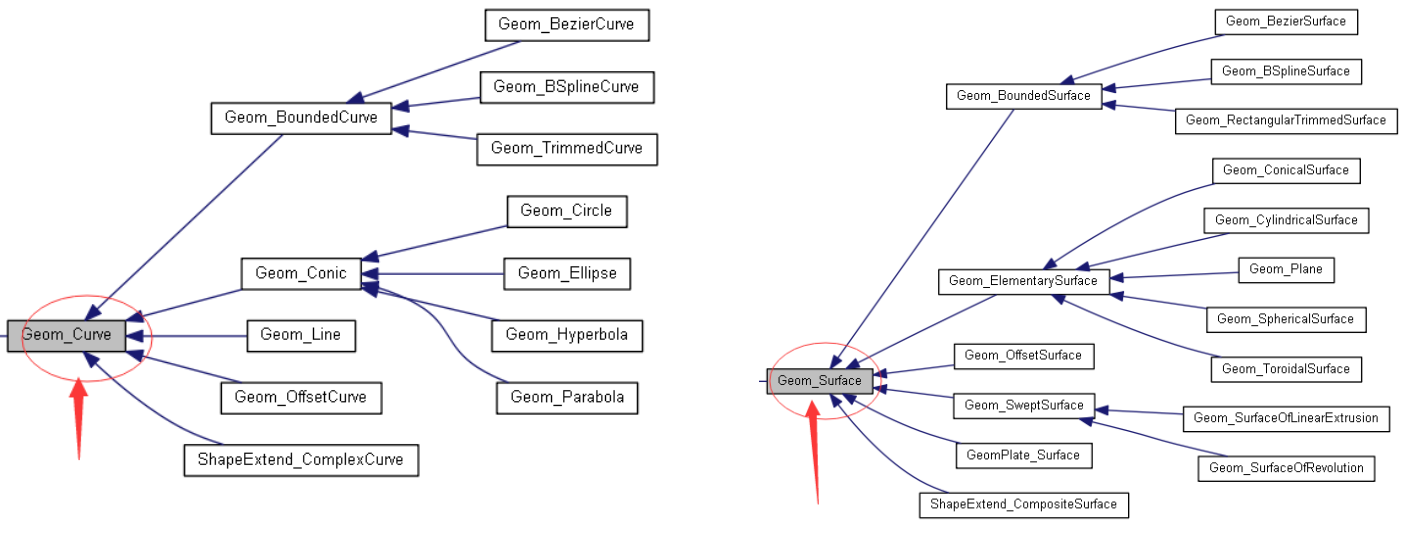
再进一步抽象，将线Curve与一元函数F(x)对应，将面Surface与多元函数对应F(x,y)，与数学建立了联系。

这时就可以使用数学工具对问题进行处理了。如计算曲线弧长，就变成一个对切向量的积分。曲线切向量需要计算一阶导数，《The NURBS Book》等书上计算B样条微分的公式就有用，看待B样条曲线和看待圆一样了。

积分的计算可以使用数值方法，如Newton-Cotes或Gauss积分法，使用更少的迭代获得更高的精度，程序优化的方向也清晰。

 

从opencascade的类math_Function和math_MultipleVarFunction可以可以看出，许多几何问题都抽象成了数学问题。有很多人问我，怎样才算入门了opencascade呢？那就是思考问题的方式转换成数学的方式，我觉得就算入门了。再具体点可操作点呢，首先就是数据结构的入门，掌握BREP边界表示法，如在圆柱面Surface上框出一个小面片Face，能正常显示出来就算理解opencascade中的BREP结构。其次是几何算法入门，就是将从math_Function和math_MultipleVarFunction所有的派生类的数学公式写出来。这两点动手做完，我觉得可以算入门了。

 

4 研究生时代

如果大学时代我们掌握了微分、积分、线性代数，到研究生时代应该掌握变分、偏微分方程、最优化理论等等。如偏微分方程用于构造过渡曲面，曲线曲面拟合光顺最后都抽象成带约束的非线性方程组的求解。

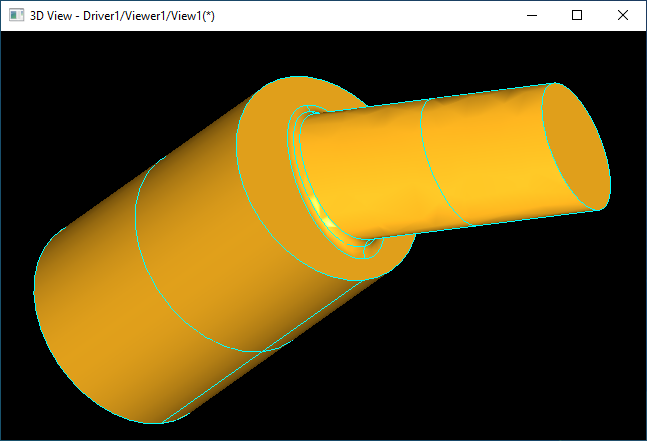
到研究生时代因为掌握的数学工具，会处理看上去很简单但处理起来更复杂的问题：如上图所示的过渡Blend，以及蒙面Skinning和扫掠Sweep等。

这时也可以有一些智能算法，如遗传算法、蚁群，粒子群PSO优化算法，AI等，使用仿生、遗传变异等手段使求解迭代更快收敛。为传统优化算法提供初始解，使传统算法能更快、更准地找到解析解，不至于深陷局部最优解中不能自拔。在opencascade中也有相关实例，如math_PSO。这些智能算法有随机性，不像解析算法那样满足一定约束条件必定会找到相对准确答案。只能作为像曲面求交之网格离散法，作为参数迭代法的预处理。到这个时代，查看相关技术论文毫无压力，面对一般的几何问题都应该可以从容应对。和研究生一样面对的问题更加具体，会钻牛角尖。

5 总结

综上所述，几何内核可以看成一个数学库的子集，只是在几何图形上的应用。学习几何内核的过程类比于学生时代掌握的数学工具。在高中时代，看问题很具体，只能case by case的处理，功能能做出来。到大学时代，有了一定的抽象能力（与面向对象编程一样），看问题具有一般性，能使用更高级点的数学工具来处理，有能力来兼顾精度和性能。到了研究生时代，就不怕别人来卡脖子，甚至能超越别人。这个时候不要给自己设限，找准喜欢的方向去钻牛角尖，终会有所成。