OpenCASCADE Point Classifier
OpenCASCADE Point Classifier
在解决几何问题时常会遇到这样的问题：给定平面上一个有N条边的简单多边形P和一点z，在问点z是在P的内部还是外部，或者是在多边形的边上。在OpenCASCADE中也有对点的位置判断的功能，叫分类器Classifier，其主要功能就是用于点的定位。点定位功能主要用于模型的网格化Mesh，布尔运算（BO）中面的重构等。
点定位的状态由TopAbs_State来表示，总共有以下几种状态：
引入UNKNOWN是因为这个枚举也经常用于表示计算失败的状态。当不能确定点在外部或内部时，就用UNKNOWN来表示。
点定位相关的类名都是带有Classifier或其缩写，如：
l CSLib_Class2d：最底层的多边形点定位类，用于二维空间点与多边形的定位；
l BRepClass_FaceClassifier：判断参数点是否在面Face的参数空间和模型点是否在面上；
l BRepClass3d_SolidClassifier：判断点是否在体Solid内部；
l IntTools_FClass2d：判断参数点是否在面Face的参数空间；
判断一个点是否在多边形内部常见算法有：
（1）面积和判别法：判断目标点与多边形的每条边组成的三角形面积和是否等于该多边形，相等则在多边形内部。
（2）夹角和判别法：判断目标点与所有边的夹角和是否为360度，为360度则在多边形内部。
（3）引射线法：从目标点出发引一条射线，看这条射线和多边形所有边的交点数目。如果有奇数个交点，则说明在内部，如果有偶数个交点，则说明在外部。时间复杂度：O（n） 适用范围：任意多边形。是非常不错的算法（不需考虑精度误差和多边形点给出的顺序），可以作为第一选择。算法思想：以被测点Q为端点，向任意方向作射线（一般水平向右作射线），统计该射线与多边形的交点数。如果为奇数，Q在多边形内；如果为偶数，Q在多边形外。
OpenCASCADE中判断点在多边形内部也是采用了射线法，相关代码如下：
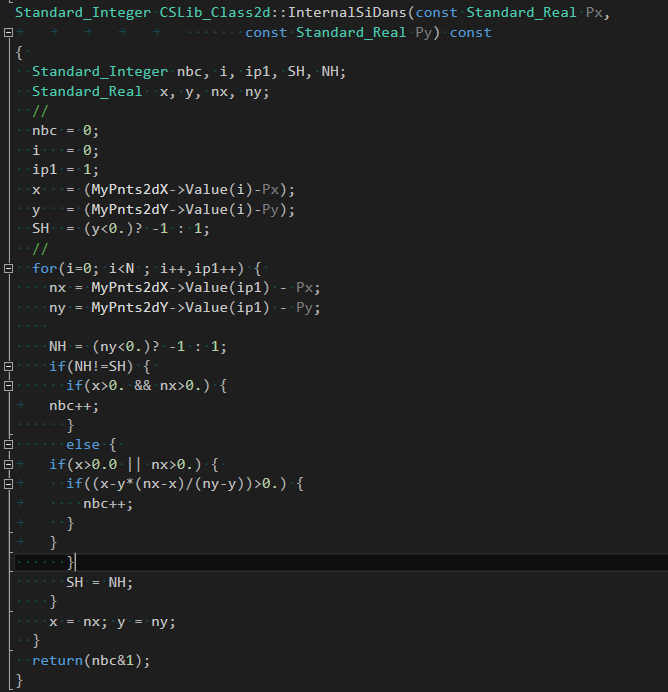
其中变量nbc即是交点的个数。
x, y是需判定点与多边形中一条线段起点的差值，SH是表示点与起点的状态，起点在判定点下方时为-1，否则为1；
nx, ny是需判定点与多边形中一条线段终点的差值，NH是表示点与终点的状态，终点在判定点下方时为-1，否则为1；
当多边形中一条线段起点和终点与指定点状态不一致时，即判定点在线段的Y之间才会有相交。
返回值使用了一个位运算来判断交点个数是否为偶数。
参考资料：
1 https://blog.csdn.net/WilliamSun0122/article/details/77994526
2 https://blog.csdn.net/zsjzliziyang/article/details/108813349
3 https://www.jianshu.com/p/0e974c27af09
为了方便大家在移动端也能看到我的博文和讨论交流，现已注册微信公众号，欢迎大家扫描下方二维码关注。
