OpenCASCADE 平面与球面求交

OpenCASCADE 平面与球面求交

eryar@163.com

 

OpenCASCADE提供了类IntAna_QuadQuadGeo用来计算两个二次曲面quadric（球面、圆柱面、圆锥面及平面，平面是二次曲面的特例）之间的交线。他们之间可能的结果有：

l 一个点

l 一条或两条直线

l 一个点和一条直线

l 圆

l 椭圆

l 抛物线

l 双曲线

 

将源码结合《高等数学》、《解析几何》等书，可以来学习如何将理论付诸实践。本文主要介绍这个类中平面与球面求交的源码实现。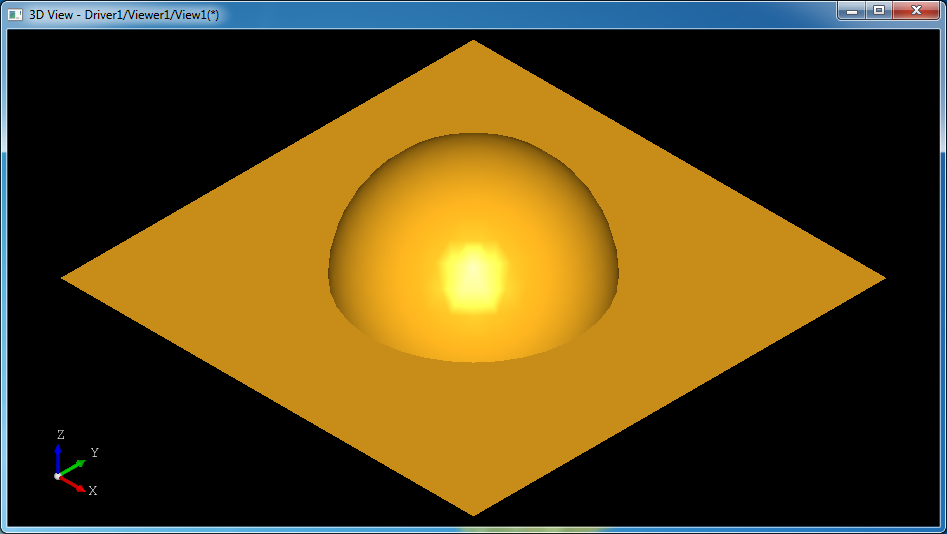 

将源码列出如下：

void IntAna_QuadQuadGeo::Perform( const gp_Pln& P
                                 ,const gp_Sphere& S) 
{
  
  done = Standard_False;
  Standard_Real A,B,C,D,dist, radius;
  Standard_Real X,Y,Z;

  nbint = 0;
// debug JAG : on met typeres = IntAna_Empty par defaut...
  typeres = IntAna_Empty;
  
  P.Coefficients(A,B,C,D);
  S.Location().Coord(X,Y,Z);
  radius = S.Radius();
  
  dist = A * X + B * Y + C * Z + D;
  
  if (Abs( Abs(dist) - radius) < Epsilon(radius)) {
    // on a une seule solution : le point projection du centre de la sphere
    // sur le plan
    nbint = 1;
    typeres = IntAna_Point;
    pt1.SetCoord(X - dist*A, Y - dist*B, Z - dist*C);
  }
  else if (Abs(dist) < radius) {
    // on a un cercle solution
    nbint = 1;
    typeres = IntAna_Circle;
    pt1.SetCoord(X - dist*A, Y - dist*B, Z - dist*C);
    dir1 = P.Axis().Direction();
    if(P.Direct()==Standard_False) dir1.Reverse();
    dir2 = P.Position().XDirection();
    param1 = Sqrt(radius*radius - dist*dist);
  }
  param2bis=0.0; //-- pour eviter param2bis not used .... 
  done = Standard_True;
}

理解上述代码需要有平面一般方程的概念及点到平面的距离计算公式：

 

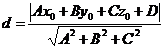
源码实现步骤如下：

l 取出平面一般方程的系数：A，B，C，D及球心坐标X，Y，Z；

l 计算球心到平面的距离dist；

l 若距离dist等于球面的半径，则平面为球面的切平面，只有一个交点；

l 若距离dist小于球面的半径，则平面与球面的交线为圆；

其中需要注意的是在获取平面一般方程的参数时，平面的法向为单位向量，所以在计算球心到平面的距离时的分母为1。

从上述代码可以看出OpenCASCADE的算法类的特点：即都有一个算法完成状态的函数IsDone()，通过成员变量done来设置，算法执行前都设置成false，算法成功后设置成true。还有一个前缀在变量名和函数名中很普遍，就是nb，是数量Number的缩写，这里是一个成员变量nbint，即相交的数量。