解析几何之二次型

解析几何之二次型

eryar@163.com

Abstract. 通过二次多项式的形式把二次曲线和二次曲面之间的求交问题统一成对将参数方程代入隐式方程得到问题的求解。

Key Words. Quadratic Form, Conic, Analytical Intersection

1. Introduction

二次型（quadratic form）：n个变量的二次多项式称为二次型，即在一个多项式中，未知数的个数为任意多个，但每一项的次数都为2的多项式。线性代数的重要内容之一，它起源于几何学中二次曲线方程和二次曲面方程化为标准形问题的研究。二次型理论与域的特征有关。

二次型是n个变量上的二次齐次多项式。下面给出一个、两个、和三个变量的二次形式：

 

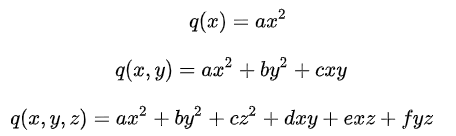
其中a, ...,f是系数。注意一般的二次函数和二次方程不是二次形式的例子，因为它们不总是齐次的，可能包含一次项和常数项。

几何造型中的圆锥曲线Conic Curve与二次曲面Quadric是一般的二次方程，方程分别为：

 

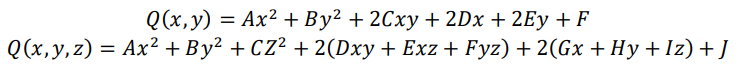
 在学习《线性代数》时也有关于二次型及其标准型的内容，在同济第四版《线性代数》书中这样写到“二次型及其标准型，这样一个问题，在许多理论问题或实际问题中常会遇到，现在我们把这类问题一般化，讨论n个变量的二次齐次多项式的化简问题。” 学这个有什么用啊？能解决哪些实际问题？下面我们看看二次型在实际问题中的应用。

2. Classification

在《工程技术中的偏微分方程》一书中，有二次型的一个应用，即对二次线性方程的分类Classification。我们从实际问题出发，可以推导并建立热传导方程，波动方程和Laplace方程，同时指出他们分别是抛物型、双曲型和椭圆型三类方程的典型代表。设有二阶线性方程

 

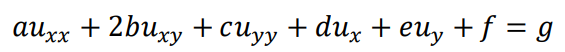
在解析几何中，XOY平面上的二次曲线方程的一般形式：

 

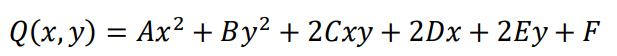
通过适当的坐标变换可以将上式化简成椭圆、双曲线和抛物线的标准方程，即对于任意二次圆锥曲线，都可以通过化成标准型的方法来判断圆锥曲线的类型。根据不同的类型，选择不同的求解方法。

 

3. Analytical Intersection

在《计算机图形学基础教程》书中有一章节“求交分类”，对几何曲线曲面求交进行了分析。摘录书中部分内容如下：

在几何造型中，通常利用集合运算（并、交、差运算）实现复杂形体的构造，而集合运算（布尔运算）需要大量的求交运算。如何提高求交的实用性、稳定性、速度和精度等，对几何造型系统至关重要。

在早期的几何造型系统中，用多面体来表示形体。在这种多面体模型中，形体所有的表面都是平面，所有的边都是直线段，因此求交计算主要是线段和平面的求交，求交问题的解决都相对简单。

但多面体模型的缺点是明显的。它只能近似表示形体。同时，复杂形体表面的离散会带来巨大的数据量，要求计算机有较高的存储量和运算速度。因此，有必要采用精确表示的形体模型，然而精确表示的形体也会给几何造型系统引入复杂的几何元素，也必然给几何元素的求交带来困难。

CSG模型是曾被广泛使用的形体表示模型，在这种模型中，形体通过基本体素的组合来实现，基本体素通常是立方体、圆柱、圆锥、球和圆环体等。基于CSG表示的造型系统，引入了二次曲面体和基本体素后，二次曲面的求交在这些造型系统中是不可避免的。

当前的几何造型系统，大多采用精确的边界表示BREP模型。在这种表示法中，形体的边界元素和某类几何元素对应，它们可以是直线、圆弧、二次曲线、Bezier曲线和B样条曲线等，也可以是平面、圆环面Torus、二次曲面、Bezier曲面和B样条曲面等，求交情况十分复杂。

对于含有两个变量的二次方程，对应的是二维二次圆锥曲线，在OpenCASCADE中的类gp_Circ2d, gp_Elips2d, gp_Hypr2d, gp_Parab2d, 他们都有一个函数Coefficients，能计算其二次型的系数。在解析几何曲线求交计算包中IntAna2d，提供了一个类IntAna2d_Conic用来表示圆锥曲线，类IntAna2d_AnaIntersection可以对这些圆锥曲线进行求交计算。

对于含有三个变量的二次方程，对应的是三维二次曲面，在OpenCASCADE中的类有gp_Pln, gp_Sphere, gp_Cylinder, gp_Cone, 他们也都有一个函数Coefficients，能计算其二次型的系数。在解析几何求交计算包中IntAna，提供了一个类IntAna_Quadric用来表示二次曲面。类IntAna_QuadQuad使用解析法（解方程）对两个二次曲面进行求交计算；类IntAna_QuadQuadGeo使用几何方法对两个二次曲面进行求交计算；类IntAna_ConicQuad用来对圆锥曲线和二次曲面进行求交计算。

3.1   二次曲线与二次曲线求交

二次曲线与二次曲线求交指的是用代数方法来计算两个曲线之间的相交情况，对应的类是IntAna2d_AnaIntersection。代数方法是利用代数运算，特别是求解代数方程的方法求解。由于圆锥曲线在其局部坐标系下具有标准的隐式方程和参数方程的噶啊，这类求交的策略是将坐标系变换到该圆锥曲线的局部坐标系下，一个圆锥曲线用隐式方程的形式表示，另一个圆锥曲线用参数方程的形式。对于曲线的参数方程而言，只有一个变量，将参数表示代入隐式方程即可获得一个变量的方程。occt中相关代码分析可参考：Intersection between 2d conic in OpenCASCADE

https://www.cnblogs.com/opencascade/p/6618865.html

 

 

3.2   二次曲线与二次曲面求交

二次曲线与二次曲面的求交计算，可以把二次曲线的参数形式代入二次曲面的隐式方程，得到关于参数的4次方程。然后用4次方程的求要公式计算出交点。occt中相关代码分析可参考：对应的类是IntAna_IntConicQuad

解析几何求交之直线与二次曲面

https://www.cnblogs.com/opencascade/p/IntAna_IntConicQuad.html

解析几何求交之圆与二次曲面

https://www.cnblogs.com/opencascade/p/IntAna_Circle.html 

3.3   二次曲面与二次曲面求交

二次曲面与二次曲面的求交计算，也可以把二次曲面的参数形式代入二次曲面的隐式方程。对应的类是IntAna_QuadQuad，其中对圆柱与二次曲面的求交计算源码注释如下图所示：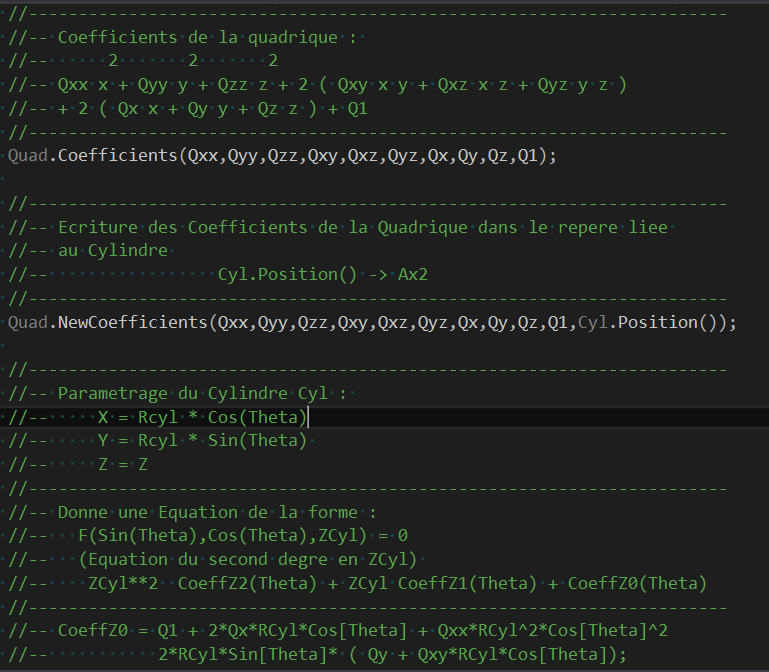 

3.4   二次曲面与二次曲面求交几何方法

几何方法求交是利用几何的方法，对参与求交的曲面的形状、位置以及方向等几何特点进行计算和判断，识别出交线的形状和类型，从而精确求出交线。对于一些交线退化或相切的情况，用几何方法可以更加迅速和可靠。在occt中对应的类是IntAna_IntConicQuad。关于源码分析可以参考：

OpenCASCADE 平面与球面求交

https://www.cnblogs.com/opencascade/p/PlaneSphere.html

OpenCASCADE 平面求交

https://www.cnblogs.com/opencascade/p/IntAna_PlanePlane.html

 

4. Conclusion

综上所述，通过二次多项式的形式把二次曲线和二次曲面之间的求交问题统一成对将参数方程代入隐式方程得到问题的求解。提供二次曲面几何求交算法，可以更快地得到结果。其实对于不包含B样条曲线曲面的模型（如CSG模型）来说，IntAna2d和IntAna已经可以实现求交，所以对于这些模型求交计算很快。

这也解决了我以前的一个疑问：为什么没有解析的三维圆锥曲线与曲线求交算法？因为三维圆锥曲线本身就是两个二次曲面的交线。没有像二维圆锥曲线和二次曲面那样有隐式方程。

5. References

5.1   同济大学数学教研室. 高等数学. 第四版 高等教育出版社

5.2   同济大学应用数学系. 线性代数. 第四版 高等教育出版社

5.3   潘祖梁, 陈仲慈. 工程技术中的偏微分方程. 浙江大学出版社

5.4   丘维声. 解析几何. 北京大学出版社

5.5   孙家广, 胡事民. 计算机图形学基础教程. 清华大学出版社