OpenCASCADE曲面求交之追踪法

OpenCASCADE曲面求交之追踪法

eryar@163.com

1 Introduction

朱心雄等著《自由曲线曲面造型技术》书中对曲面求交的追踪法（Marching method）有详细介绍，首先曲面求交追踪法的提出是1990年R.E. BARNHILL和S.N. KERSEY的一篇论文：A marching method for parametric surface/surface intersection感兴趣的可以下载来看看原文：

1990年我才几岁，那时家里有黑白电视机已经算不错的。对于一般NURBS曲面的求交，先用分割离散法求得交线的拓朴结构和交点的估计值，然后再应用迭代法根据估计值求得精确交点。如果认为交点分布不够细密，可以对网格进行加密，再应用迭代法得到新的精确交点，由此可以获得完整、致密的精确交线，而无需应用追踪法。

2 追踪法的原理

追踪法的原理：假设两曲面间共有N个交线环，先通过某种求交方法确定各交线环上的一个交点，然后以该交点为初始交点，根据交线的几何性质，按照一定步长计算该条交线上下一交点的近似值，再应用迭代法求得精确交点。沿交线走向不断前进，直到遍历整条交线。追踪法的优点是在求得首交点后搜索交线其余交点的速度非常快，且适用范围广。不论何种参数曲面，只要曲面不存在非正则点，并可以求得曲面上任意点的坐标位置、法矢、切矢等几何信息，就可以用追踪法求交。追踪法的问题是目前尚无非常有效的方法来求得所有交线环的起始点。在有些情况下寻求初始点所花费的时间远大于追踪法过程中所节省的时间，而为了节省寻求初始点的时间，又可能漏掉某些交线，当在孤立交点和比较小的交线环时尤甚。

3 追踪法的实现

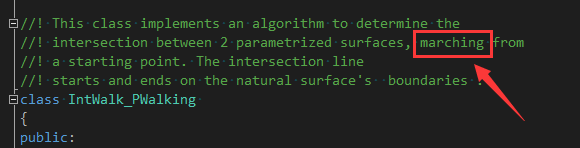
OpenCASCADE实现曲面求交追踪法的类是IntWalk_PWalking，注意看类注释中的单词marching:

追踪法中需要解决两个问题：

• 如何确定追踪方向：目前常用切线法确定追踪方向，即估计真实交线在该点的切线方向，并以此作为追踪方向。当曲面间存在切点时，由于在切点附近两曲面的法矢非常接近，无法确定追踪方向，这也就是所谓的“迷向”问题（Tangent tracks）。在类IntWalk_PWalking中，追踪方向作为成员变量tgdir，将迭代法计算的交线的切向量保存起来，当有“迷向”问题时，调用函数RepartirOuDiviser来修复。
• 如何确定追踪步长：追踪步长的选择通常有两种方法：1）固定步长和2）变步长也称为自适应步长法Adaptive Step。因为迭代法是根据估计点的参数来计算精确交点，为了避免根据点反求参数，直接根据切线方向的X,Y分量来确定参数的步长。虽然有些变化，总体上看使用的是固定步长法。若直接根据交线切线方向tgdir乘以步长得到点，是需要反求点在曲面上的参数。步长主要与精度设置有关，精度设置高，步长越小，则会导致计算速度慢，求出的交点过密，还可能带来不稳定因素。如步长过大，可能 会导致迭代不收敛或者跳到另外 一条交线上。

使用默认精度设置，追踪法得到的交点数量就很大。若设置精度低，交点数量会明显减少，提高计算速度。

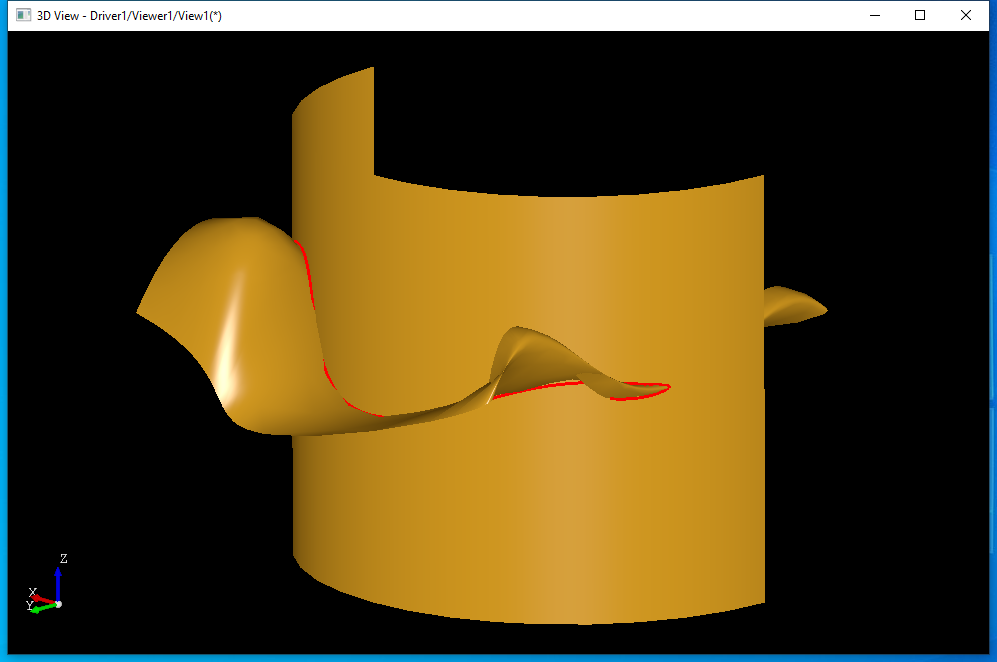
如上图所示，若两个曲面只有一个交线，使用有追踪法时只需要指定交线的初始交点，即可以得到整个交线。当两曲面有多个交线或有孤立交点时，就需要找出多个交线的起始交点：

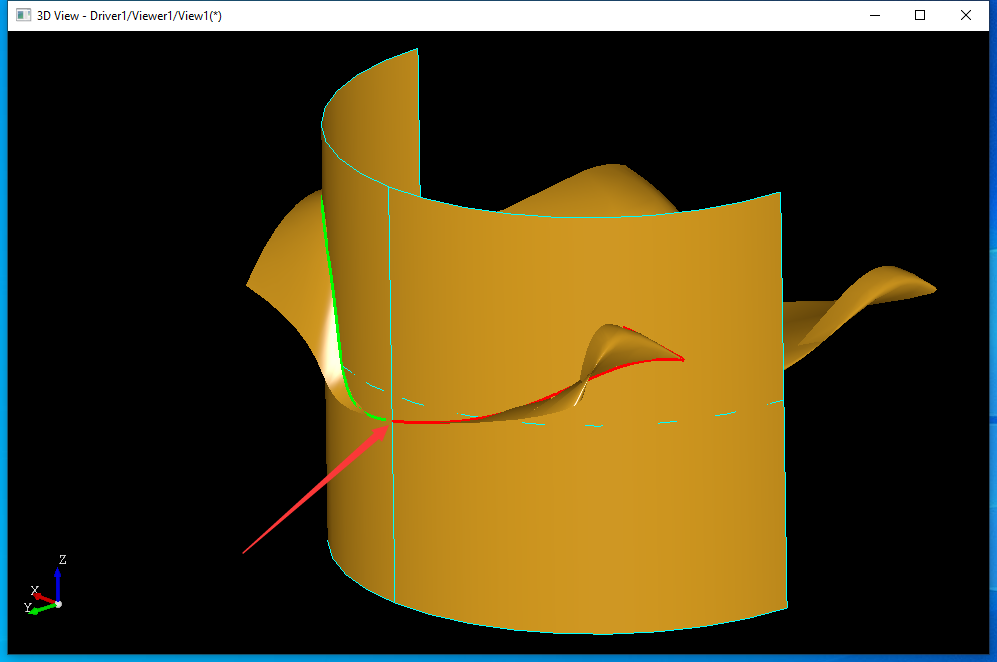
上图所示位置交线断开生成两条交线，一个是绿色一个是红色，这种情况就需要分别指出两个交线起始点。

4 Conclusion

综上所述，曲面求交追踪法的优点是在求得首交点后搜索交线其余交点的速度非常快，且适用范围广。追踪法的问题是目前尚无非常有效的方法来求得所有交线环的起始点。曲面求交一般会采用通用性较好的网格法-迭代法-追踪法三者相结合的方法。应用网格法求得交点的初始估计值，再用迭代法求得精确交点，并以其为起点进行追踪，直到得到整条精确交线。

IntWalk_PWalking追踪法的步长与精度密切相关，选择合适的精度，可以使交线的交点数量少，提高计算速度。因为精度越高追踪过程中得到的追踪点越多，对于每个追踪点都需要使用迭代法计算精确交点。