OpenCASCADE-曲面求交

OpenCASCADE-曲面求交

eryar@163.com

Abstract: 曲面求交是几何造型内核最为重要也最为复杂的问题之一，求交算法的质量（稳定、准确、快速）直接影响到几何内核的稳定性和实用程度，故具有十分重要的意义。求交问题包括曲线与曲线求交、曲线与曲面求交和曲面与曲面求交，其中最重要难度最大的当属曲面与曲面求交问题，其他求交问题可以应用曲面与曲面求交的思想予以解决。本文主要介绍opencascade中曲面与曲面求交的实现原理。

Key Words: Face Face Intersection, Intersection

1. Introduction

如果说理解opencascade中面的构造原理（即理解BRepBuilderAPI_MakeFace的源码），我觉得算是理解了BRep表示法的数据结构Modeling Data。如果说理解了曲面与曲面求交的实现原理，我觉得算是对几何内核中的核心算法布尔操作有了一定的认识。曲面与曲面求交过程（Intersection Algorithm）中主要依赖三大工具：拟合（Approximation Algorithm）、投影（Projection Algorithm）和定位（Classification Algorithm）。下面结合布尔操作TKBO中的曲面与曲面求交类IntTools_FaceFace源码实现分别介绍这三大工具的应用场景。opencascade中的算法类一般的使用套路和把大象装冰箱类似总共分三步：

第一步，初始化；通过构造函数或Init()等函数将算法类需要的参数输入进去；IntTools_FaceFace中通过SetParameters()函数设置算法的参数

第二步：计算；使用函数Build()， Perform()函数来执行计算；IntTools_FaceFace中的主要实现逻辑在Perform()中。

第三步：输出；将计算结果输出。IntTools_FaceFace通过Lines()和Points()函数输出计算结果即交线和交点。

2. Approximation Algorithm 拟合

opencascade中曲面的表示有两种方式，一种是参数方程S(u,v)表示，一种是二次曲面的代数方程f(x,y,z)=0表示。因此也将曲面求交问题分为：

• 代数/代数曲面求交；
• 代数/参数曲面求交；
• 参数/参数曲面求交；

opencascade中计算曲面求交更底层的类是IntPatch_Intersection，其中也是分这三种类型来处理：

GeomGeomPerfom()对应的是代数/代数曲面求交；

GeomParamPerform()对应的是代数/参数曲面求交；

ParamParamPerform()对应的是参数/参数曲面求交；

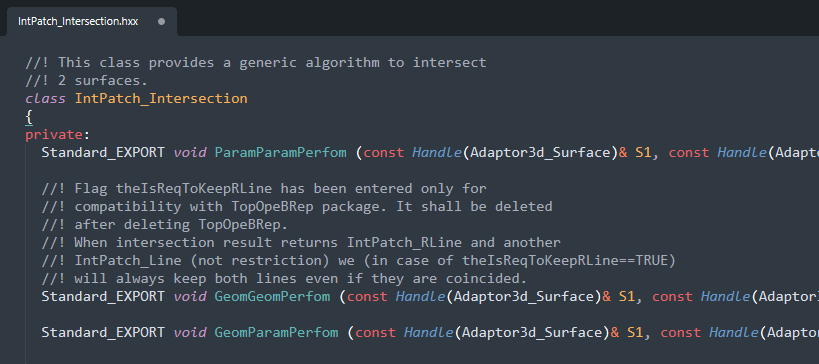
其中代数/代数曲面求交函数GeomGeomPerform()中使用类IntPatch_ImpImpIntersection来计算两个二次代数曲面的求交，其实这是Imp缩写就是隐式代数方程Implicit Equation的意思。

二次代数曲面的求交使用包IntAna来实现，这在早期文章中分析了其实现原理，主要思想是将一个二次曲面的参数表示代入隐式方程变成一元方程，然后对这个一元方程进行求解。例如圆柱面与二次代数曲面求交：

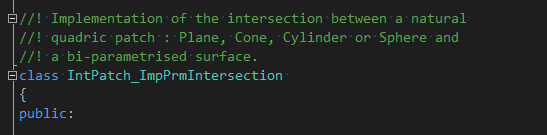
其中代数/参数曲面求交函数GeomParamPerform()中使用类IntPatch_ImpPrmIntersection来计算代数曲面和参数曲面的求交，这里Prm为Parametric equation参数方程的缩写。其代码注释中写到bi-parametrised surface意思双参数曲面S(u, v)。

其中参数/参数曲面求交函数ParamParamPerform()中使用类IntPatch_PrmPrmIntersection来计算参数数曲面和参数曲面的求交。

参数/参数曲面求交的基本方法有以下五种：

• 代数法，也称解析法；
• 网格离散法；
• 分割法；
• 迭代法；
• 追踪法；

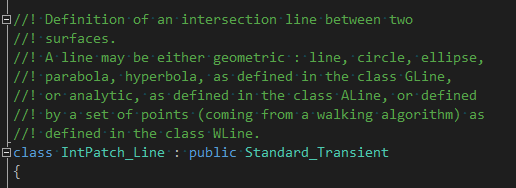
相关原理介绍可以参考朱心雄等著《自由曲线曲面造型技术》。大家可以结合源码，看看opencascade中使用了哪些方法。曲面交线的表达涉及三个问题，交点信息表示，交线组织及交线中交点的删除策略。交线的表达使用类IntPatch_Line：

在类IntTools_FaceFace中函数SetParameters()中可以指定交线中交点的删除策略。通过参数ApproxCurves和ApproximationTolerance来指定交线中交点是否拟合及拟合精度。求交过程中得到的交点往往非常致密，这样虽然可以保证交线的精度，但保存的数据量太大，在实际应用中需要删除部分交点。Pratt提出使用最小二乘法对交线逼近，以删除不必要的交点。这里就需要使用到拟合算法Approximation Algorithm。

在opencascade中拟合问题被抽象成非线性方程组的求解问题，当然最小二乘法也是其中方法之一。拟合算法是造型内核中最基础最重要的算法，除了简单的点拟合成线以外，还要处理带约束的情况，如加上交点通过曲面的位置约束等。几何约束求解器中核心也是如此。法国、俄罗斯数学厉害，我想应该是已经形成理论+应用的良性循环。数学是创新的基础，是用最简单的语言来精确描述自然中的规律，虽然我们理工科一直学数学，但工作后很大一部分人很少使用高等数学中的工具，感觉数学没什么用。学而不思则罔，思而不学则殆。我总结的学习规律就是要有实践，上学时实践就是通过做题，数学理论的一种实践就是开发出软件程序。

现在国家提倡自主我觉得是大好事，什么时候我们出一个几何内核，出一个PDE偏微方程求解器等，形成理论加实践的良性循环，以我们的人数和勤劳，离科技强国就不会太远。

3. Projection Algorithm 投影

投影主要用来计算曲面上的曲线对应到曲面参数空间的曲线PCurve，生成FACE面时如果边EDGE中没有PCurve，得到的面是不正确的。投影算法的实现原理在早期的文章中已经详细介绍过，投影算法依赖拟合算法。投影算法用在生成交线的函数中MakeCurve()：

当不对交线进行拟合时，生成交线及PCurve主要使用类GeomInt_SS的静态函数来得到交线：

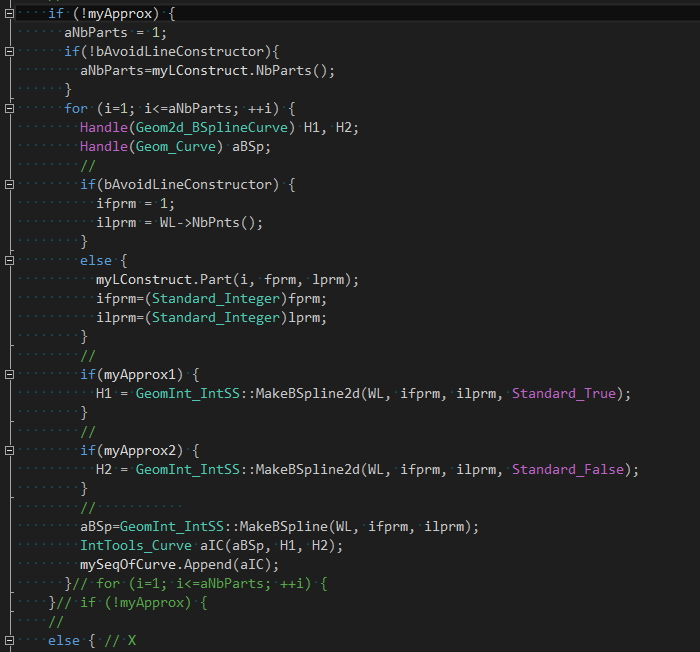
这样生成的交线是B样条曲线且控制顶点数量很大。当通过拟合可以生成更简化的B样条交线。

 

4. Classification Algorithm 定位

定位工具主要用于判断点和一个区域的状态，是在区域内、外还是上。在早期的文章中有一些介绍：https://www.cnblogs.com/opencascade/p/Point_Classifier.html

点定位在曲面求交中的应用就是处理拓朴面的情况，对于几何曲面，其实参数域就是其参数S(u,v)的取值范围。对于拓朴面，其参数域是通过边界Wire来限定的，而且还会有面上开孔的情况需要处理。其实IntTools_FaceFace主要是用来计算FACE中几何曲面求交的，没有正确处理定位问题，即生成的交线没有处理面的边界问题。相信看懂源码的同学可以解决这个问题。

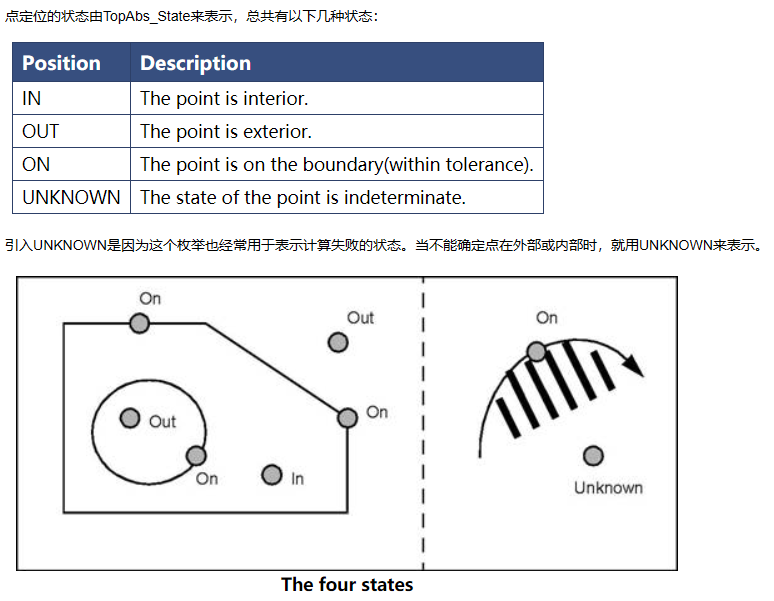
定位问题是个几何问题，在《计算几何及应用》一书中有对点的定位问题有详细算法。一般的处理方法是通过点作一条半射线，计算半射线与多边形交点的个数，若交点数为奇数，则点在内部，否则在外部。还有一种方法是通过计算点与多边形各顶点的角度来判断。这两种方式时间复杂度均为O(n)。opencascade中使用的第一种方法。书中提到几种效率更高的算法，如点定位问题的分层方法，可以将查询时间提高到O(logn)。点定位问题的单调链方法用O(nlogn)时间和O(n)空间作预处理，查询时间可以O((logn)^2)完成。点定位的三角形细分方法(Triangulation refinement method)只用O(n)空间存放预处理结果，用O(logn)时间回答点在哪个区域，完成预处理的时间是O(nlogn)。由此可见，opencascade的定位算法还有一些改进空间。

5. Conclusion

几何内核中曲面和曲面求交是最重要最复杂的问题，处理曲面和曲面求交需要拟合Approximation Algorithm、投影Projection Algorithm和定位Classification Algorithm工具。其中拟合和投影主要是数学问题，定位主要是个几何问题，理解问题就能找到相应的解决工具。庆幸有opencascade这个功能相对完备的开源的几何内核，提供了一个理论联系实践的平台。理解数学理论后可以去阅读源码，甚至是参与和贡献，求交、拟合、投影和定位工具都有一些改进空间。

最近关注的朋友说文章发得少了，主要原因是有点忙，不是因为保守不想分享，当然有些朋友也提醒要留一手。对于opencascade的技术分享我是没有保留的，因为opencascade是开源的，如果通过这些文章分享能帮助别人解决一些问题，就是创造价值，是有意义的。时不时收到网友的感谢，收获的感动不是用金钱可以衡量的。