LeetCode题解——700.二叉树搜索树中的搜索
题意:
在解决这道题之前,我们需要了解二叉搜索树(BST, Binary Search Tree)
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。二叉搜索树作为一种经典的数据结构,它既有链表的快速插入与删除操作的特点,又有数组快速查找的优势;所以应用十分广泛,例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。——源于wiki
比较通俗的来讲就是:对于一棵非空二叉树来说,满足其每一个结点的左子树中所有结点的值小于该结点的值;其右子树中所有结点的值大于该结点的值。另外对于空树和只有根节点的树我们也认为其是一棵二叉搜索树。下面是一颗二叉搜索树:
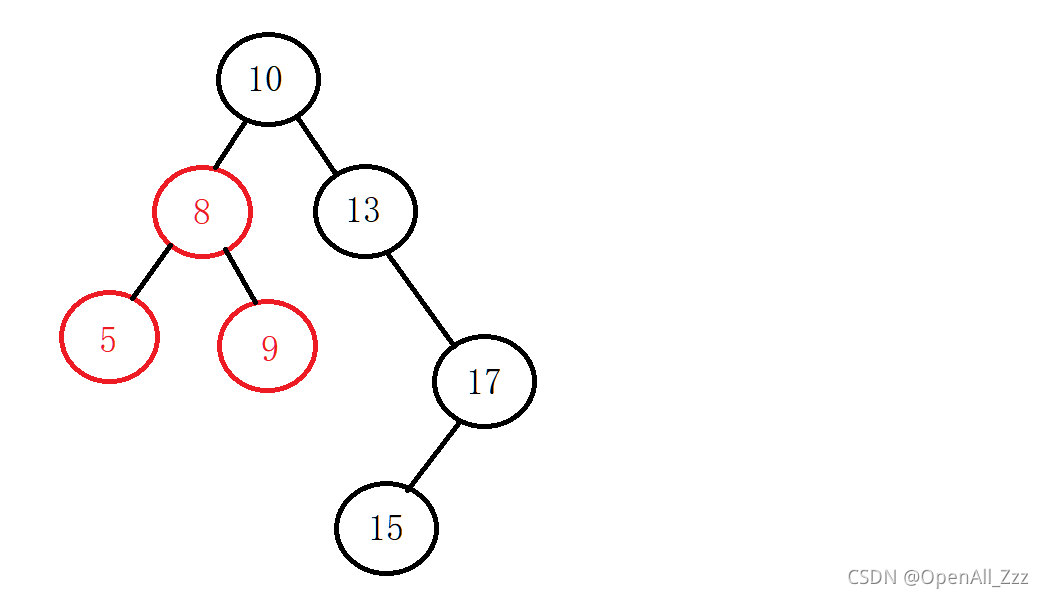
这里注意不要和堆弄混了。以大顶堆举例,堆(大顶堆)是其每个结点的值都不小于其左右孩子结点的值。
而二叉搜索树是对于其左右子树而言的。
解题思路
对于要查找的值val,我们通过比较二叉搜索树中每一个结点的值val_来得到我们下一步需要做什么,如果 val < val_ ,我们进入该结点的左子树进行查找;如果 val > val_,我们进入该结点的右子树进行查找。我们希望在这个过程中找到值为val的结点。
抽象过程
以上图的二叉搜索树举例,我们查找9,则整个过程为:
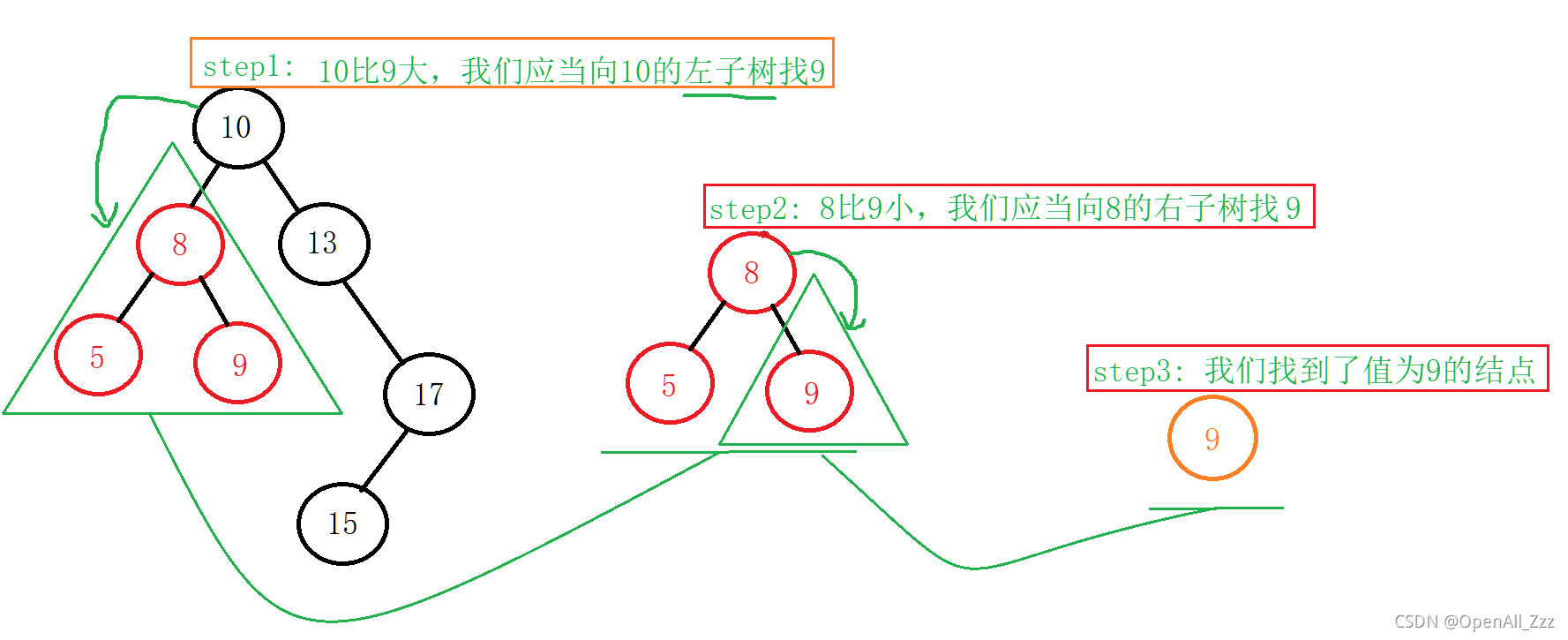
代码
struct TreeNode* searchBST(struct TreeNode* root, int val){
// 递归法
// if(root == NULL) return NULL; // 找到最后也没有找到 或者 空的二叉搜索树
// if(root->val < val) return searchBST(root->right, val); // 搜索右子树的过程
// else if(root->val > val) return searchBST(root->left, val); // 搜索左子树的过程
// return root; // 上面两种情况没有发生即找到了
// 迭代法 -- 上述递归返回的表达式不涉及递归调用,是一种尾递归,这类递归可以被写成循环迭代的形式
while(root != NULL)
{
if(root->val == val) return root; // 找到了对应的值val
if(root->val < val){
root = root->right; // 搜索右子树的过程
}
else{
root = root->left; // 搜索左子树的过程
}
}
return NULL;
}





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 终于写完轮子一部分:tcp代理 了,记录一下
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理