四千字详解分块查找
分块查找的思想
在讲解分块算法之前,我们先介绍一下有关分块查找的概念
- 概念:分块查找,也叫索引顺序查找,算法实现除了需要查找表本身之外,还需要根据查找表建立一个索引表。给定一个查找表,其对应的索引表如图所示:
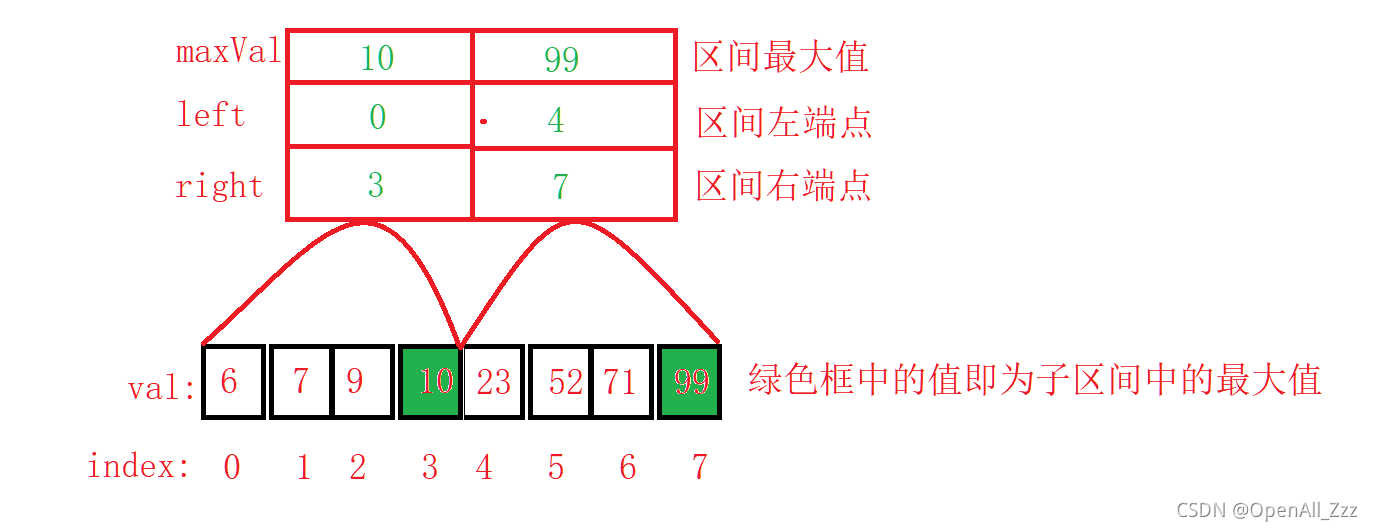
- 解释:观察上图中的 两段子区间[0, 3] 和 [4, 7] 所对应的索引表可知,对于一个索引表由①区间最大值、②区间左端点、③区间右端点,这也就是我们讲的分块查找中的块,所以索引表就概括了一个块的信息。
- 下面我们讲算法思路时,如果不做特别说明,索引表就都理解成块。
解释了相关概念,下面我们就开始讲分块查找的思路。
- 分块查找的基本思想:
- 首先将查找表分为若干子块。块内的元素可以无序也可以有序,但块之间整体是有序的(上图在数组区间[0, 3]内的元素整体都小于[4, 7]中的元素)。一般来讲,即第二个块中的所有被记录的关键字大于第一个块中的最大关键字,第三个块中的所有被记录的关键字大于第二个块中最大的关键字,… ,以此类推。这种有序就是分块有序。
- 对于我们要查找的值val,我们分两个步骤:①针对子块有序,我们采用折半查找(也可以顺序查找),我们先确定val应该在哪个子块中(也可能会找不到),②针对所找到的子块,我们采用只能直接采用顺序查找(因为在实际应用上它基本上是无序的,对于基本有序也是无序,也只能采用顺序查找)。
现在我们来引入一个相关的案例

- 这是笔者的学校有关数据结构课程的一道实验题。
- 对于这道题,很显然是一道分块查找的算法设计题。我们首先先创建了一个数据量为1000的数据表,然后分为四部分的创建,例如第一部分,在[0, 249]的区间中随机存放了1到250中每一个的数,这就说明,在该部分每个数都是唯一的,其他三部分也是同样的方法创建的,最终,整体的数据表的数据范围就是[1, 1000],且每个数都唯一。
- 接着,对于每个块我们进行折半查找,找出val所在的块;针对找到的块进行顺序查找,找出val。
针对每个块的折半查找,它不同于对普通的整型进行的折半查找,我们需要进一步探索。
-
问:针对块[2, 4, 6, 7] (每个数字代表的是每个块中的最大关键字)我们如何分别对数0、3、9所确定其所属的块呢?分别来看。
-
对于0:

-
对于3:

-
对于9:

-
只有分析出上述三种情况,才能在面对分块查找时有十足的把握!
-
建议大家独自分析上述的三种情况
C代码 —— 可在VS2019中运行
#define _CRT_SECURE_NO_WARNINGS 1
#define pages 1000
/*
* 创建一本书的页数的索引表 [1, 1000]
*/
#include <stdio.h>
#include <assert.h>
// 索引表
typedef struct
{
int maxValue; // 所选块中的最大关键字
int left; // 块所在的区间的左端点
int right; // 块所在的区间的右端点
}IndexTable;
// 只是为了测试分块查找。一般索引表不需要自己写
IndexTable* InitIndexTable()
{
// 开辟大小为4的索引表的数组空间
IndexTable* res = (IndexTable*)malloc(sizeof(IndexTable) * 4);
// 建立索引信息,默认索引表按关键字是严格升序的
for (int i = 0; i < 4; i++) {
res[i].maxValue = 250 * (i + 1);
res[i].left = i * 250;
res[i].right = 250 * (i + 1) - 1;
}
return res;
}
int BlockingSearch(int* nums, IndexTable* table, int tableSize, int targetVal)
{
// 1. 先查找块
int begin = 0, end = tableSize - 1;
int mid = (begin + end) / 2;
int targetBlock = 0;
// 对于二分法找块,边界情况分两种,需要特判
// 1. begie越界;2. end越界。
while (begin <= end)
{
if (table[mid].maxValue < targetVal)
{
begin = mid + 1;
}
else if (table[mid].maxValue > targetVal)
{
end = mid - 1;
}
else
{
targetBlock = mid;
break;
}
mid = (begin + end) / 2;
}
//
if (begin > end)
{
// 一般情况,我们必然是在begin块中查找目标值
targetBlock = begin;
// begin越界
// targetVal超过了索引表中所有的关键值,这是必然找不到的。
if (begin > tableSize - 1) return -1;
// end越界
// tagetgetVal虽然小于所有的关键值,但是不能确保必然找不到,因为关键值存的是每个子区间的最大值。
if (end < 0) targetBlock = begin;
}
// 2. 由于块内的元素是无序的,我们在块内进行顺序查找
for (int i = table[targetBlock].left; i < table[targetBlock].right; i++)
{
if (nums[i] == targetVal) return i;
}
return -1;
}
int main()
{
int index[pages];
int val = 0;
FILE* pF = NULL;
assert(pF = fopen("pagesRandom.txt", "r"));
for (int i = 0; i < pages; i++) assert(fscanf(pF, "%d", &index[i]));
IndexTable* table = InitIndexTable();
printf("请输入你需要查找的关键字的值:");
assert(scanf("%d", &val));
int res = BlockingSearch(index, table, 4, val);
// if(res) 这段语句不能这么写,在C语言中0为假,非0为真,所以对于负数来说,其也为真
if (res >= 0)
{
printf("%d在原数据中的索引是:%d\n", val, res);
}
else
{
printf("原数组中无目标值%d\n", val);
}
return 0;
}
测试数据地址:pagesRandom.txt





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)