【备战蓝桥杯国赛-国赛真题】最大数字
题目链接:https://www.dotcpp.com/oj/problem2694.html
思路
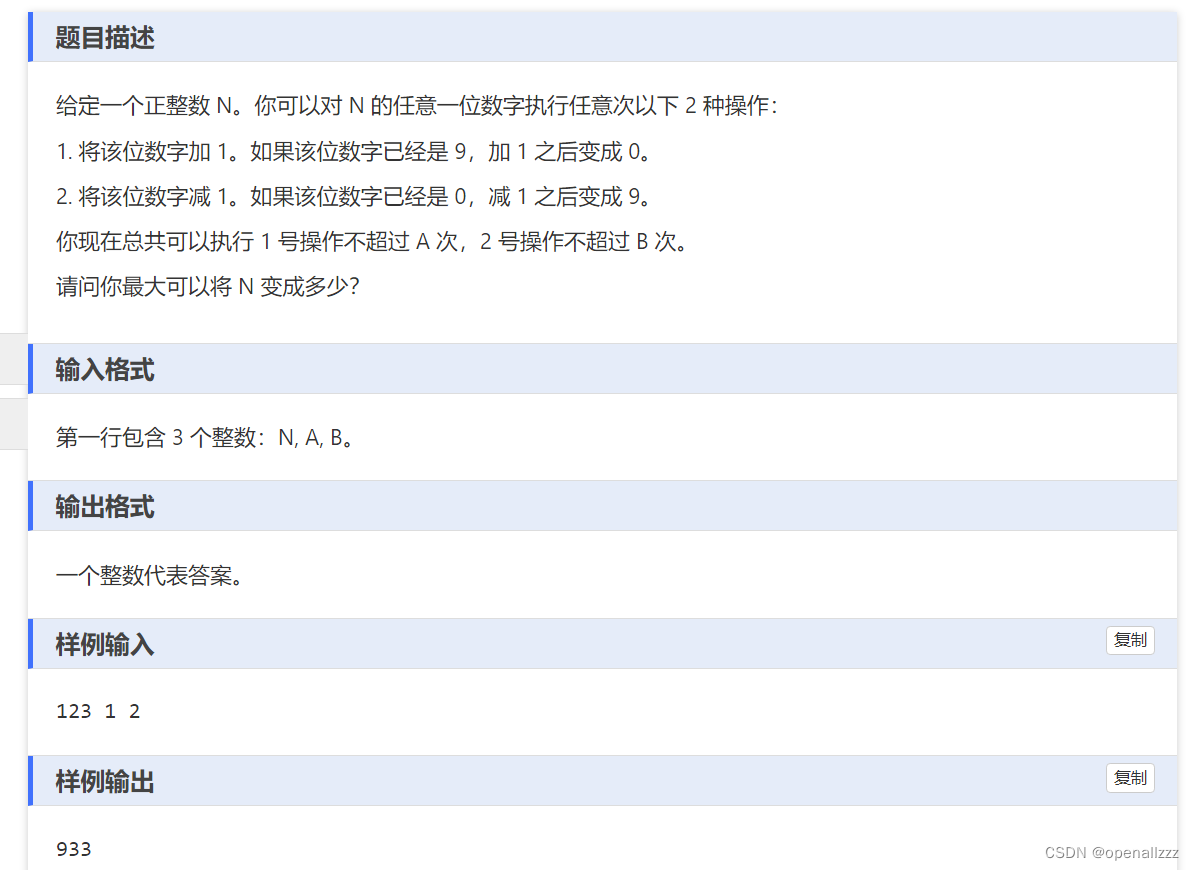
我们的目标通过若干次的两类操作(有次数限制),使得最终的数字尽可能大,而数字的大小与数的位数有关,并且处于高位的数字需要尽可能的高。本题的数据范围是1e17,看起来很大,但是分析之后我们只需要考虑其中的每一位,也只有20不到的数据量,接着我们来分析这两类操作(从高位到低位考虑):
- 加1操作:应该尽可能将数字增加到9,如果已经是9,那么我们贪心考虑的结果是,不需要对当前位进行操作,如果该操作的次数不足以让数字增加到9,那么我们全部操作完即可。
- 减1操作:该操作的目的其实只有一个,就是把该位的数字减到9,因为如果减少不到9,那么数的值将会变小,如果减少到8,那说明一定可以减少到9,并且减少到8或者更小都不如减少到9更优,因此,如果该位减少不到9,那么我们不对该位进行减1操作。
- 说明:可以证明,在最优方案中,这两种操作不会对同一位进行大于0次的操作,为了方便,我们称之为合操作。一个直观的解释是这样的,这两种的操作是互相抵消的,如果合操作存在,那么另任意一种操作数为0后,结果一定也能达到,并且增加了另一种操作的可操作次数,这样不会使得最终结果更糟糕。
接下来就是代码部分了,使用爆搜就可以,2^17的复杂度很友好,如果对下面中的代码有不理解的地方,欢迎大家交流。
代码(C++)
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
LL n, res = 0;
int a, b;
string s;
void dfs(int u, LL v) {
if(u == (int)s.size()) {
res = max(res, v);
return ;
}
LL x = s[u] - '0';
LL t = min((LL)a, 9 - x);
a -= t;
dfs(u + 1, v * 10ll + x + t);
a += t;
if(b >= x + 1) {
b -= x + 1;
dfs(u + 1, v * 10ll + 9ll);
b += x + 1;
}
}
int main() {
cin >> n >> a >> b;
s = to_string(n);
dfs(0, 0ll);
cout << res << "\n";
return 0;
}





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 终于写完轮子一部分:tcp代理 了,记录一下
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理