【备战蓝桥杯国赛-国赛真题】游园安排

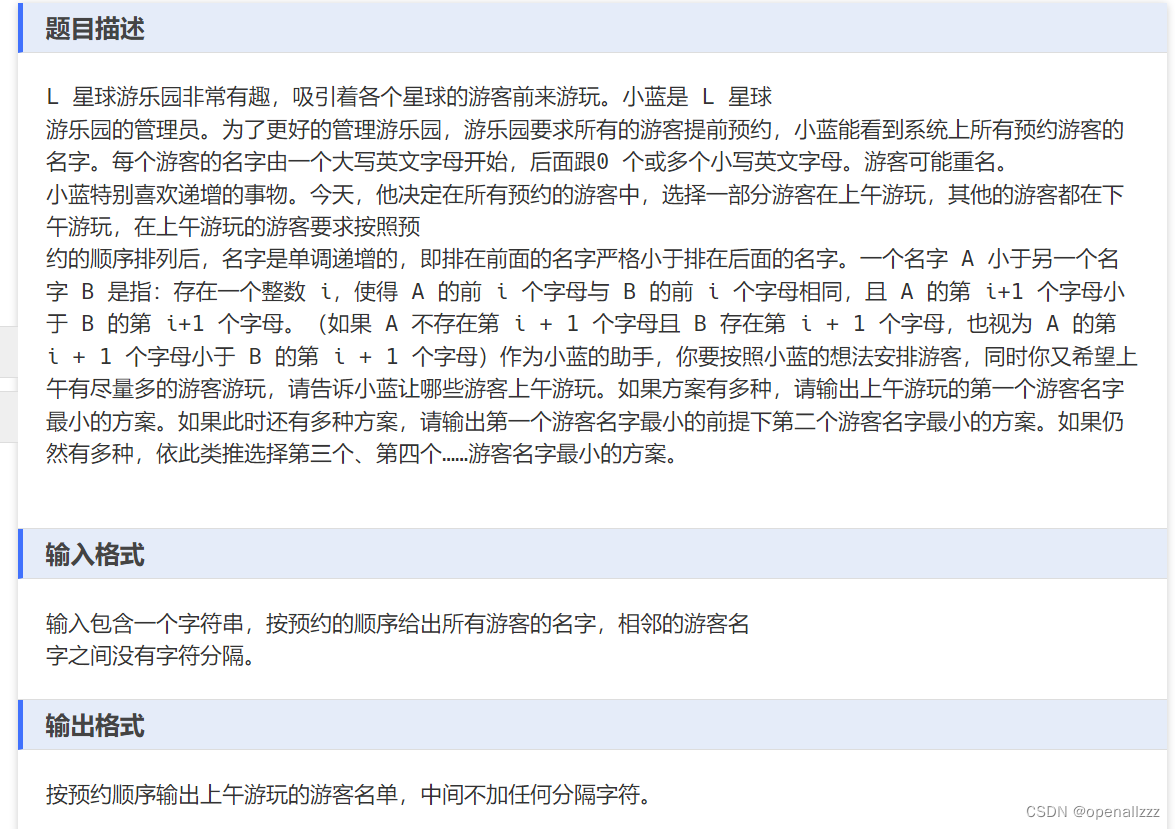
题目

http://lx.lanqiao.cn/problem.page?gpid=T2874

思路

找出一个子序列，并且是严格从小到大的子序列，结果需要尽可能的大，其实就是最长上升子序列的另外一种说法，读到这里题目就可以开始分析了。

从数据范围可以知道，最多有1e6个单词，用普通的n^2写法只能拿到70%的分数，显然，要拿到全部的分数，需要用二分优化的写法，并且该题需要输出方案，一般的dp问题输出方案，都是倒序从最终态往最初态逆推，但是该题的二分写法不需要用到状态数组，我们需要一个记录状态的数组record，其中record[i]表示当前位置i是长度为r + 1的上升子序列的最后一个字符串的下标（从0开始），然后我们从最长的LIS长度开始往前逆推即可。

C++代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 1000010;

string s;
int record[N], n;
string p[N];
string strs[N];

int main() {
    cin >> s; s += 'A';
    for(int i = 0, prev = -1; i < s.size(); i ++) {
        char c = s[i];
        if(c >= 'A' && c <= 'Z') {
            if(prev != -1) strs[n ++ ] = s.substr(prev, i - prev);
            prev = i;
        }
    }

    int len = 0;
    for(int i = 0; i < n; i ++) {
        string t = strs[i];
        int l = 0, r = len;
        while(l < r) {
            int mid = l + r + 1 >> 1;
            if(p[mid] < t) l = mid;
            else r = mid - 1;
        }

        if(p[r] >= t) continue;

        p[r + 1] = t;
        len = max(len, r + 1);
        record[i] = r + 1; // 当前位置i是长度为r + 1的上升子序列的最后一个字符串的下标
    }

    vector<string> res;
    for(int i = n - 1; i >= 0; i --) {
        if(len <= 0) break;
        if(record[i] == len) {
            res.push_back(strs[i]);
            len -- ;
        }
    }

    for(int i = res.size() - 1; i >= 0; i --) cout << res[i];
    return 0;
}