自我学习与理解:keras框架下的深度学习(一)手写体数字识别
这个系列文章主要记录使用keras框架来搭建深度学习模型的学习过程,其中有一些自己的想法和体会,主要学习的书籍是:Deep Learning with Python,使用的IDE是pycharm,需要安装keras和tensorflow库。
本文第一部分编写一个简单的深度学习网络来识别手写数字。难度不是很大,主要是对keras框架中语句的调用,以及参数的改写(keras已经把深度学习中的一系列操作打包成了函数或者编程文件,所以我们只需要调用即可)。该深度学习模型的主要步骤是:首先对数据进行预处理,变成归一化的浮点型数值矩阵输入神经网络的输入层,然后第一层的权重与输入的数据做运算后加上权重b,通过一个非线性函数输入到下一层,其他层类似;最后在输出层设有10个神经元,表示最后的输出是一个一行十列的数组,用来存放估计的数字的概率。之后由损失函数(categorical_crossentropy)进行后向传播来更新网络中的权重,其中所用到的优化器是rmsprop。
第二部分是编写一个简单梯度下降算法,类似于自己编写简单的梯度下降算法,只要清楚的了解深度学习的每个步骤,就可以自己尝试编写代码完成,从简单的开始,一步步去优化。这样会更加有利于去理解keras中的每个步骤是怎么来的,对深度学习的每个步骤理解更深。在之后的文章中,可能会慢慢的把深度学习中的步骤一一的尝试去实现。
在深度学习中的深度指的是数据模型中包含着的多个层次,而深度学习是对一堆数值做数学运算,但是这种数学运算是高纬度的,是大量的;在这些数学运算中,深度学习中的层通过反馈(比如后向传播)来对参数进行调整,然后再进行计算。如此反复数次,从而越来越接近我们所给出的正确结果。而在这个过程中,深度学习中的每个层所学习到的就是参数的具体数值。模型训练好以后,只需要一个输入,就能得到相应的输出。
对于深度学习的编程,以下是具体步骤(针对于keras框架):
1.对数据的预处理,如把图片数据变成数值矩阵,把离散的数据变成向量,把数据归一化等等,其目的是为了之后的学习;2.搭建网络框架,即输入层,隐藏层和输出层,深度学习所需要学习的参数在这些层里面;3.编译,即定义所需要用的优化器、损失函数等;4.循环训练,让网络一次又一次的运行,最后得到学习后的参数;5.测试训练的网络模型,在模型训练结束后,进行测试来验证其泛化能力。
手写体识别:
我们使用mnist数据集,这个数据集包含60000张训练图像和10000张测试图像,全部都是尺寸28*28像素的手写数字图片,如下图所示:

以下我们使用keras框架进行手写体识别的程序编写:
1.对数据的预处理
from keras.datasets import mnist (train_image,train_labels),(test_images,test_labels)=mnist.load_data()
第一句是从keras.datasets中导入mnist,具体来说,我们在pychram中下载了keras这个库。它是一个文件夹,里面由很多的文件,而其中一个文件是datasets,里面主要用来调用各种数据集;比如mnist是keras文件下datasets文件中的一个编程文件(.py),和我们自己写的编程文件没有区别,而这个文件的具体功能是取爬取到mnist网站中的训练集和测试集。在mnist中有一个load_data的函数,在该函数中把训练集和测试集都分类好了,所以我们用(train_image,train_labels),(test_images,test_labels)来调用该函数中的训练集和测试集。训练集是为了训练模型识别手写体,而测试集是为了检测模型训练好之后对其他非训练集图片识别的能力,也就是泛化能力,而模型的优秀泛化能力是我们所需要的。
其中train_image的类型是一个三维张量:(60000,28,28),即是拥有60000张28*28的照片。而train_labels是一个一维的张量:(60000,),表示有60000个标签。测试集test也和训练集合类似,只是照片总数只有10000张,所以标签也只有10000个。
在导入数据集后,我们首先对数据进行处理,首先我们得确定深度学习网络是用什么层来搭建,我们假设使用全连接层(后面会讲到用卷积网络),则需要把图片数据处理成一个矩阵输入,该矩阵的多少行表示是有多少张照片,列是图像28*28个像素值(把图片拉成一维的)因为矩阵内是灰色图片的像素点,又需要把矩阵里面的数值压缩到0到1之间变成float32类型,所以我们需要把矩阵内的数值变成浮点型变量后除以255,最后还需要对标签(是什么数字)处理成为一个一维的向量(one-hot),比如,如果标签是3(对应的图片是手写体数字3),则生成一个只在索引3写入1,其他地方写入0的一维向量:[0,0,0,1,0,0,0,0,0,0,]。代码如下:
train_image=train_image.reshape((60000,28*28)) #定义训练集的数据类型,是一个(60000,784)的矩阵 train_image=train_image.astype('float32')/255 #把以上定义的矩阵内数值变成一个在(0,1)之间的数 test_images=test_images.reshape((10000,28*28)) #同上 test_images=test_images.astype('float32')/255 train_labels = to_categorical(train_labels) test_labels = to_categorical(test_labels)
2.搭建网络框架
from keras import models from keras import layers network=models.Sequential() network.add(layers.Dense(512,activation='relu',input_shape=(28*28,))) network.add(layers.Dense(10,activation='softmax'))
首先需要导入models和layers,即导入keras中编写好了的层和模型,第一行和第二行是要放在最前面的(所有的导入都需要放在最前面,这里为了方便讲解,所以和相应的代码放在一起)
我们可以想象该程序在keras这个文件中,导入models编程文件和layers文件,然后使得network为models.Sequential(),sequential是models中的一个函数,表示以下的网络结构都是线性排列下去。
然后我们添加了两个全连接层(Dense),该网络一共就只有两个层次。第一层,神经元是512个,激活函数是relu函数,而且定义了输入的形状,其参数一共有:28*28*512+512=401920(图像像素尺寸*神经元个数+权值b)。第二层是最后一层也是输出层,因为是判断手写数字,所以是10个神经元,表示输出10个概率值(总和为1)的列表,其中激活函数是softmax,其参数一共有:512*10+10=5120(上一层神经元个数*该层神经元个数+权值b)。
3.编译
network.compile( optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'] )
这一步是为第二步定义的网络结构做训练的准备,其中有三个参数:1.损失函数(loss):告诉网络学习的情况,如何让网络朝着争取的放向进行。(告诉网络,你和正确值差了多少,然后用优化器来反馈信号(后向传播)进行参数更新)2.优化器(optimizer):用于训练数据和损失函数来更新网络的机制。3训练过程中需要监视的指标(metrics):这里只监视训练的正确率如何(把每一次运行的accuracy的数值打印在页面)
4.循环训练
network.fit(train_image,train_labels,epochs=100,batch_size=34)
用之前定义的network调用fit函数执行循环训练,在fit中,train_image和train_labels是训练要使用的图片数据和标签,epochs是指训练多少次,batch_size是指一次训练多少个数据(比如每一次epoch中,一共要训练60000组数据,但是一次性只训练34次)。在这里的代码,我们可以令其等于一个变量,然后在最后画出准确率和损失值的图形(详细方法在下篇文章讨论)
5.测试训练的网络模型
test=network.evaluate(test_images,test_labels) print(test)
在network中调用evaluate函数对最后的测试集进行评估,然后把数赋值给test,最后把test打印出来,得到最后的acc(准确度)和loss(损失值)。一般来说,最后的测试是在训练好了模型之后,去测试模型的泛化能力。
总代码如下:
from keras.datasets import mnist from keras import models from keras import layers from keras.utils import to_categorical #导入数据集 (train_image,train_labels),(test_images,test_labels) = mnist.load_data() #数据预处理 train_image=train_image.reshape((60000,28*28)) #定义训练集的数据类型,是一个(60000,784)的矩阵 train_image=train_image.astype('float32')/255 #把以上定义的矩阵内数值,归一化 test_images=test_images.reshape((10000,28*28)) #同上 test_images=test_images.astype('float32')/255 train_labels = to_categorical(train_labels) test_labels = to_categorical(test_labels) #定义网络架构 network=models.Sequential() network.add(layers.Dense(512,activation='relu',input_shape=(28*28,))) network.add(layers.Dense(10,activation='softmax')) #编译 network.compile( optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'] ) #开始循环训练网络 network.fit(train_image,train_labels,epochs=100,batch_size=34) #对网络进行评估 test=network.evaluate(test_images,test_labels) print(test)
以上是编写一个简单的深度学习网络来识别手写数字。难度不是很大,主要是对keras框架中语句的调用,以及参数的改写(keras已经把深度学习中的一系列操作打包成了函数或者编程文件,所以我们只需要调用即可)。该深度学习模型的主要步骤是:首先对数据进行预处理,变成归一化的浮点型数值矩阵输入神经网络的输入层,然后第一层的权重与输入的数据做运算后加上权重b,通过一个非线性函数输入到下一层,其他层类似;最后在输出层设有10个神经元,表示最后的输出是一个一行十列的数组,用来存放估计的数字的概率。之后由损失函数(categorical_crossentropy)进行后向传播来更新网络中的权重,其中所用到的优化器是rmsprop。
附:梯度下降算法
梯度下降算法其内容不是很难,主要是在某个点找到其梯度的方向,然后选择梯度的反方向移动,最后慢慢的接近函数的极值点。
举个简单的例子,令f(x)=x**2(函数是x的平方),然后取一个点:x=2,下面我们编写其梯度下降的算法。
在编写之前,我们首先要明白,梯度下降算法是怎么慢慢的接近极值点的。在上面例子中,我们选定点x=2后,我们在x=2这一点求其导数,然后用x减去该导数乘以学习率,得到一个新的x坐标,计算出函数的值,再重复以上步骤,让其慢慢接近极值点(导数为零,或者每一次移动都足够小,小到满足需求)。
其python程序如下:
首先我们定义f(x)函数,以及其一阶导函数fn(x):
def f(x): f=x**2 return f def fn(x): h=0.0001 fn=(f(x+h)-f(x-h))/(2*h) return fn
注:fn=(f(x+h)-f(x-h))/(2*h)是取了x两边的变化(中心差分),这会使得导数误差更小。
然后定义学习率,循环的次数以及x的初始值,代码如下:
eta=0.01 #学习率 mun_times=1000 #循环次数 x_value=[] #保存x的值 f_value=[] #保存f(x)的值 x=2 #让x从2开始取值
之后就是通过循环,不断的接近函数的极值:
for i in range(mun_times): x-=eta*fn(x) #更新x的取值 x_value.append(x) f_value.append(f(x))
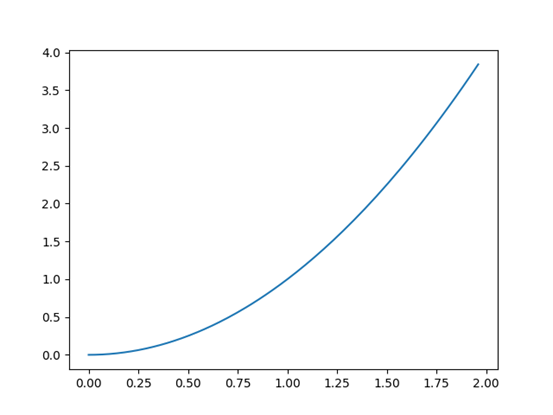
最后可以把x的每次取值和f(x)的值画出来,看看梯度下降的轨迹图:
import matplotlib.pyplot as plt plt.plot(x_value,f_value) plt.show()
图形如下图所示:
总的代码为:
import matplotlib.pyplot as plt def f(x): f=x**2 return f def fn(x): #输入的是x输出的是derivate h=0.0001 fn=(f(x+h)-f(x-h))/(2*h) return fn eta=0.01 #学习率 mun_times=1000 #循环次数 x_value=[] #保存x的值 f_value=[] #保存f(x)的值 x=2 #让x从2开始取值 for i in range(mun_times): x-=eta*fn(x) #更新x的取值 x_value.append(x) f_value.append(f(x)) plt.plot(x_value,f_value) plt.show()
下面讨论一下偏导数的梯度下降,核心思想是求出x(x在这里是一个列表,有多个数值)的偏导数,然后把梯度存储在一个列表中,最后总的进行数值更新:
首先我们定义其求偏导的过程,即分别求x列表中的每个x的偏导数:
def gradient(f,x): h=0.0001 grad = np.zeros_like(x) #生成一个与x大小一致的全零矩阵 for i in range(x.size): tem = x[i] x[i] = tem + h #求第i个x的前向差分 fh1 = f(x) x[i] = tem - h #求第i个x的后向差分 fh2 = f(x) grad[i] = (fh1-fh2)/(2*h) #求第i个x的中心差分 x[i] = tem #把第i个x的值还给它自己 return grad
定义函数,这里为了方便,我们只定义一个包含两个变量的函数:
def function(x): return x[0]**2+x[1]**2
定义初始参数:
x_list1=[] #存储x[0]的值 x_list2=[] #存储x[1]的值 function_list=[] #存储函数的值 x = np.array([-2.0,4.0]) #选定初始的点 lr=0.01 #学习率是0.01 ste_num=500 #循环500次
梯度下降:
for i in range(ste_num): x_list1.append(x[0]) x_list2.append(x[1]) function_list.append(function(x)) grad=gradient(function,x) #计算x的梯度 x -= lr * grad #更新x的值
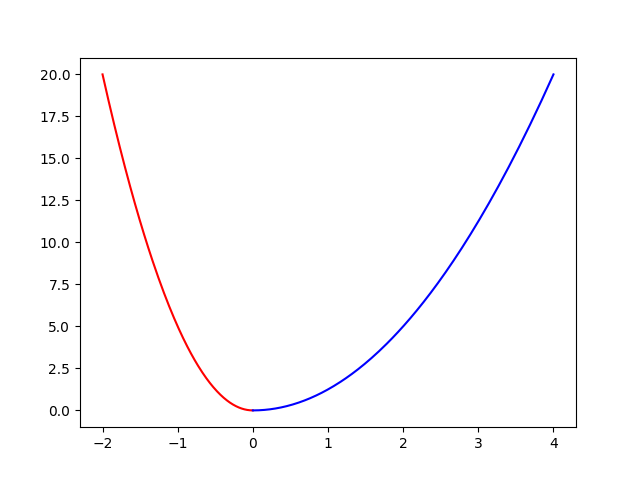
最后画图查看:
import matplotlib.pyplot as plt plt.plot(x_list1,function_list,'r',label='x[0]') plt.plot(x_list2,function_list,'b',label='x[1]') plt.show()
总代码:
import numpy as np import matplotlib.pyplot as plt def gradient(f,x): h=0.0001 grad = np.zeros_like(x) for i in range(x.size): tem = x[i] x[i] = tem + h fh1 = f(x) x[i] = tem - h fh2 = f(x) grad[i] = (fh1-fh2)/(2*h) x[i] = tem return grad def function(x): return x[0]**2+x[1]**2 x_list1=[] #存储x[0]的值 x_list2=[] #存储x[1]的值 function_list=[] #存储函数的值 x = np.array([-2.0,4.0]) #选定初始的点 lr=0.01 #学习率是0.01 ste_num=500 #循环500次 for i in range(ste_num): x_list1.append(x[0]) x_list2.append(x[1]) function_list.append(function(x)) grad=gradient(function,x) #计算x的梯度 x -= lr * grad #更新x的值 plt.plot(x_list1,function_list,'r',label='x[0]') plt.plot(x_list2,function_list,'b',label='x[1]') plt.show()
深度学习的梯度下降类似于以上的过程,不过要比上面的例子复杂很多。
类似于自己编写的简单梯度下降算法,只要清楚的了解深度学习的每个步骤,就可以自己尝试编写代码完成,从简单的开始,一步步去优化。这样会更加有利于去理解keras中的每个步骤是怎么来的,对深度学习的每个步骤理解更深。在之后的文章中,可能会慢慢的把深度学习中的步骤一一的尝试去实现。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号