条件随机场入门(二) 条件随机场的模型表示
linear-chain 条件随机场
条件随机场(conditional random field)是给定随机变量 X 条件下,随机变量 Y 的马尔可夫随机场。本文主要介绍定义在线性链上的特殊的条件随机场,称为线性链条件随机场(linear-chain CRF)。线性链条件随机场可以用于机器学习里的标注问题。这时,在条件概率模型 $P(Y|X)$ 中,Y 是输出变量,表示标记序列,也把标记序列称为状态序列(同 HMM 中的状态序列);X 是输入变量,表示观测序。学习时,利用训练数据集通过极大似然估计或正则化的极大似然估计得到条件概率模型 $\hat{P}(Y|X)$ ;然后使用该模型预测即可。
CRF 的定义
设 X 与 Y 是随机变量,$P(Y|X)$ 是在给定 X 的条件下 Y 的条件概率分布。若随机变量 Y 构成一个由无向图 G = (V,E) 表示的马尔可夫随机场,即:
\[P(Y_v|X,Y_w,w \ne v) =P(Y_v|X,Y_w,w \sim v) \]
对任意结点 v 成立,则称条件概率分布 $P(Y|X)$ 为条件随机场。式中 $w \sim v$ 表示在图 G = (V,E) 中与结点 v 有边连接的所有结点 w, $w \ne v$ 表示结点 v 以外的所有结点,$Y_u,Y_v,Y_w$ 为结点 $u,v,w$ 对应的随机变量,从定义来看,左边到右边点的数量大大减小,$w \ne v$ 的点有 $|V|-1$ 个,而 $w \sim v$ 就少了,其实就是说当前变量只跟与之相邻的变量有关系,而独立于没有直接连接的变量。
在定义中并没有要求 X 和 Y 具有相同的结构。现实中,一般假设 X 和 Y 有相同的图结构。本书主要考虑无向图为线性链的情况,即对于节点 1 到 n,边的情为: $E = \left \{ (i,i+1) \right \}_{i=1}^{n-1}$ ,在此情况下 $X =\left \{ X_i \right \}_{i=1}^{n} ,Y =\left \{ Y_i \right \}_{i=1}^{n}$ ,最大团是相邻两个结点的集合,下图即为 liner-chain CRF:
 线性链条件随机场的定义:设 $X =\left \{ X_i \right \}_{i=1}^{n} , \ Y =\left \{ Y_i \right \}_{i=1}^{n}$ 均为线性链表示的随机变量序列,若在给定随机变量序列 X 的条件下,随机变量序列 Y 的条件概率分布 P(Y|X)构成条件随机场,即满足马尔可夫性
线性链条件随机场的定义:设 $X =\left \{ X_i \right \}_{i=1}^{n} , \ Y =\left \{ Y_i \right \}_{i=1}^{n}$ 均为线性链表示的随机变量序列,若在给定随机变量序列 X 的条件下,随机变量序列 Y 的条件概率分布 P(Y|X)构成条件随机场,即满足马尔可夫性
\[P(Y_i | X,Y_1,…,Y_{i-1},Y_{i+1},…,Y_n) = P(Y_i | X,Y_{i-1},Y_{i+1})\]
则称 $P(Y|X)$ 为线性链条件随机场。注意当 $i = 1$ 或 $i = n$ 时只考虑一侧,在标注问题中,X 表示输入观测序列,Y 表示对应的输出标记序列或状态序列。
CRF 的参数化形式
根据 Hammersley-Clifford 定理,可以给出线性链条件随机场 $P(Y|X)$的因子分解式,各因子是定义在相邻两个结点上的函数。在随机变量 X 取值为 x 的条件下,随机变量 Y 取值为 y 的条件概率具有如下形式:
\[P(y|x) = \frac{1}{Z(x)}\exp \left \{ \sum_{i,k}\lambda_k t_k (y_{i-1},y_i,x,i)+ \sum_{i,l}\mu_l s_l(y_i,x,i) \right \}\]
其中 Z(x) 为归一化项:
\[Z(x) = \sum_y \left \{ \sum_{i,k}\lambda_k t_k (y_{i-1},y_i,x,i)+ \sum_{i,l}\mu_l s_l(y_i,x,i) \right \}\]
式中, $t_k$ 和 $s_l$ 是特征函数,$\lambda_k$ 和 $\mu_l$ 是对应的权值。 $Z(x)$ 是规范化因子,求和是在所有可能的输出序列上进行的。以上两个式子是线性链条件随机场模型的基本形式,表示给定输入序列 x ,对输出序列 y 预测的条件概率。其中 $t_k$ 是定义在边上的特征函数,称为转移特征( t 是transition的缩写),依赖于当前和前一个位置, $s_l$ 是定义在结点上的特征函数,称为状态特征(s 是status的缩写),依赖于当前位置(无论哪种特征函数,都将当前可能的 $y_i$ 作为数)。 $t_k$ 和 $s_l$ 都依赖于位置,是局部特征函数。通常,特征函数 $t_k$ 和 $s_l$ 取值为 1 或 0 ;当满足特征条件时取值为 1 ,否则为 0 。CRF 完全由特征函数和对应的权值 $\lambda_k,\mu_l$ 确定,线性链条件随机场也是对数线性模型(loglinear model)。
CRF 的简化形式
CRF 还可以由简化形式表示。注意到条件随机场式中同一特征在各个位置都有定义,可以对同一个特征在各个位置求和,将局部特征函数转化为一个全局特征函数,这样就可以将条件随机场写成权值向量和特征向量的内积形式,即条件随机场的简化形式,为简便起见,首先将转移特征和状态特征及其权值用统一的符号表示。设有 $K_1$ 个转移特征,$K_2$ 个状态特征,记
\[f_k(y_{i-1},y_i,x,i) = \left \{ \begin{aligned}
&t_k(y_{i-1},y_i,x,i), \ \ k = 1,2,...,K_1 \\
&s_t(y_i,x,i), \ \ \ \ \ \ \ \ \ \ k = K_1 + l ; l = 1,2,...,K_2
\end{aligned}\right.\]
上式其实是对特征函数进行编码,编号的前 $K_1$ 个属于转移特征,后 $K_2$ 个属于状态特征。记 $K = K_1 + K_2$ ,编号统一了,后面就可以放到同一个矩阵里了。
然后,对转移与状态特征在各个位置 i 求和,记作
\[f_k(y,x) = \sum_{i=1}^nf_k(y_{i-1},y_i,x,i), \ \ \ k = 1,2,…,K\]
上式的特征函数虽然都写成接受 4 个参数的形式,但对状态特征函数而言,$y_{i-1}$ 是会被忽略掉的,用 $w_k$ 表示特征$f_k(y,x)$ 的权值,即:
\[w_k = \left \{ \begin{aligned}
&\lambda_k, \ \ k = 1,2,...,K_1 \\
&\mu_l, \ \ k = K_1 + l ; l = 1,2,...,K_2
\end{aligned}\right.\]
于是,条件随机场可表示为:
\begin{aligned}
P(y|x) &= \frac{1}{Z(x)} \exp \left \{ \sum_{k=1}^K w_k f_k(y,x) \right \}\\
Z(x) &= \sum_y \exp \left \{ \sum_{k=1}^Kw_kf_k(y,x)\right \}
\end{aligned}
若 w 表示权值向量,即
\[w= (w_1,w_2,…,w_K)^T\]
以 F(y,x) 表示全局特征向量,即:
\[F(y,x) = \left \{ f_1(y,x), f_2(y,x),…,f_K(y,x) \right \}^T\]
则条件随机场可以写成向量 w 与 F(y,x) 的内积的形式:
\[P_w(y|x) = \frac{\exp\left \{w \cdot F(y,x)\right \} }{Z_w(x)}\]
其中,
\[Z_w(x) = \sum_y \exp \left \{ w \cdot F(y,x) \right \}\]
条件随机场的矩阵形式
条件随机场还可以由矩阵表示。假设 $P_w(y|x)$ 是由内积形式给出的线性链条件随机场,表示对给定观测序列 x ,相应的标记序列 y 的条件概率。引进特殊的起点和终点状态标记 $y_0 = start , y_{n+1} = stop$,这时 $P_w(y|x)$ 可以通过矩阵形式表示。
对观测序列 x 的每一个位置 $i=1,2,…,n+1$,定义一个 m 阶矩阵(m 是标记 $y_i$ 取值的个数,因为 x 是给定的,$ i-1 和位置 i 各有 m 种可能,所以是 m 阶矩阵):
\begin{aligned}
M_i(x) &= \left \{ M_i(y_{i-1},y_i|x)\right \} \\
M_i(y_{i-1},y_i|x)&= \exp \left \{ W_i(y_{i-1} ,y_i|x)\right \}\\
M_i(y_{i-1},y_i|x)&= \sum_{k=1}^Kw_k \cdot f_k(y_{i-1},y_i,x,i)
\end{aligned}
其实矩阵定义了一个 状态 $y_{i-1}$ 的 m 种状态到 $y_i$ 的 m 种状态的转移的概率:
\begin{aligned}
M_i(y_{i-1} ,y_i|x) &= \exp\left\{ \sum_k\lambda_kf_k(y_{i-1},y_i,x,i)\right\} \\
&=\exp\left\{ \sum_k\lambda_kt_k(y_{i-1},y_i,x,i) + \sum_l\mu_l s_l(y_i,x,i) \right\}
\end{aligned}
举例来说,当 m = 3 时,除了 i =1 或者 i = n-1 ,每个矩阵 $M_i(x) \in\mathbb{R}^{3 \times 3}$, 如下图所示:
矩阵的形式类似于 HMM 中的转移矩阵,代表了状态之间转移的概率,其形式是这样的:
\begin{aligned}
M_1(x) &= \begin{bmatrix} M_1(y_0,y_1|x) & M_1(y_0,y_3|x) &M_1(y_0,y_3|x) \end{bmatrix} \\
\\
M_2(x) &=\begin{bmatrix}
M_2(y_1,y_1|x) & M_2(y_1,y_2|x) & M_2(y_1,y_3|x)\\
M_2(y_2,y_1|x) & M_2(y_2,y_2|x) & M_2(y_2,y_3|x)\\
M_2(y_3,y_1|x) & M_2(y_3,y_2|x) & M_2(y_3,y_3|x)
\end{bmatrix} \\
\\
M_i(x) \ &\mathbf{has \ the \ same \ form \ with} \ M_2(X), \ i = 3,...,n\\
\\
M_{n+1}(x) &=\begin{bmatrix}
M_{n+1}(y_1,y_n|x)& \\
M_{n+1}(y_2,y_n|x) & \\
M_{n+1}(y_3,y_n|x)&
\end{bmatrix} \\
\end{aligned}
这样,给定观测序列x,标记序列 y 的非规范化概率可以通过 n+1 个矩阵的乘积 $\prod_{i=1}^{n+1}M_i(y_{i-1},y_i|x)$ 表示,于是,条件概率 $P_w(y|x)$ 是:
\[P_w(y|x) = \frac{1}{Z_w(x)} \prod_{i=1}^{n+1} M_i(y_{i-1},y_i|x)\]
其中,$Z_w(x)$ 为规范化因子,是 n+1 个矩阵的乘积的 (start,stop) 元素:
\[Z_w(x) = \left \{M_1(x),M_2(x)…M_{n+1}(x) \right \} _{start}^{stop}\]
注意,$y_0 = start$ 与 $y_{n+1} = stop$ 表示开始状态与终止状态,规范化因子 $Z_w(x)$ 是以 start 为起点 stop 为终点通过状态的所有路径的非规范化概率 $y_1,y_2,…,y_n$ 之和。
这里的 M 矩阵像极了 HMM 中的转移概率矩阵,因为链式 CRF 中只有相邻两个节点间才有连接边。
参考:
http://www.hankcs.com/ml/conditional-random-field.html
条件随机场理论综述 paper
统计学习方法 book

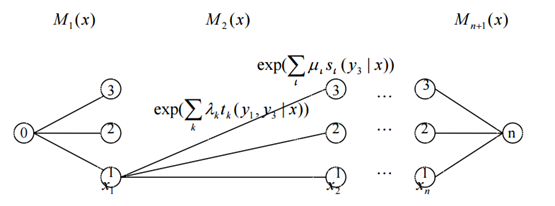

 浙公网安备 33010602011771号
浙公网安备 33010602011771号