高斯混合模型 GMM
本文将涉及到用 EM 算法来求解 GMM 模型,文中会涉及几个统计学的概念,这里先罗列出来:
- 方差:用来描述数据的离散或波动程度.
\[var(X) = \frac{\sum_{i=1}^N( X_i-\bar{X})^2}{N-1}\]
- 协方差:协方差表示了变量线性相关的方向,取值范围是 $[-\infty, +\infty]$,一般来说协方差为正值,说明一个变量变大另一个变量也变大;取负值说明一个变量变大另一个变量变小,取0说明两个变量没有相关关系.
\[cov(X,Y) = \frac{\sum_{i=1}^N( X_i-\bar{X})(Y_i-\bar{Y}) }{N-1}\]
- 相关系数:协方差可反映两个变量之间的相互关系及相关方向,但无法表达其相关的程度,皮尔逊相关系数不仅表示线性相关的方向,还表示线性相关的程度,取值$[-1,1]$,也就是说,相关系数为正值,说明一个变量变大另一个变量也变大;取负值说明一个变量变大另一个变量变小,取0说明两个变量没有相关关系,同时,相关系数的绝对值越接近1,线性关系越显著。
\[\rho_{XY} = \frac{cov(X,Y)}{\sqrt{DX}\sqrt{DX}}\]
- 协方差矩阵: 当 $X \in \mathbb{R}^n$ 为高维数据时,协方差矩阵可以很好的反映数据的性质,在协方差矩阵中,对角线元素反映了数据在各个维度上的离散程度,协方差矩阵为对角阵,非对角线元素反映了数据各个维度的相关性,其形式如下:
cov(x_1,x_1) & cov(x_1,x_2)&\cdots &cov(x_1,x_n) \\ cov(x_2,x_1) & cov(x_1,x_1)&\cdots &cov(x_1,x_1) \\
\vdots & \vdots & & \vdots & \\ cov(x_n,x_1) & cov(x_n,x_1)&\cdots &cov(x_n,x_n)
\end{bmatrix}\]
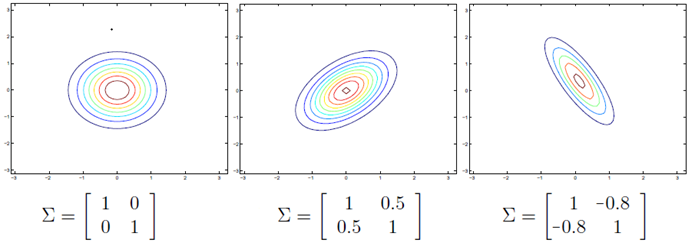
上图展示了二维情况下,使用不同的协方差矩阵时高斯分布的变化,左边代表不相关,中间为正相关,右边为负相关。
高斯分布
假设数据 $\mathbf{x} \in \mathbb{R}^n$ 服从参数为 $\mathbf{\mu},\mathbf{\Sigma}$ 的高斯分布:
\[ \mathcal{N}(\mathbf{x};\mu,\mathbf{\Sigma}) = \frac{1}{(2\pi)^{n/2}|\mathbf{\Sigma}|^{1/2}}\exp\left \{ -\frac{1}{2} (\mathbf{x}-\mu)^T\mathbf{\Sigma}^{-1}(\mathbf{x}-\mu) \right \}\]
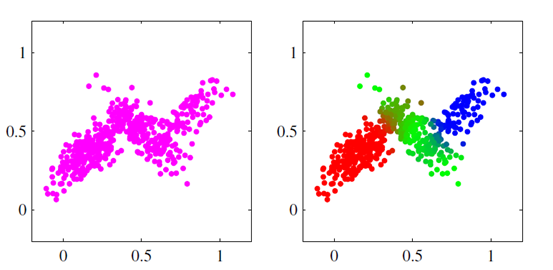
这里 $\mu$ 为均值, $\Sigma$ 为协方差矩阵,对于单个高斯分布,当给定数据集之后,直接进行 MLE 即可估计高斯分布的参数;但是有些数据集是多个高斯分布叠加在一起形成的,也就数据集是由多个高斯分布产生的,如下图所示三个高斯分布叠加在一起:
多个高斯分布叠加在一起便是混合高斯模型 GMM,GMM 的定义如下:
\[p(\mathbf{\mbox{x}}) = \sum_{k=1}^K \pi_k \mathcal{N}(\mathbf{\mbox{x}} | \mathbf{\mu}_k, \mathbf{\Sigma}_k)\]
这里 $K$ 表示高斯分布的个数, $\pi_k$ 代表 mixing coefficient ,且满足 $0 \le \pi_k \le 1,\sum_k\pi_k = 1$,其实这里 $p(\mathbf{x})$ 表示为 $K$ 个高斯分布的加权, $\pi_k$ 就是权重系数,如果把 GMM 用在聚类中,则样本 $\mathbf{x}$ 的类别即为 $\arg\max_k\pi_k$.
在 GMM 中,需要估计的参数为 $\pi_k, \mu_k, \mathbf{\Sigma}_k$,模型里每个观测数据 $\mathbf{x}$ 都对应着一个隐变量 $\mathbf{z} \in \mathbb{R}^K$,代表的即为类别变量, 且 $\mathbf{z}_k \in \left \{ 0,1\right \}$ ,一个样本可以属于多个类别,叠加起来概率为 1 ,这里显而易见有:
\[p(\mathbf{z}_k = 1) = \pi_k \]
则第 $k$ 个高斯分布可以表示为:
\[p(\mathbf{\mbox{x}}|z_k = 1) = \mathcal{N}(\mathbf{\mbox{x}} | \mathbf{\mu}_k, \mathbf{\Sigma}_k)\]
如果已知 $\mathbf{x}$ 所属的分布 $k$ ,则可把上式写成向量形式:
\[p(\mathbf{x}|\mathbf{z}) = \mathcal{N}(\mathbf{\mbox{x}} | \mathbf{\mu}_k, \mathbf{\Sigma}_k)\]
因此完全数据的密度函数为:
\[p(\mathbf{\mbox{x}}) = \sum_{\mathbf{\mbox{z}}} p(\mathbf{\mbox{z}}) p(\mathbf{\mbox{x}} | \mathbf{\mbox{z}}) = \sum_{k=1}^K \pi_k \mathcal{N}(\mathbf{\mbox{x}} | \mathbf{\mu}_k, \mathbf{\Sigma}_k)\]
单个样本推倒完成,接下来给定观测数据集 $X$,对应的完全数据集为 $\left\{ X,Z\right\}$ ,此时 $Z$ 是不可见的,形式如下:
\[X = \begin{bmatrix} - \mathbf{x}_1^T-\\ -\mathbf{x}_2^T -\\ \vdots \\ -\mathbf{x}_N^T -\\\end{bmatrix} \ \ Z = \begin{bmatrix} - \mathbf{z}_1^T-\\ -\mathbf{z}_2^T -\\ \vdots \\ -\mathbf{z}_N^T -\\\end{bmatrix}\]
对于该 GMM 的参数就采用 EM 算法来求解了,完全数据的联合分布为:
\[p(\mathbf{X,Z} | \mathbf{\mu, \Sigma, \pi}) = \prod_{n=1}^N \left \{ \sum_{k=1}^K \pi_k \mathcal{N}(\mathbf{\mbox{x}}_n \vert \mathbf{\mu}_k, \mathbf{\Sigma}_k) \right \}\]
写成对数似然函数的形式:
\[\ln p(\mathbf{\mbox{X,Z}} | \mathbf{\mu, \Sigma, \pi}) = \sum_{n=1}^N \ln \left \{ \sum_{k=1}^K \pi_k \mathcal{N}(\mathbf{\mbox{x}}_n | \mathbf{\mu}_k, \mathbf{\Sigma}_k) \right \}\]
下面便是EM 算法求解 GMM 的过程:
E步: 使用参数 $\theta^{old}=(\pi^{old},\mu^{old},\mathbf{\Sigma}^{old})$ ,计算每个样本 $x_n$ 对应隐变量 $z_n$ 的后验分布:
\begin{aligned}
\gamma(z_{nk})=p(z_n = k|\mathbf{x}_n;\mathbf{\mu}^{old},\mathbf{\Sigma}^{old})
&=\frac{p(z_{nk} = 1)p(\mathbf{x_{nk}}|z_{nk} = 1)}{\sum_{j=1}^Kp(z_{nj} = 1)p(\mathbf{x_n}|z_{nj} = 1)}\\
&= \frac{ \pi_k^{old} \mathcal{N}(\mathbf{\mbox{x}}_n | \mathbf{\mu}_k^{old}, \mathbf{\Sigma}_k^{old})} {\Sigma_{j=1}^K\pi_j^{old} \mathcal{N}(\mathbf{\mbox{x}}_n | \mathbf{\mu}_j^{old}, \mathbf{\Sigma}^{old}_j)}
\end{aligned}M步:便是极大化 Q 函数的计算,这里 Q 函数有非常漂亮的形式:
\begin{aligned}
\mathcal{Q} (\mathbf{\theta}, \mathbf{\theta}^{\mbox{old}})
&= \sum_{Z} p(Z | X,\theta^{old}) \ln p(X, Z | \theta)\\
&= \sum_{Z} p(Z | X,\theta^{old}) \ln p(X| Z ,\theta)P(Z|\theta)\\
&=\sum_{n= 1}^N \sum_{k=1}^K\gamma(z_{nk})\left \{ \ln \pi_k +\ln\mathcal{N}(\mathbf{x}_n|\mathbf{\mu}_k ,\mathbf{\Sigma}_k) \right \}\\
\end{aligned}得到下一步迭代的参数:
\[\theta^{new}=\arg\max_{\theta}\mathcal{Q} (\mathbf{\theta}, \mathbf{\theta}^{\mbox{old}}) \]
对 Q 函数求导,另倒数得 0 ,即可求得下一次迭代的参数值,这里省去计算过程,只给出结果:
\begin{aligned}
\mathbf{\mu}_k^{new} &= \frac{1}{N_k}\sum_{n=1}^N\gamma(z_{nk})\mathbf{x}_n\\
\mathbf{\Sigma}_k^{new} &= \frac{1}{N_k}\sum_{n=1}^N\gamma(z_{nk})(\mathbf{x}_n-\mathbf{\mu}_k^{new})(\mathbf{x}_n-\mathbf{\mu}_k^{new})^T \\
\mathbf{\pi}_k^{new} &= \frac{N_k}{N}
\end{aligned}
其中:
\[N_k = \sum_{n=1}^N \gamma(z_{nk})\]
这便是完整的 GMM 推倒过程,理解的不是很好,有机会继续深入。
参考:
Pattern Reconginition and Machine Learning
http://www.zhihu.com/question/20852004
http://www.cnblogs.com/nsnow/p/4758202.html
http://alexkong.net/2014/07/GMM-and-EM/
http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html
http://www.cnblogs.com/ooon/p/5787995.html