递归神经网络（Recurrent Neural Networks，RNN）
在深度学习领域，传统的多层感知机（MLP）具有出色的表现，取得了许多成功，它曾在许多不同的任务上——包括手写数字识别和目标分类上创造了记录。甚至到了今天，MLP在解决分类任务上始终都比其他方法要略胜一筹。尽管如此，大多数专家还是会达成共识：MLP可以实现的功能仍然相当有限。究其原因，人类的大脑有着惊人的计算功能，而“分类”任务仅仅是其中很小的一个组成部分。我们不仅能够识别个体案例，更能分析输入信息之间的整体逻辑序列。这些信息序列富含有大量的内容，信息彼此间有着复杂的时间关联性，并且信息长度各种各样。这是传统的MLP所无法解决的，RNN 正式为了解决这种序列问题应运而生，其关键之处在于当前网络的隐藏状态会保留先前的输入信息，用来作当前网络的输出。
许多任务需要处理序列数据，比如Image captioning, speech synthesis, and music generation 均需要模型生成序列数据，其他领域比如 time series prediction, video analysis, and musical information retrieval 等要求模型的输入为序列数据，其他任务比如 机器翻译，人机对话，controlling a robot 的模型要求输入输出均为序列数据。 RNN 模型可以用来处理序列数据， RNN 包含了大量参数，且难于训练（时间维度的 vanishing/exploding），所以出现一系列对 RNN 优化 ，比如网络结构、求解算法与并行化。今年来 bidirectional RNN （BRNN）与 LSTM 在 image captioning, language translation, and handwriting recognition 这几个方向上有了突破性进展 。下面从 RNN 开始来逐一介绍这些网络模型。
RNN 的结构不同于 MLP ，输入层与来自序列中上一元素隐层的信号共同作用到当前的隐藏层，如下图所示：
下图能更清楚的展示 RNN 的结构：
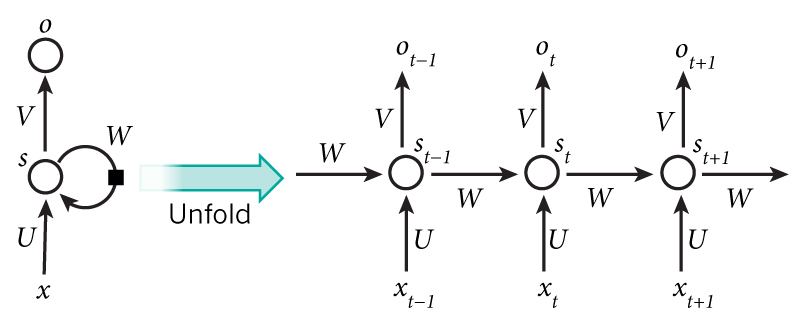看下面关于 RNN BP分析之前，请确保之前看过 多层感知机及其BP算法（Multi-Layer Perceptron），此文为 RNN BP 的基础，现在来看 RNN 的 BP 算法，对于长度为 $T$ 的序列 $x$ ，RNN 的输入层大小为 $I$ ，隐层大小为 $H$ ，输出层大小为 $K$ ，可以得到上图中三个矩阵的维度分别为 ： $U \in \mathbb{R}^{I \times H} , W \in \mathbb{R}^{H \times H} , V \in \mathbb{R}^{H \times K} $ ，这里 $x^t$ 代表序列第 $t$ 项 的输入， $a^t$ 代表第 $t$ 项隐层的输入，$b^t$ 代表对 $a^t$ 做非线性激活也即为神经网络的输出 ，这里 $a^t$ 由输入层 $x^t$ 与 上一层隐层的输出 $b^{t-1}$ 共同决定：
\[a_h^t =\sum_iw_{ih}x_i^t +\sum_{h'}w_{h'h}b_{h'}^{t-1}\]
\[b_h^t = f(a_h^t)\]
这里 序列从状态 $t=1$开始，一般设置 $b^0 = 0 $ 即可，接下来将隐层传导至输出层即可,通常 RNN 的输出层采用与传统 MLP 的类似的 $softmax$ 来进行分类任务.即输出层的输出为：
\[a_k^t = \sum_hw_{hk}b_h^t\]
\[y_k^t = \frac{e^{a_k^t}}{\sum_j e^{a_j^t}}\]
注意 RNN 中由于输入时叠加了之前的信号，所以反向传导时不同于传统的 MLP ，因为对于时刻 $t$ 的输入层，其残差不仅来自于输出，还来自于之后的隐层入下图所示：
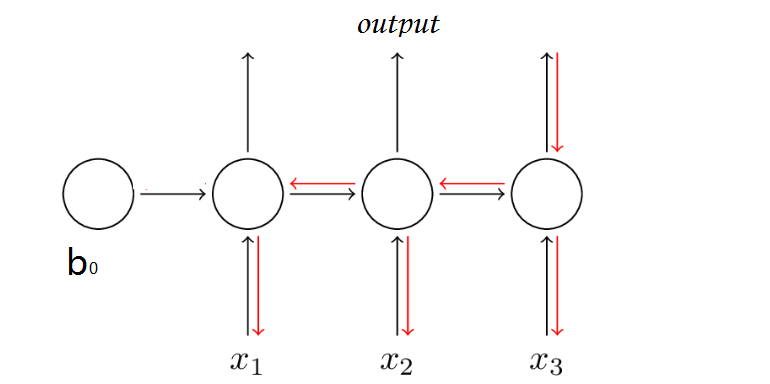
时刻 $t$ ，RNN 输出层的算残差项同 MLP 为 $ \delta_k^t = y_k^t-z^t_k$，由于前向传导时隐层需要接受上一个时刻隐层的信号，所以反向传导时根据 BPTT 算法，隐层还需接收下一时刻的隐层的反馈：
\[\delta_h^t = f'(a_h^t) \left (\sum_k\delta_k^tw_{hk} + \sum_{h'} \delta^{t+1}_{h'}w_{hh'} \right )\]
当序列长度为 $T$ ，则残差 $\delta^{T+1}$ 均为 0 。并且整个网络其实就只有一套参数 $U$、$V$、$W$ ， 对于时刻 $t$ 其倒数分别为：
\[U: \ \frac{\partial O}{\partial w_{ih}}= \frac{\partial O}{\partial a_h^t}\frac{\partial a_h^t}{\partial w_{ih}}=\delta_h^tx_i^t\]
\[V: \ \frac{\partial O}{\partial w_{hk}}= \frac{\partial O}{\partial a_k^t}\frac{\partial a_k^t}{\partial w_{hk}}=\delta_k^tb_h^t\]
\[W: \ \frac{\partial O}{\partial w_{h'h}}= \frac{\partial O}{\partial a_h^t}\frac{\partial a_h^t}{\partial w_{h'h}}=\delta_k^tb_{h'}^t \]
为了方便表示，写成统一的形式（假设对输入层有 $x_i^t = a_i^t =b_i^t$）：
\[\frac{\partial O}{\partial w_{hij}}= \frac{\partial O}{\partial a_j^t}\frac{\partial a_j^t}{\partial w_{ij}}=\delta_j^tb_i^t\]
最后，由于 RNN 的递归性 ，对于时刻 $t = 1,2,...,T$ ,将其进行求和即可，下面为最终得 RNN 网络的关于权重参数的导数：
\[\frac{\partial O}{\partial w_{ij}}= \sum_t\frac{\partial O}{\partial a_j^t}\frac{\partial a_j^t}{\partial w_{ij}} = \sum _t \delta_j^tb_i^t\]
Bidirectional RNNs
RNN 中对于当前时刻 t 通常会考虑之前时刻的信息而没有考虑下文的信息，Bidirectional RNNs 克服了这一缺点，其引入了对下文的考虑，其结构如下：
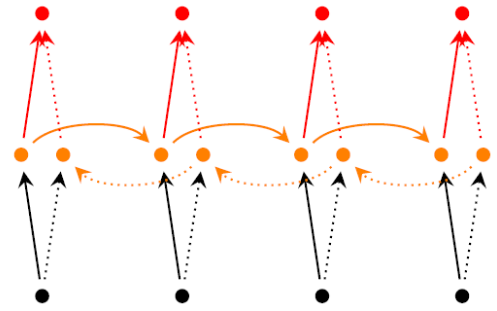
可见 BRNN 引入了一套额外的隐层，但是输入与输出层是共享的，多了一个隐层意味着多了三套参数分别为 $U'$、$V'$、$W'$ 。BRNN 的训练算法类似于 RNN ，forward pass 的过程如下：
backward pass 的过程如下：
计算完残差后，分别对前向参数 $U$、$V$、$W$ 后向参数 $U'$、$V'$、$W'$ 求导即可，至此 BRNN 的训练算法介绍完毕， 目前 ，BRNN 在 NLP 的序列标注任务中取得了极大的成功。
