（二）深入梯度下降(Gradient Descent)算法
一直以来都以为自己对一些算法已经理解了，直到最近才发现，梯度下降都理解的不好。
1 问题的引出
对于上篇中讲到的线性回归，先化一个为一个特征θ1，θ0为偏置项，最后列出的误差函数如下图所示：
手动求解
目标是优化J(θ1)，得到其最小化，下图中的×为y(i)，下面给出TrainSet，{(1,1),(2,2),(3,3)}通过手动寻找来找到最优解，由图可见当θ1取1时，
与y(i)完全重合，J(θ1) = 0
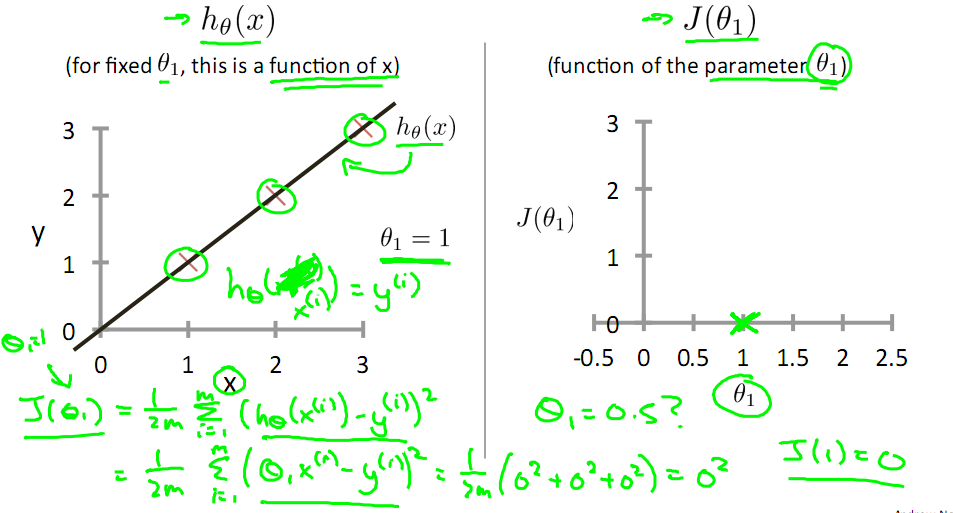
下面是θ1的取值与对应的J(θ1)变化情况
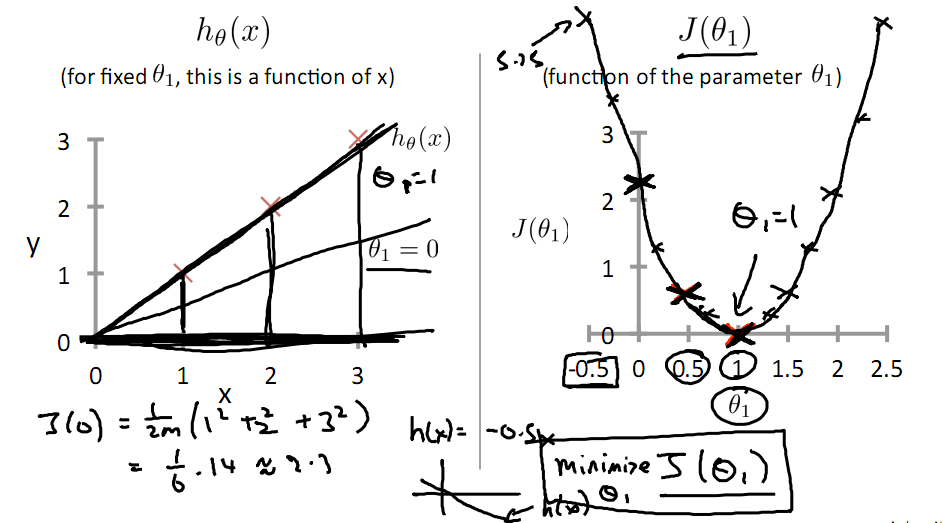
由此可见，最优解即为0，现在来看通过梯度下降法来自动找到最优解，对于上述待优化问题，下图给出其三维图像，可见要找到最优解，就要不断向下探索，使得J(θ)最小即可。
2 梯度下降的几何形式
下图为梯度下降的目的，找到J（θ）的最小值。
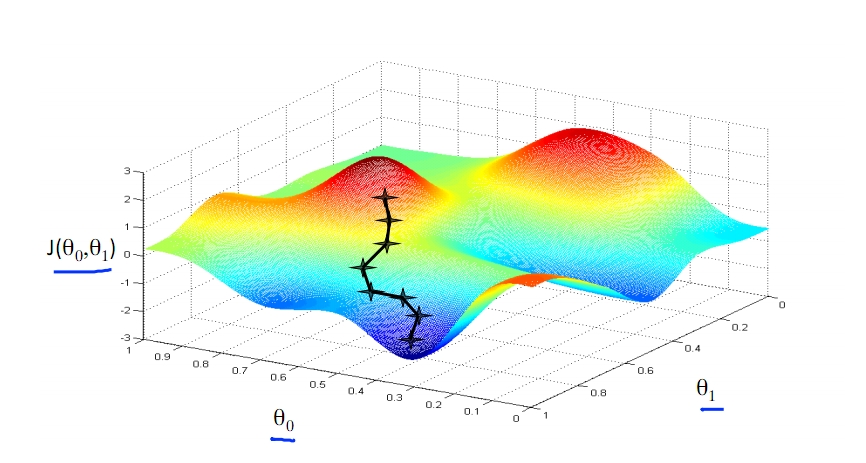
其实，J(θ)的真正图形是类似下面这样的，因为其是一个凸函数，只有一个全局最优解，所以不必担心像上图一样找到局部最优解
直到了要找到图形中的最小值之后，下面介绍自动求解最小值的办法，这就是梯度下降法
对参数向量θ中的每个分量θj，迭代减去速率因子a* (dJ(θ)/dθj)即可，后边一项为J(θ)关于θj的偏导数
3 梯度下降的原理
导数的概念
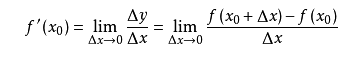
由公式可见，对点x0的导数反映了函数在点x0处的瞬时变化速率，或者叫在点x0处的斜度。推广到多维函数中，就有了梯度的概念，梯度是一个向量组合，反映了多维图形中变化速率最快的方向。
下图展示了对单个特征θ1的直观图形，起始时导数为正，θ1减小后并以新的θ1为基点重新求导，一直迭代就会找到最小的θ1，若导数为负时，θ1的就会不断增到，直到找到使损失函数最小的值。
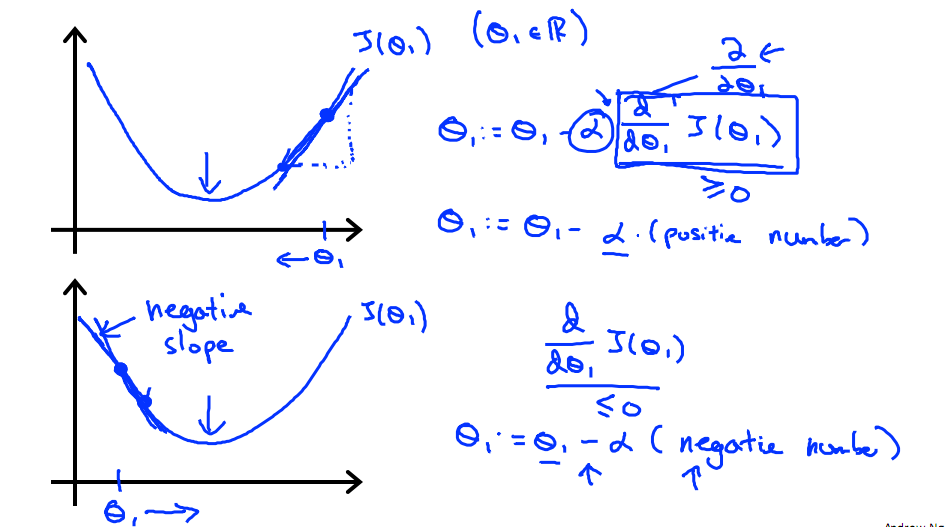
有一点需要注意的是步长a的大小，如果a太小，则会迭代很多次才找到最优解，若a太大，可能跳过最优，从而找不到最优解。
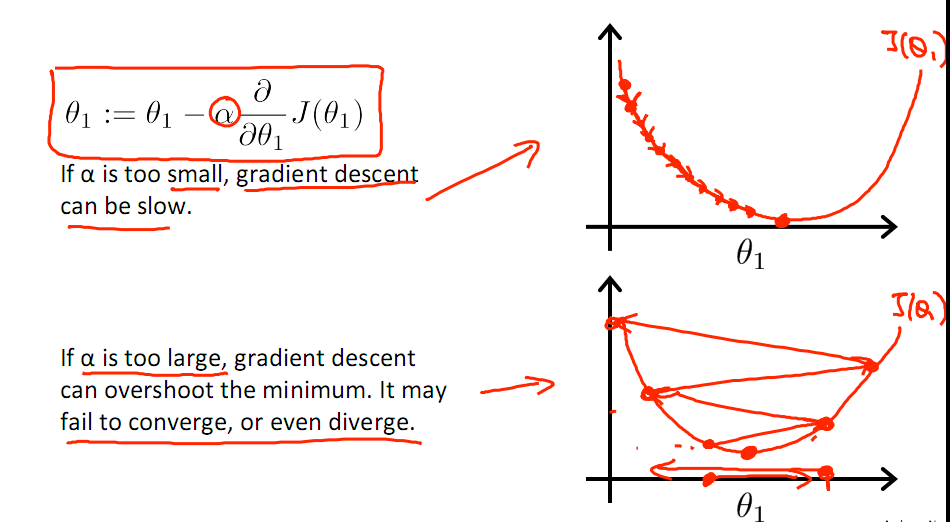
另外，在不断迭代的过程中，梯度值会不断变小，所以θ1的变化速度也会越来越慢，所以不需要使速率a的值越来越小
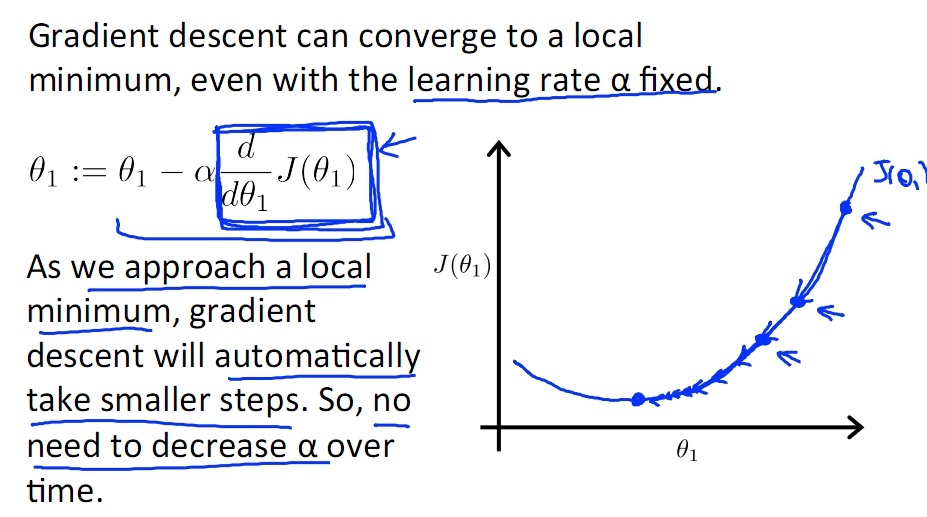
下图就是寻找过程
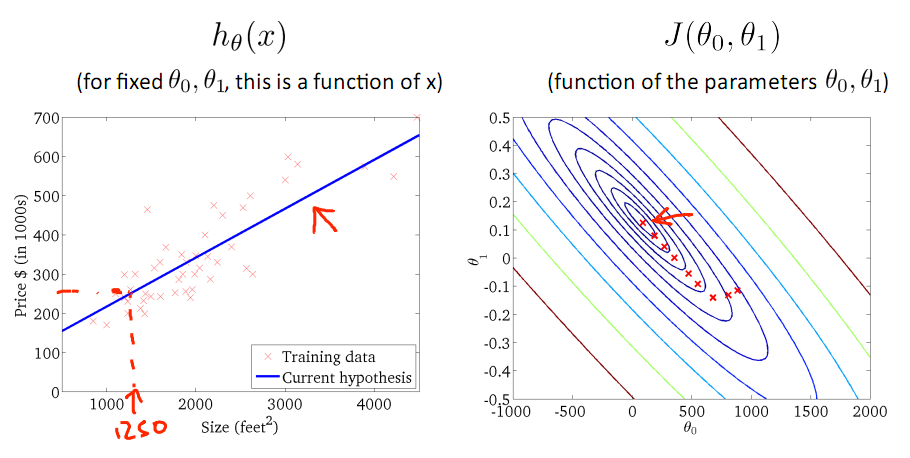
当梯度下降到一定数值后，每次迭代的变化很小，这时可以设定一个阈值，只要变化小鱼该阈值，就停止迭代，而得到的结果也近似于最优解。
若损失函数的值不断变大，则有可能是步长速率a太大，导致算法不收敛，这时可适当调整a值
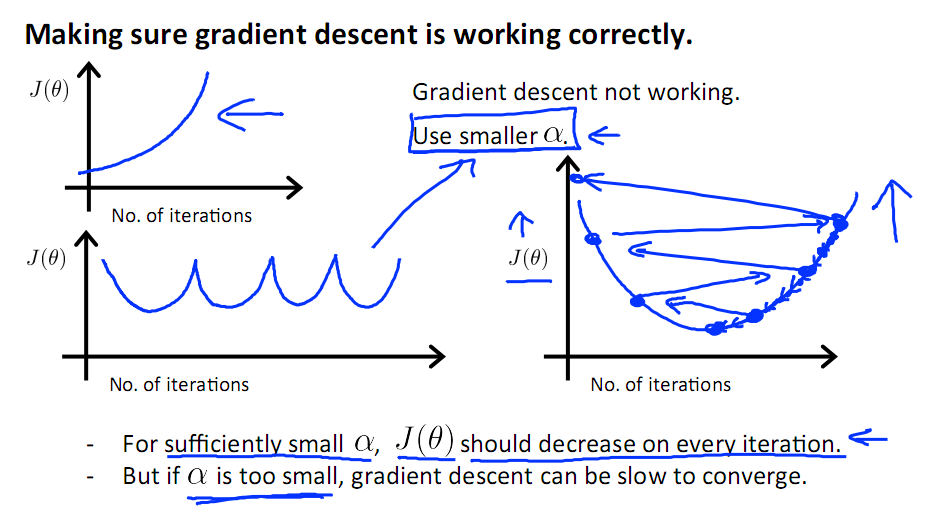
为了选择参数a，就需要不断测试，因为a太大太小都不太好。
如果想跳过的a与算法复杂的迭代，可以选择 Normal Equation。
4 随机梯度下降
对于样本数量额非常之多的情况，Batch Gradient Descent算法会非常耗时，因为每次迭代都要便利所有样本，可选用Stochastic Gradient Descent 算法，需要注意外层循环Loop，因为只遍历一次样本，不见得会收敛。
随机梯度算法就可以用作在线学习了，但是注意随机梯度的结果并非完全收敛，而是在收敛结果处波动的，可能由非线性可分的样本引起来的：
可以有如下解决办法：（来自MLIA）
1. 动态更改学习速率a的大小，可以增大或者减小
2. 随机选样本进行学习
