计算机科学速成课(Crash Course Computer Science)笔记:晶体管的应用、CPU
早期计算机的发展:
算盘 - 步进式 - 计算表 - 差分机 - 打孔制表机 - 电子计算机
机械继电器:mechanical relay
1945年,哈佛马克 1:使用继电器,用电磁效应,控制机械开关,缺点为有磨损和延迟
真空管(vaccum tube)的应用:计算机从机电走向电子
1943年,巨人:第一个可编程的电子计算机,编程方法是把几百根电线插入插板
1947年,贝尔实验室发明发明了晶体管(transistor)
晶体管:通过其中的“gate”改变半导体材料的导电性
如今计算机中的晶体管都小于50纳米
晶体管:泛指一切以半导体为基础的单一元件
为什么选择使用二进制?
状态越多,信号越难以区分;临近的信号可能会混杂在一使得情况难以区分
有一个专门处理真假的数学分支的存在,已经解决了所有法则和运算:布尔代数(Boolean Algebra),在布尔代数中,变量true和false进行逻辑操作。
三个基本操作:NOT:翻转布尔值 AND OR
将晶体管类比为水龙头,gate是控制水流的龙头
在not中我们将上面看做输出,左侧看做输入
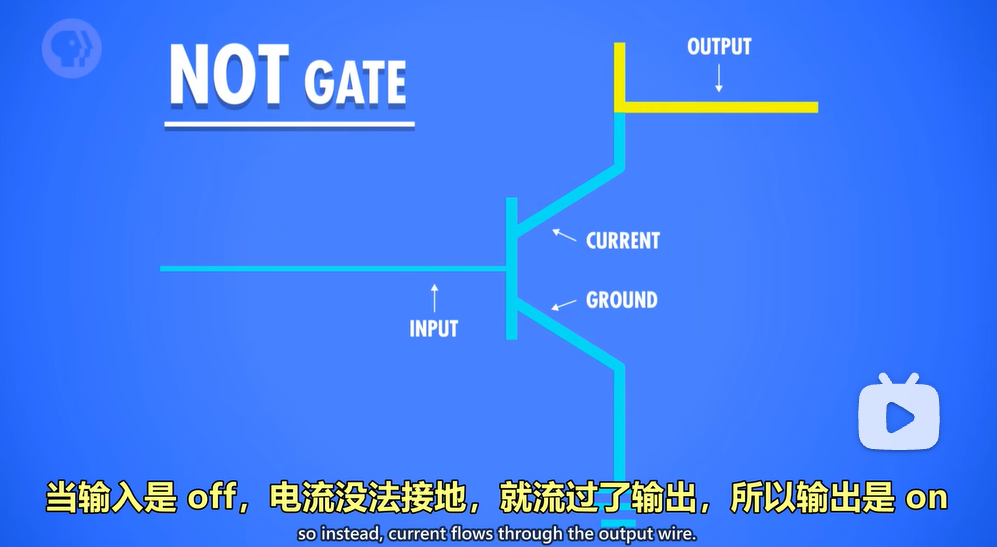
and gate 为两个二极管串联
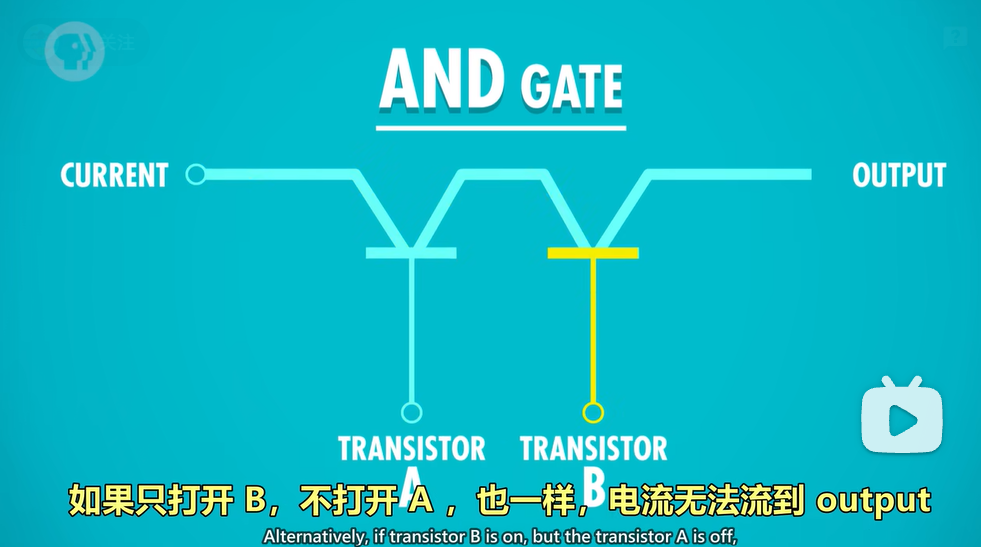
or gate:
有两个输入,只要两个输入中有一个是true,则输出为true。
代入到实际问题去理解就是,在输入的两个东西中(比如两个描述,或者两个问题)可以将or运算理解为“或”,即两个描述中只要有一个是符合事实的(“true”),则得到的结果(输出)也应当是“true”
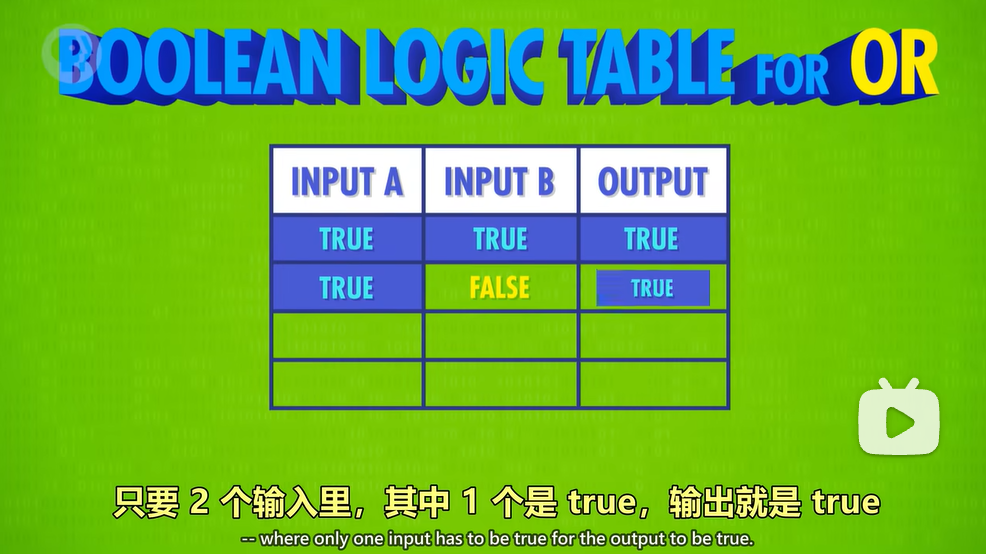
区分于and gate,or gate 是两个二极管并联。
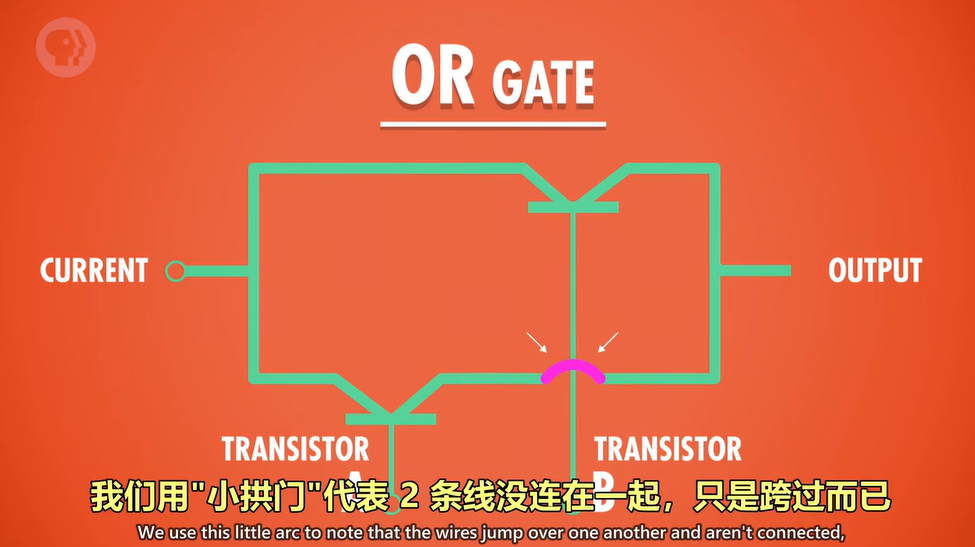
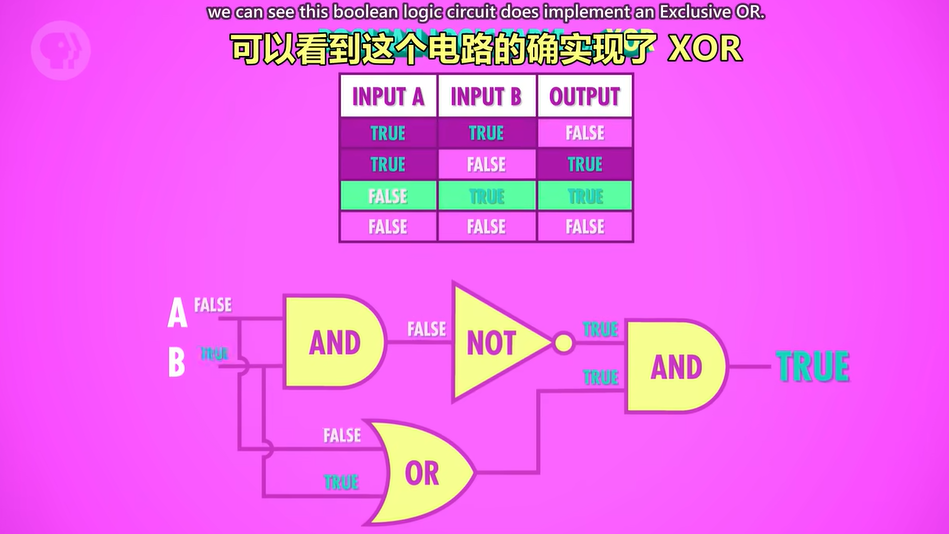
还有一种叫“异或”的操作,XOR。
区分于OR,当两个输入都是TRUE时,XOR的输出为FALSE。

XOR的表示:
有三种情况与OR相同,所以其中一定有一个OR,然后尝试去表示TRUE&TURE=FALSE的情况。
注意此处我们使用了“抽象”的方法,没有再使用transistor去表示,而是使用了之前的三种逻辑运算。
“8位”:即计算机是以8位为一组进行数据处理,所以8位的电脑游戏只有256种颜色。
现在的电子产品都是32位或者64位,这也是现在网络上的图片相当清晰的原因。
一般用第一位表示正负,用剩余31位I表示数的大小。
1 bytes(字节) = 8 bits(位)
计算机必须给内存中的每一个位置做标记,称为“位址”(addresses)
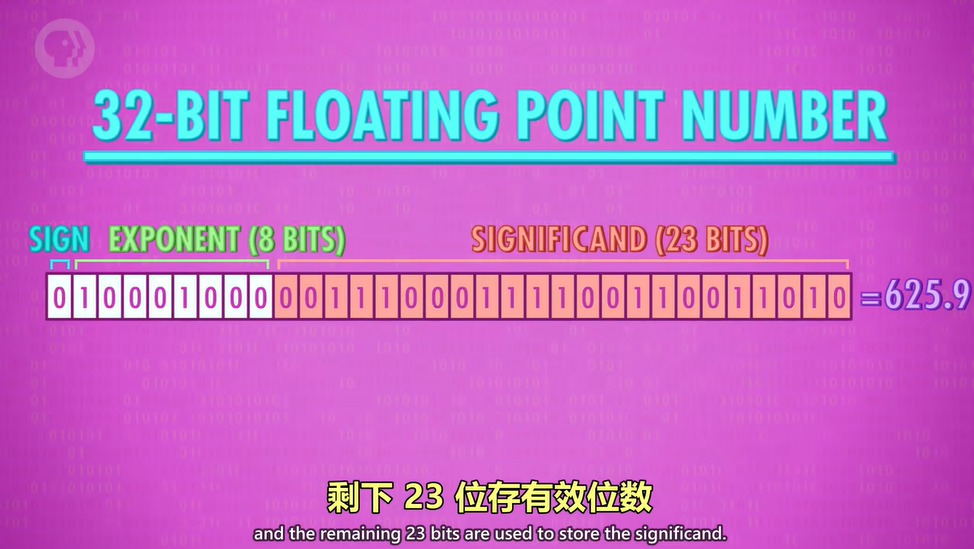
浮点数的存储:有多种方法
其中一种使用的是类似于科学计数法的方法
字母的存储:
ASCII:互用性(interoperability),但缺点是它为英文设计的,其他的语言(如中文、日文)需要自己编码,而这些编码通常不是国际通用的。
在这种情况下,Unicode诞生了。
第五集:
ALU(arithmetic and logic unit)
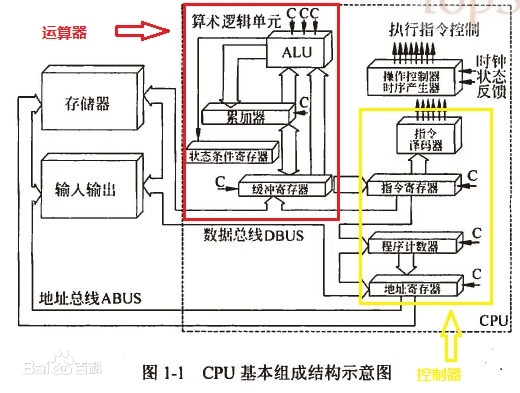
ALU是计算机内负责运算的组件,是CPU的一部分。
ALU包含两部分:算术单元和逻辑单元(Arithmetic Unit 和 Logic Unit)
1. 算术单元(arithmetic unit)
负责计算机内的所有数字操作
由半加器、全加器组成
底层实现是晶体管,抽象为用逻辑门表示
基础:两数相加
最简单的加法电路:将两个bits(0/1)加起来。
XOR逻辑门可以完全对应二进制加法的个位,同时我们用AND来表示十位
此时得到的为半加器(half adder),如下图
半加器
half adder虽然能得到进位值,但它不能处理进位。
进位:carry
总和:sum
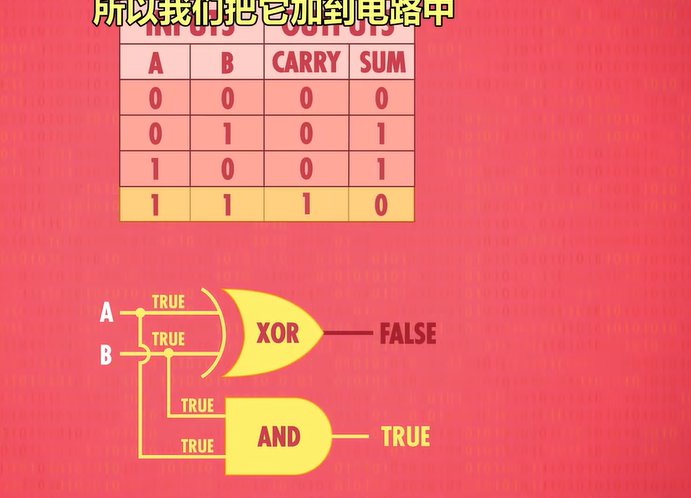
当我们在计算除了个位之外的高位运算时,除了将两数的该位相加之外,还需要再加上上一位的进位(如果有的话),所以此时我们是在将三个数相加。
此时我们使用一个全加器(full adder)去处理这种三个数(在下图中表示为A、B、C)相加的情况。
全加器
全加器的思路是先计算本位的加法,之后再利用OR逻辑门去计算进位的情况。先计算两数AB相加,能得到1、0、10三种情况。如果此时有进位,则此时A+B所得的sum一定为0,则第二次半加最大为0+1=1。三数相加,最大是1+1+1=11,进位最大就是1,不可能再进位到第三位,所以将两次半加所得的carry做OR处理,只要两个半加中有一次出现了进位,则最后就会有进位。
注意,全加器不是用来处理多位数的加法的,而是用来处理多位数的非个位的某一位的加法的;半加器是处理个位加法的。
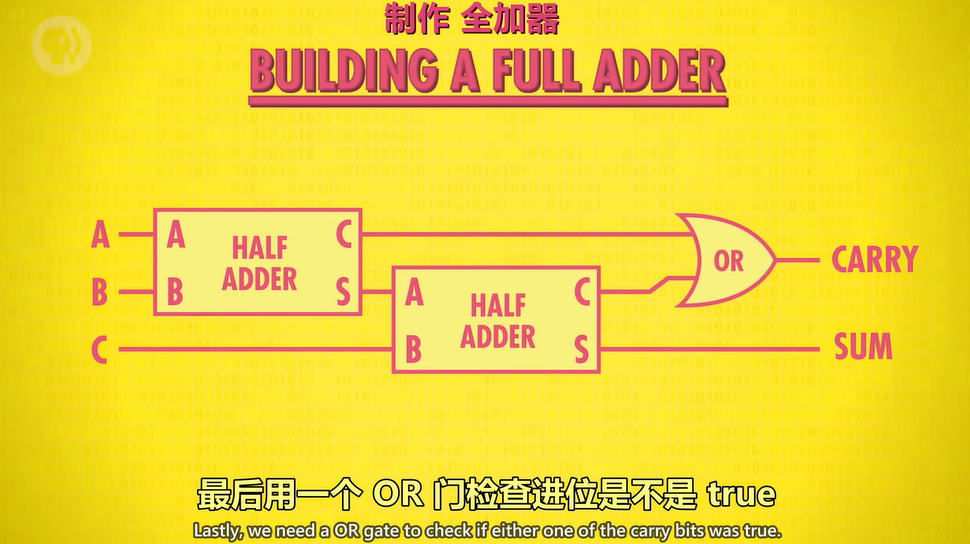
到现在,我们可以再将半加器和全加器进行抽象,制作8位加法运算器。
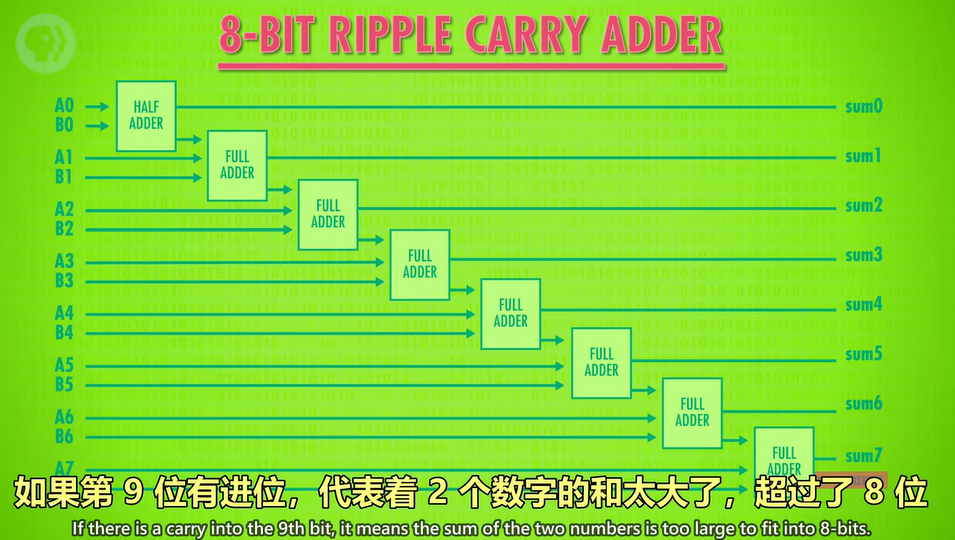
ps. 有人在MC中利用红石制作了加法器:https://www.bilibili.com/video/BV1Fk4y1k7VZ?share_source=copy_web
如果超出8位,就是导致overflow。
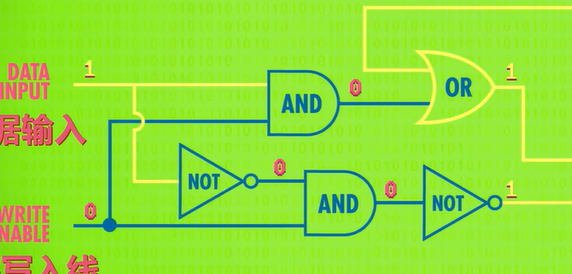
上面绿色背景的图片所展示的是一种比较原始的多位加法器,称为“波纹进位加法器”或“脉动进位加法器”(ripple-carry adder)。“波纹”形象地描述了进位信号依次向前传递的情形。
如果增加运算位数,一方面需要更多的逻辑门,另一方面由于高位的计算必须等待低位的进位输出信号被计算出来才能开始,在进行大规模数据计算时会显著增加运算时间。
所以,当今的计算机使用的是另一种有些不同的加法运算器:
超前进位加法器('carry-look-ahead' adder)
其具体原理请看本博的另一篇随笔:超前进位加法器原理详解
算术单元支持的其他运算(如图)

2. 逻辑单元
执行逻辑操作,如 NOT、AND、OR 等操作,以及做简单的数值测试(如判断某数是否为负)。
第六集:
寄存器与内存
原来我们所做的东西都是让电单向流动的,
现在我们将逻辑门的输出与其中一个输入连在一起,可以得到一个存储0/1的器件。
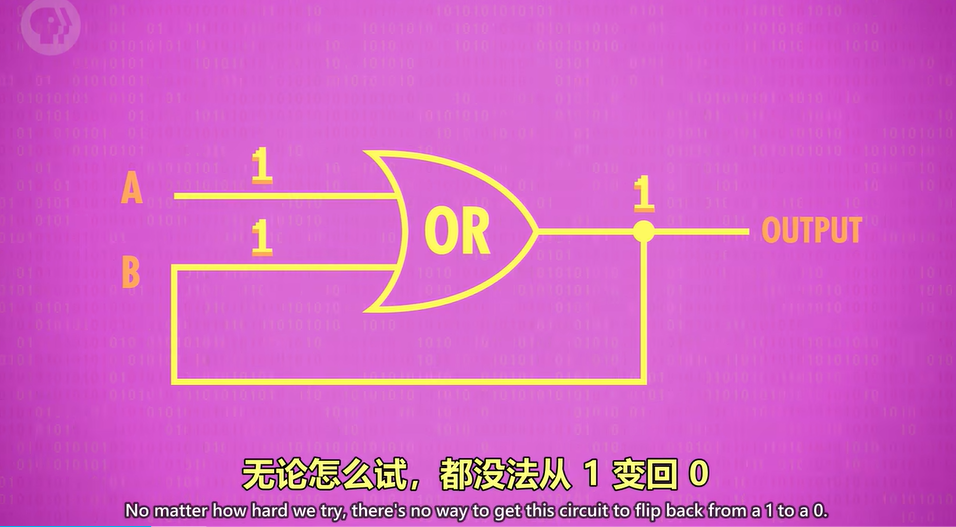
or gate可以用来存储1
and gate可以用来存储0

现在,我们将它们连接起来,做成了一个锁存器:
锁存器
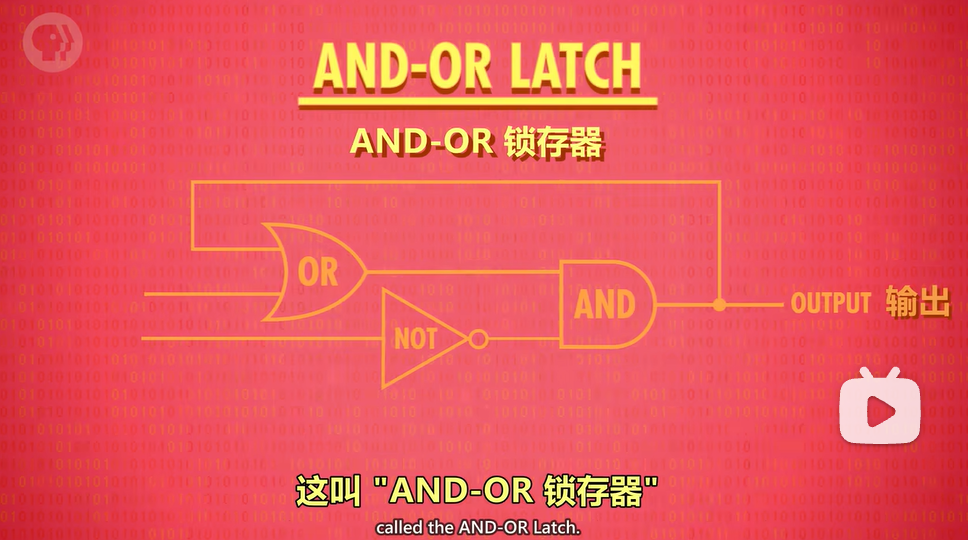
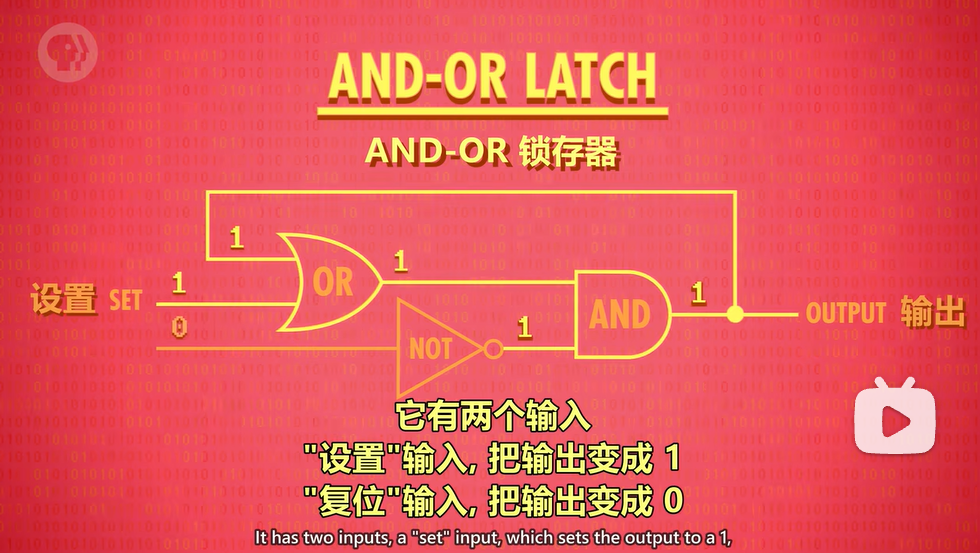
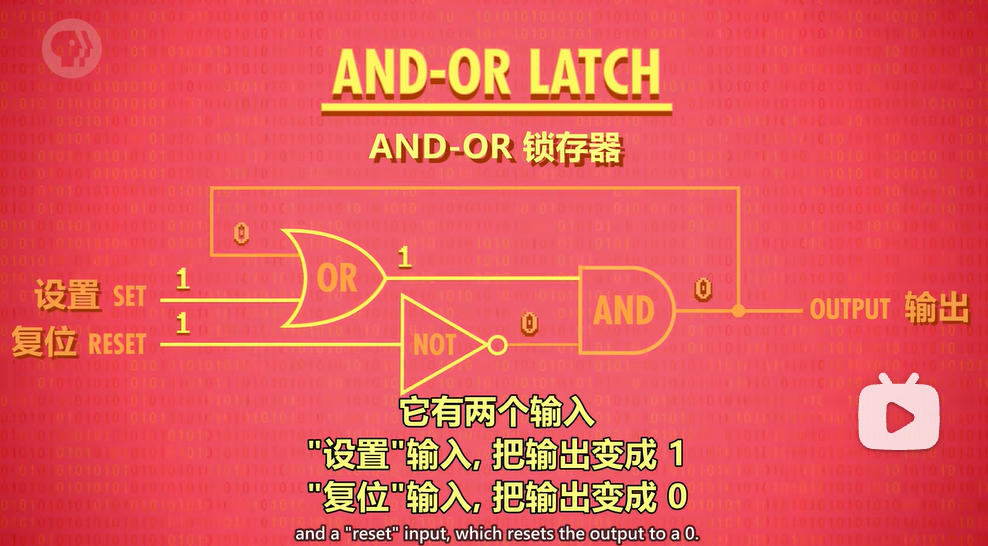
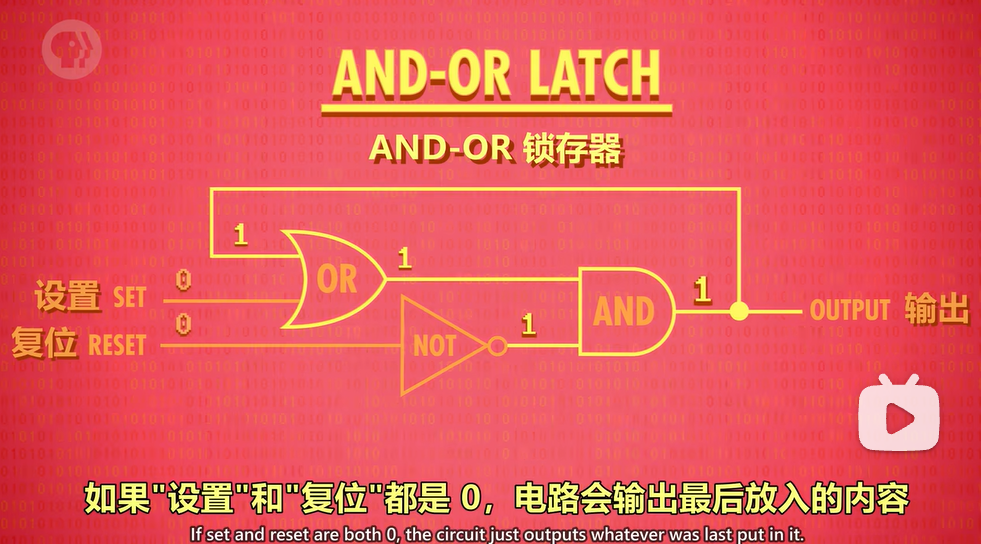

上图为不同输入情况(左)对应读取出的输出情况(右)
若输入为01,则此时不能确定上方逻辑门的输出。
为什么输入00会输出最后放入的内容?
因为or gate上方与输出相连的输入(灰色圆点标出处)是不会随剩余两个输入的改变而改变的。
门锁
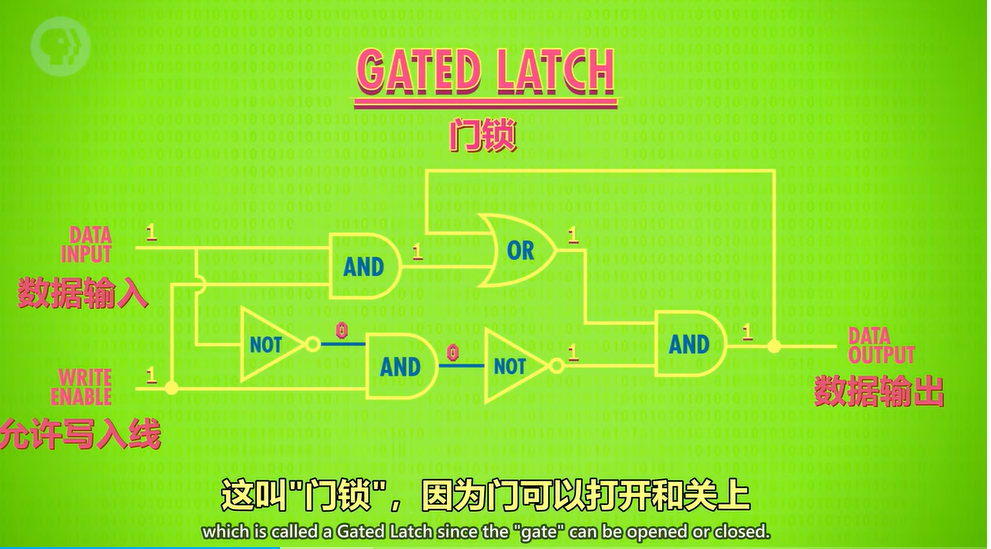
注意,门锁不是上图结构的名称,对比上文中锁存器的图片可知,上图为“门锁锁存器”,而“门锁”为下图中蓝绿色线条标出的部分线路。
单个锁存器(latches)只能存储一个bit。一组锁存器(latches)称为寄存器(register)。
寄存器
寄存器能存一个数字,数字的位数称为“位宽”(width)。
现在的计算机大多使用为64位宽的寄存器。
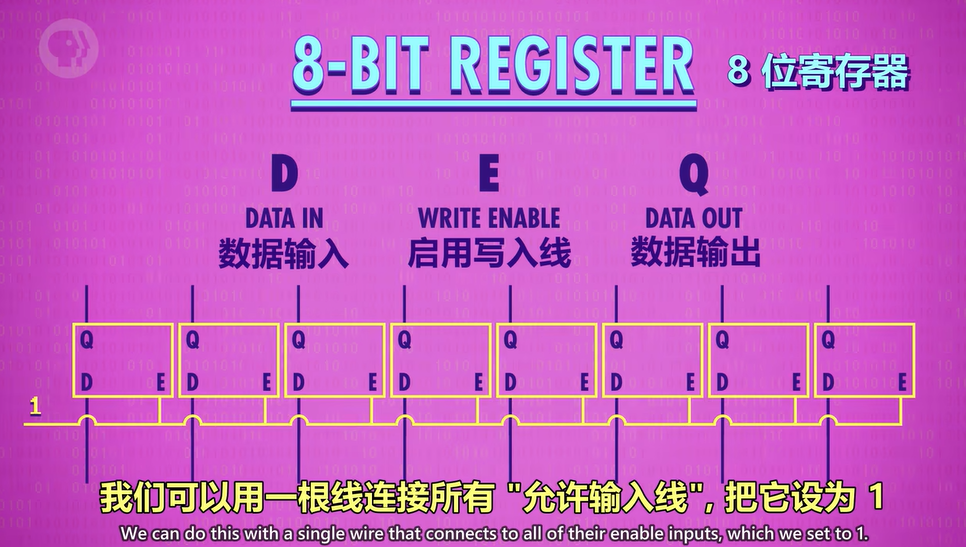
即使我们可以通过一根线来控制一个寄存器中所有的锁存器,每个锁存器的输入和输出都需要2根单独的线。
随着寄存器位宽的增加,我们需要非常多条线。
因此,我们选择使用矩阵去解决。
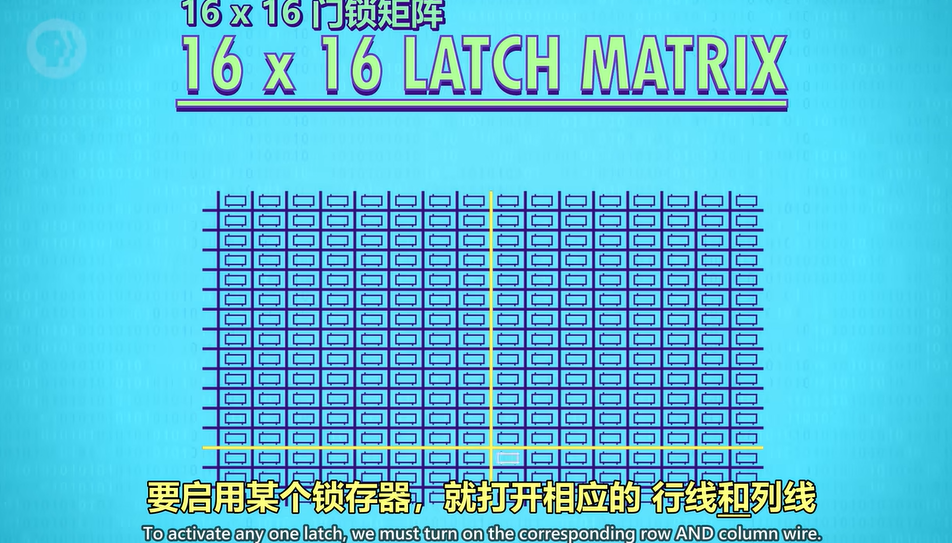
行线和列线在单个锁存器中用一个and gate 连接。
使用一条允许写入线去连接了一个矩阵中的所有的锁存器。(可以看到write enable下方的线的末端是一串虚线)
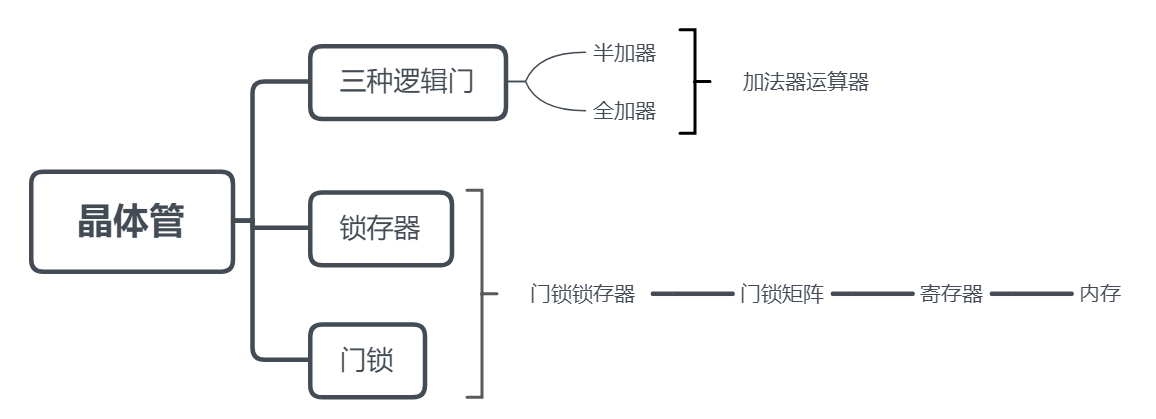
小结:使用晶体管,我们可以做些什么?
见下方的思维导图。
第七集:
CPU(central processing unit)
负责执行(execute)程序。
程序由操作(operation)组成,这些操作叫做“指令”(instruction)。
数学指令会被交由ALU处理,内存指令中,CPU会与内存通信进行读写操作。
微架构(Microarchitecture):
指令架构规定了CPU执行什么样的指令、执行结果应该是怎样的,但没有规定CPU内部实现指令执行的方式。
相对于指令架构,CPU内部的硬件结构就是CPU微架构。
CPU的工作:
取指令(fetch) - 解码(decode) - 执行(execute)
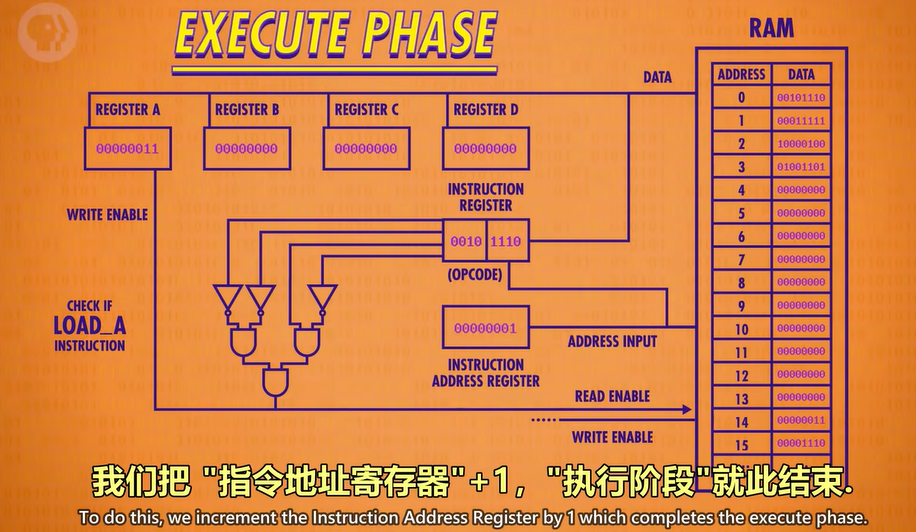
在此处我们以LOAD_A的指令为例子去解释CPU是如何工作的。
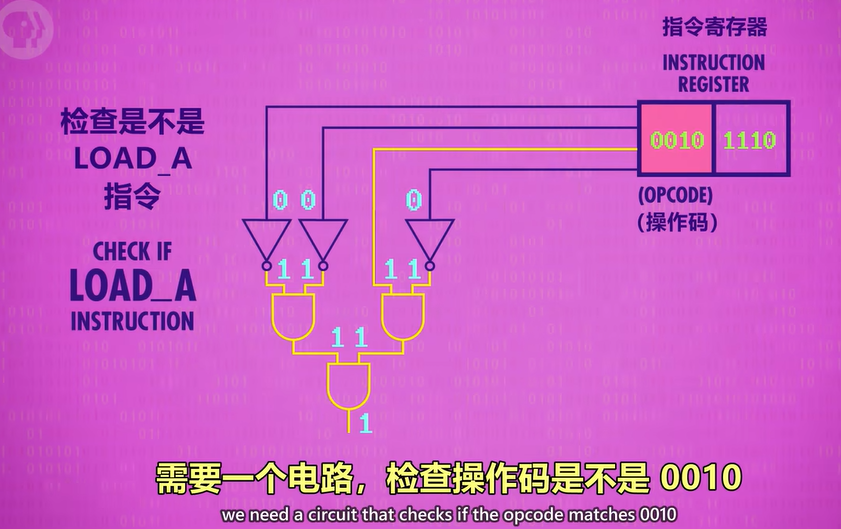
在CPU中,不止是LOAD_A(如下图),每一种指令都有自己所对应的实体电路去运行该指令。
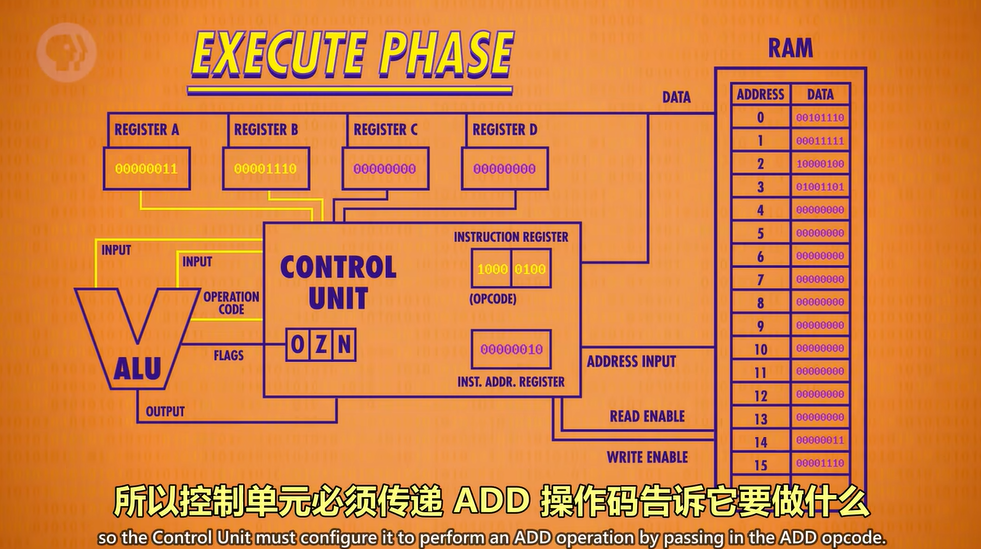
CPU在需要时可以调用ALU
时钟
负责管理 CPU 运行的节奏,以精确地间隔,触发电信号,控制单元用这个信号,推动 CPU 的内部操作。
时钟速度(Clock Speed):CPU 执行“取指令→解码→执行”中每一步的速度叫做“时钟速度”,单位赫兹Hz,表示频率。
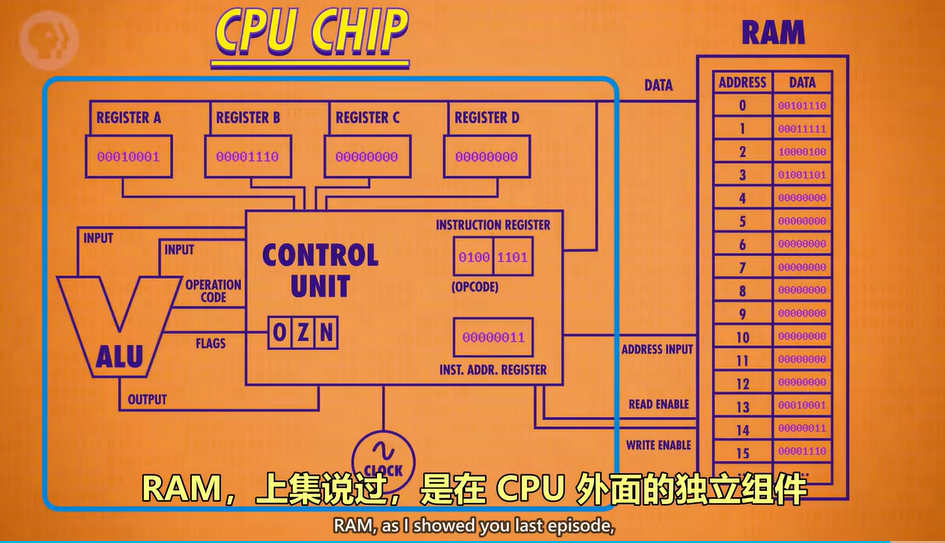
完整CPU的组成:ALU,control unit,clock
RAM并不是CPU的一部分。
参考:
【计算机科学速成课】[40集全/精校] - Crash Course Computer Science


 浙公网安备 33010602011771号
浙公网安备 33010602011771号