聊聊GIS中的坐标系|再版 详细定义、计算及高程系统

本篇讲坐标系统的详细定义，有关坐标系的变换公式，以及简单说说高程坐标系统。

本文约6000字，阅读时间建议45分钟。硬内容比较多，如有疏漏错误请指出，建议有兴趣的朋友进一步阅读。

作者：博客园/B站/知乎/csdn/小专栏 @秋意正寒

版权：转载请告知，并在转载文上附上转载声明与原文链接（https://www.cnblogs.com/onsummer/p/12082454.html）。

目录

1. 地理坐标系统定义

2. 投影坐标系统定义

3. 高程系统

4. 坐标系统转换

1. 地理坐标系统定义

1.1. 人类对地球形状的描述

人类发现地球是个“赤道稍胖”的椭球后，就打算用一些数学或者物理的手段描述地球的形状。

早期，是用一个叫“大地水准面”的概念描述地球的，这个概念的说法是，地球海水静止后，海水面的形状就是地球的形状（陆地部分则想象海水穿过）。

后来，又提出了“似大地水准面”这一概念，它用的就不是海水面了，而是每个地方的重力线的顶点构成的面。

最后，为了便于数学计算，采用“椭球面”这一数学概念来描述地球形状。

在大地测量学中，“大地水准面”、“似大地水准面”所对应的“正高”、“正常高”是必须熟背于心的，但是在GIS中，本篇只讨论最后一个椭球面。

1.2. 旋转椭球面方程

根据解析立体几何，一个旋转椭球面的方程为：

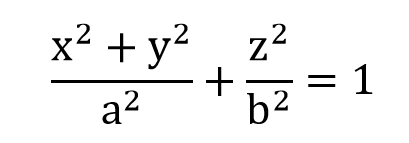
它是个什么玩意儿呢？它是：

一个椭圆，这个椭圆以短轴为z轴，椭圆心为原点，然后绕z轴旋转而成的曲面。

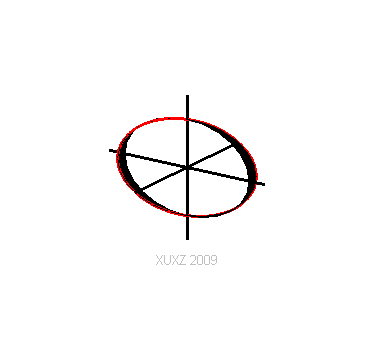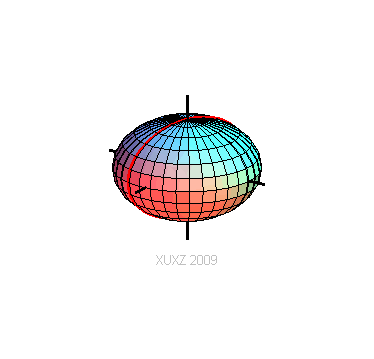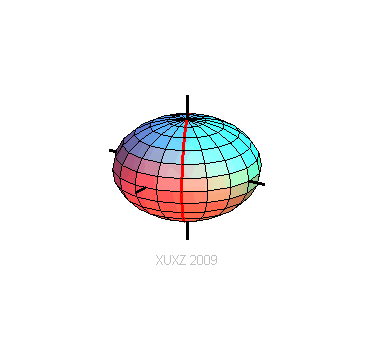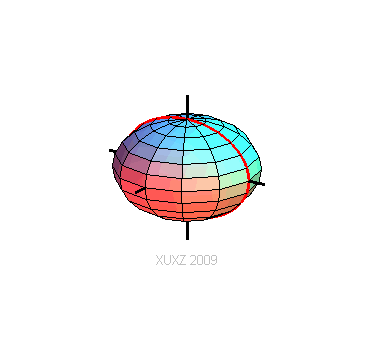
(网络图片, http://xuxzmail.blog.163.com/blog/static/251319162009618102642971/)

用平行于xOy平面的面切这个椭球面，相交的形状是一个圆。

1.3. 球面坐标系与经纬度

根据解析立体几何，常用三种三维空间坐标系，笛卡尔空间直角坐标系、球面坐标系、柱面坐标系。

本节回答为什么三维的经纬度只有两个分量的问题。

球面坐标系的定义是怎么样的呢？

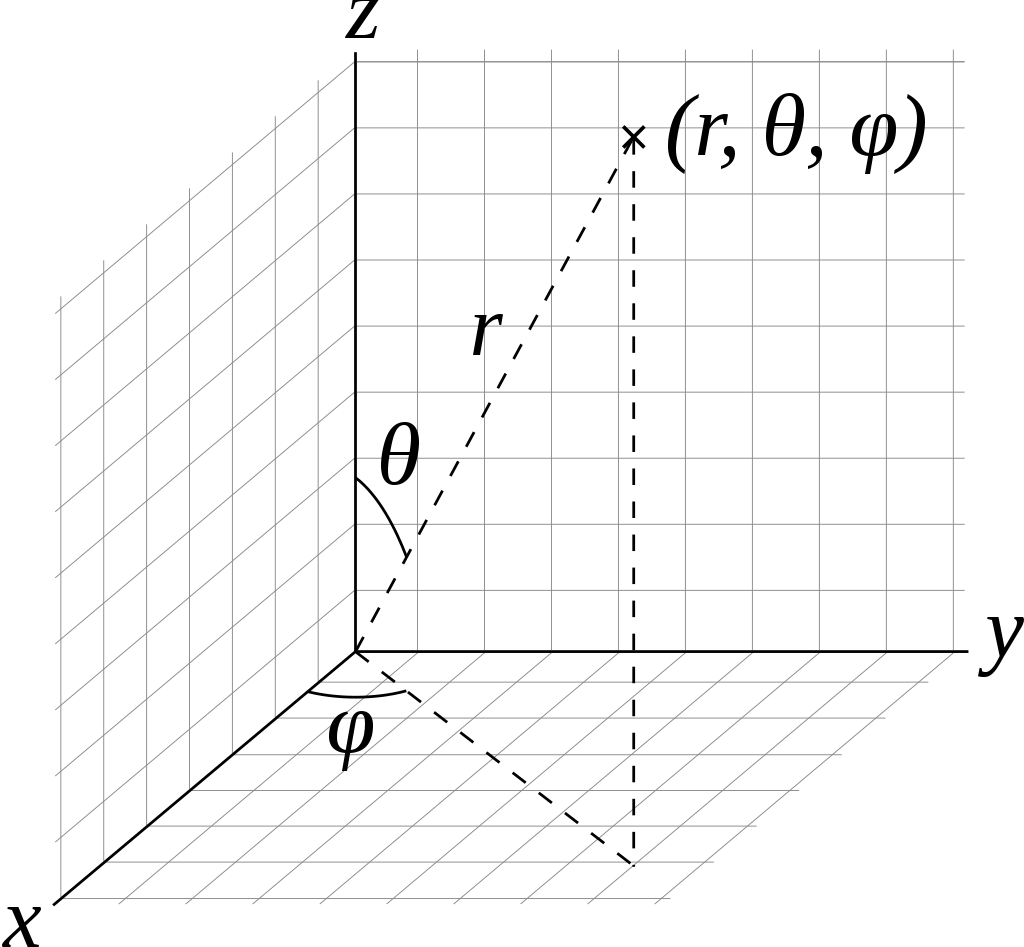
球面坐标是三维坐标，自然有三个分量：r、θ、φ

r表示该点到原点的距离；θ表示该点与原点连线和z轴的夹角；φ表示该点与原点连线在xOy平面的投影和x轴的夹角。

那么，经纬度呢？

我们假想x轴是赤道面上这么一根半径所在的直线：这根半径线段与0度经线相交，也即：

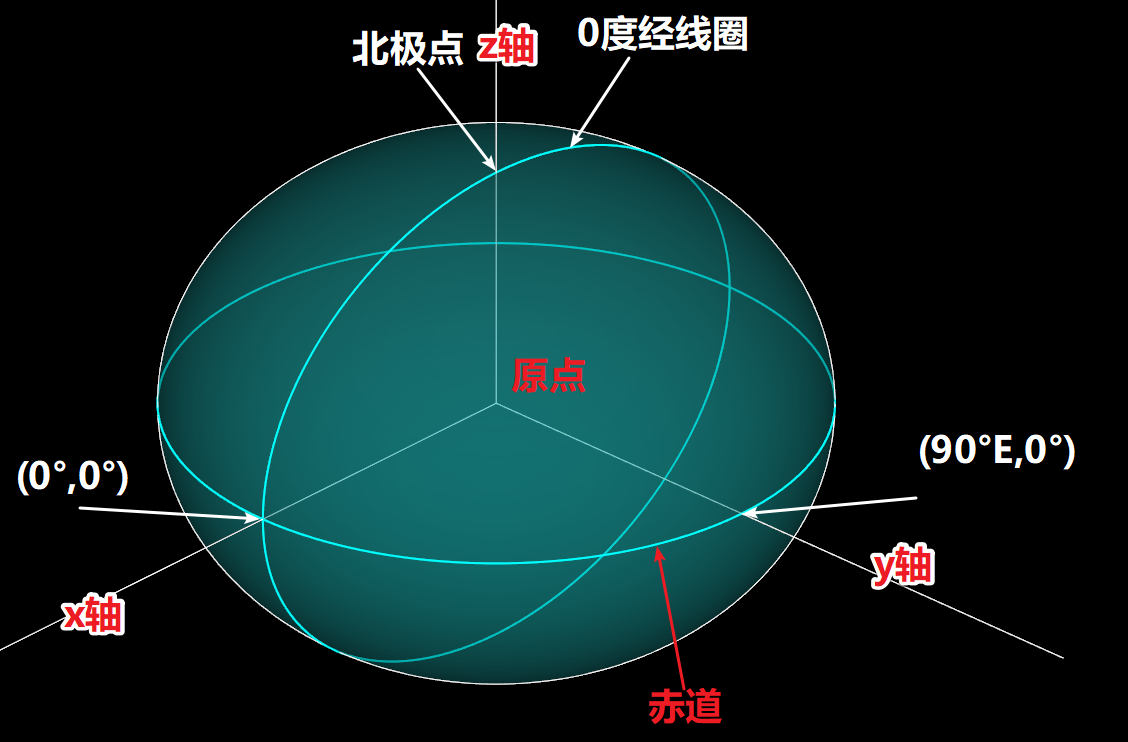
同理，y轴、z轴也有类似的定义。

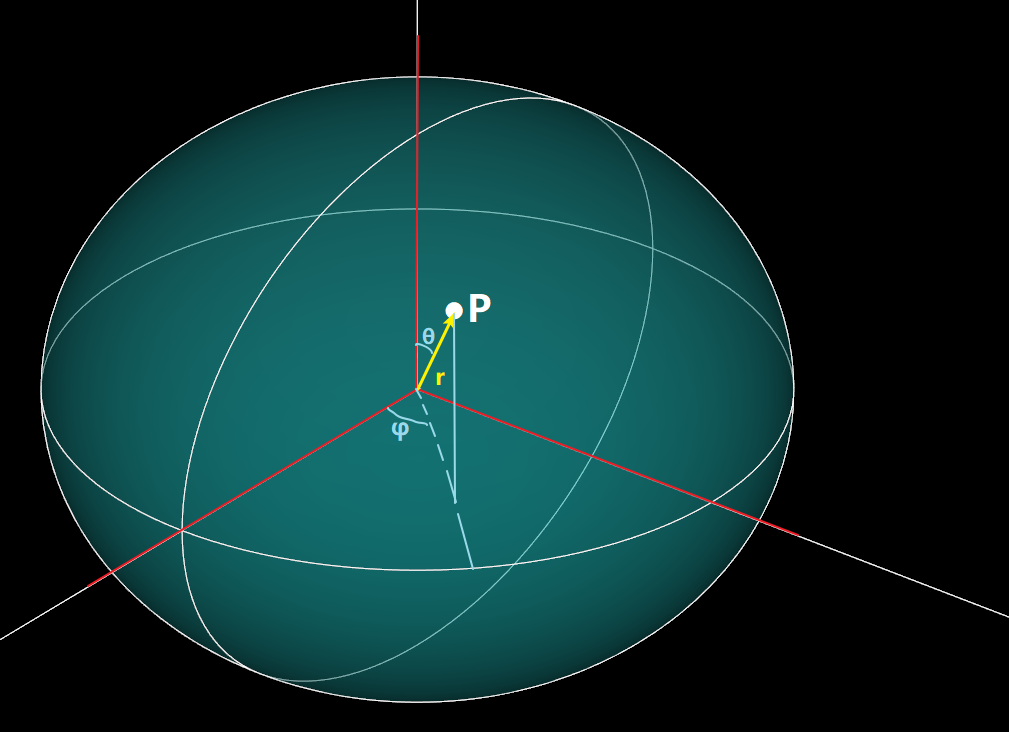
但是，点P（经度，纬度，第三个分量）究竟是什么呢？

其实，经度就是φ，纬度就是θ。

“经度(φ)就是椭球上的点与原点连线这一线段，在赤道平面（xOy平面）上投影与x轴的夹角”——只不过加了东经和西经，并不是0到360°。

“纬度就是椭球上的点与原点连线这一线段，与z轴的夹角的余角。”——赤道上的点与原点连线和z轴的夹角是90度，但是纬度是0度，所以是余角的关系。

所以，第三个分量就十分明确了：r，表示点到原点（椭球心）的距离。但是，为什么平时只用经纬度呢？

那是因为这个r非常大，通常我们谈高度只谈海拔高度，并不谈到地心的距离，所以这个r是被忽略的，这就解释了明明是三维坐标，却只有经纬度两个分量。

如果文字啃得太生硬，可以看下图：

1.4. 椭球与地理坐标系统

根据1.2，得知椭球面方程有两个参数a和b。

根据1.1，得知地球的形状是椭球体，表面是椭球面。

所以，描述地球通常只需要这两个参数即可，我们下一个定义：

定义a为赤道半径，即椭球的长半轴长；

定义b为极半径，即椭球的短半轴长。

赤道半径为地心（椭球心）到赤道任意一点的距离，极半径为地心（椭球心）到任意一个极点的距离。

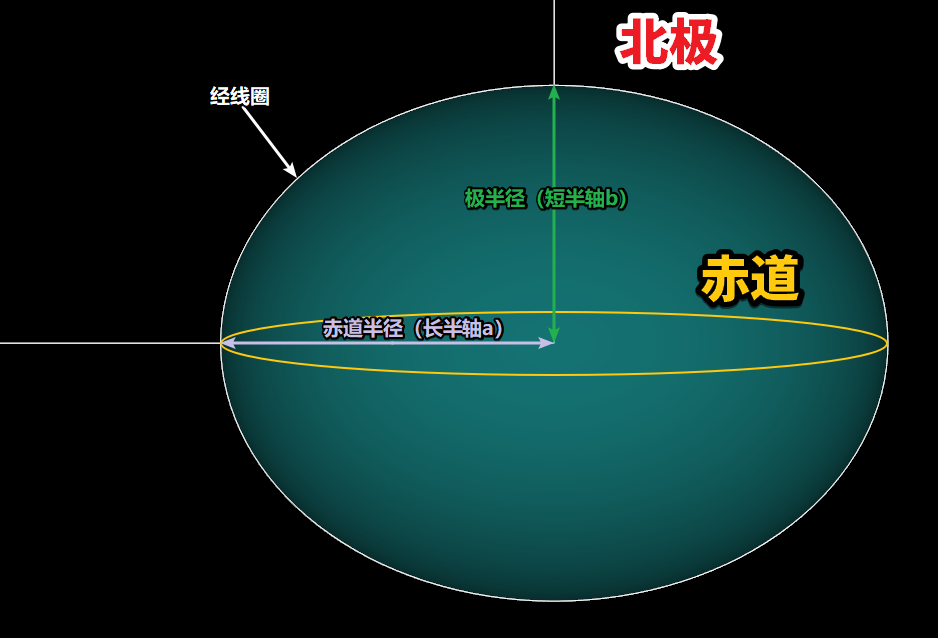
有这两个参数后，还可以延伸出扁率和偏心率这两个概念。扁率有1个，偏心率则有两个。公式定义如下：

 

 

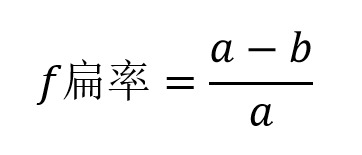
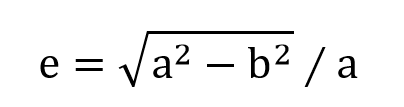
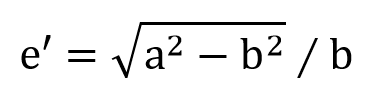
e和e'分别是第一偏心率和第二偏心率。

有了椭球，我们就有了地球的形状。实际上，地理坐标系统（GCS）的定义绝大部分就是由椭球体这两个参数定义的，那么地理坐标系统又是如何定义的呢？

给个公式吧：

GCS = f（椭球体）

f是椭球体的球心对于地球实际中心的偏移。为什么要做偏移？见下节讲解。

1.5. 参心地理坐标系统与地心地理坐标系统

根据1.4，我们知道地理坐标系统是定义在一个数学椭球面上的，具体方程已经给出。

但是还有一个小问题：偏移。

虽然椭球面方程“决定”了地球的形状，但是原点的位置却没有指定。按理说，是统一使用地心才对的，还是处于“懒”，为了方便计算，会直接使用椭球的球心当原点。

事实上，如果地心≠椭球心，椭球面就会比较靠近某个地区，这当然是认为的，这种“靠近”就便于某个国家或地区的计算，因为一旦靠近，很多地方的位置偏差就很小。

我们说，

地心地理坐标系统：椭球的球心=地球的质心

参心地理坐标系统：椭球的球心≠地球的质心

当今为了全球计量需要，有两个我们熟知的地心地理坐标系：WGS84和CGCS2000。

也就是说，北京54和西安80实际上是两个参心坐标系，它们的椭球体分别是克拉索夫斯基1940椭球体和IUGG1975椭球体。

1.6. WKT举例

还是老话，WKT的文章太多了，不再赘述，只摘取一些比较简单的属性讲解。

①WGS84

GEOGCS["WGS 84",
    DATUM["WGS_1984",
        SPHEROID["WGS 84",6378137,298.257223563,
            AUTHORITY["EPSG","7030"]],
        AUTHORITY["EPSG","6326"]],
    PRIMEM["Greenwich",0,
        AUTHORITY["EPSG","8901"]],
    UNIT["degree",0.0174532925199433,
        AUTHORITY["EPSG","9122"]],
    AUTHORITY["EPSG","4326"]]

GEOGCS定义了一个地理坐标系统，内部第一个属性是字符串"WGS 84"是这个地理坐标系的名字。

然后，这个地理坐标系统有基准面"DATUM"，基准面下的"SPHEROID"是椭球体的意思，椭球体下的第二个、第三个属性是长半轴长和扁率的倒数。

最后AUTHORITY属性是这个地理坐标系的WKID信息，是4326.

②CGCS2000

GEOGCS["China Geodetic Coordinate System 2000",
    DATUM["China_2000",
        SPHEROID["CGCS2000",6378137,298.257222101,
            AUTHORITY["EPSG","1024"]],
        AUTHORITY["EPSG","1043"]],
    PRIMEM["Greenwich",0,
        AUTHORITY["EPSG","8901"]],
    UNIT["degree",0.0174532925199433,
        AUTHORITY["EPSG","9122"]],
    AUTHORITY["EPSG","4490"]]

和WGS84类似，不讲了。

1.7. 常见地理坐标系具体信息

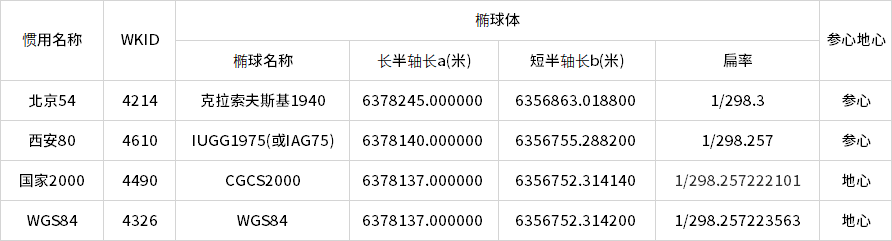
这里不得不说的是，国家2000和WGS84几乎可以兼容，但是得先确定拿到的是真的国家2000的经纬度哦。

轶闻：其实还有一个新北京54坐标系的，WKID是4555，有兴趣的朋友可以查查这个坐标系的历史。

2. 投影坐标系统定义

2.1. 详细定义公式

PCS|x = f1（GCS|经纬度）

PCS|y = f2（GCS|经纬度）

简单解释一下：投影坐标系统的x坐标和y坐标分别由两个计算法则f1和f2计算，需要的参数有经度、纬度、椭球的参数。

2.2. 正算公式与反算公式

根据2.1，查阅资料，以4326做3857投影为例，以及CGCS2000做高斯克吕格投影为例。

不附代码。

① 网络墨卡托投影坐标系统

此处设网络墨卡托的地理坐标系统基于正球体，半径为R，点P的经纬度均为弧度十进制数：

x=R×弧度十进制经度

y=R×ln(tan(π/4 + 弧度十进制纬度/2))

此时，反算公式比较容易推导，不讲了。

② 高斯克吕格基于国家2000投影坐标系统

• 预备参数：椭球长半轴a；椭球扁率f；椭球短半轴b；椭球的第一第二偏心率e1、e2。

• 必备参数：经度J，纬度W

=====分割线=====

第一步，计算辅助量R、t、η、p、X、dL

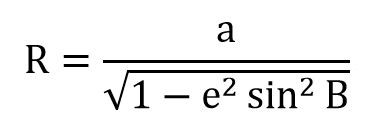• （子午圈（就是所在投影带的中央经线圈）半径）

• t=tanB
• 
• p=180*3600/π
• （子午线弧长）
• dL=B-中央经线度数

 第二步，计算辅助常量a0、a2、a4、a6、a8和m0、m2、m4、m6、m8：

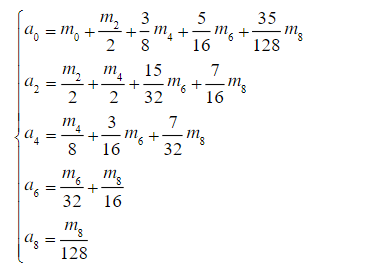
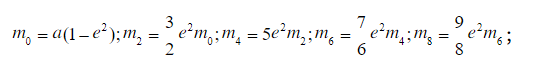  （这里e就是e1）

 第三步，计算xy坐标：

 

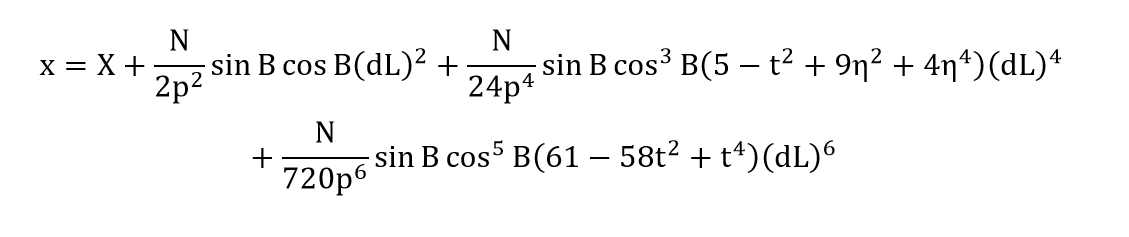
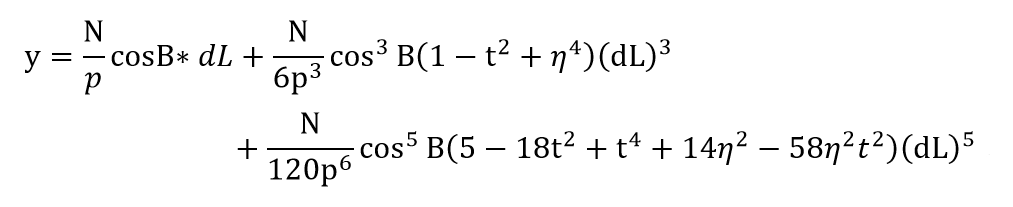
反算公式即从x、y坐标算经纬度坐标。

此处不做展开，有兴趣的朋友可以查阅文末的参考文档。 

2.3. 投影带问题

①换带操作

在arcgis中操作，其实只需要重投影即可。

一种方法是使用“投影”工具，将投影坐标系统的数据重新投影到它原本的地理坐标系统上，然后再用一次“投影”工具将地理坐标系统的数据再次投影到目标坐标系统上，完成换带。

另一种方法是直接用“投影”工具，将投影坐标系统的数据投影到目标PCS上即可。

具体操作见第4节。

②高斯克吕格投影坐标的判断

附一个坐标判断例子：

（41569821,4590855），已知在中国境内，已知地理坐标是国家2000.

横坐标是八位数，那么前两位一定是带号，41度带，那么就不可能是六度带，结果是三度带的高斯克吕格投影坐标系统，WKID是4529.

2.4. WKT举例

①网络墨卡托

PROJCS["WGS 84 / Pseudo-Mercator",
    GEOGCS["WGS 84",
        DATUM["WGS_1984",
            SPHEROID["WGS 84",6378137,298.257223563,
                AUTHORITY["EPSG","7030"]],
            AUTHORITY["EPSG","6326"]],
        PRIMEM["Greenwich",0,
            AUTHORITY["EPSG","8901"]],
        UNIT["degree",0.0174532925199433,
            AUTHORITY["EPSG","9122"]],
        AUTHORITY["EPSG","4326"]],
    PROJECTION["Mercator_1SP"],
    PARAMETER["central_meridian",0],
    PARAMETER["scale_factor",1],
    PARAMETER["false_easting",0],
    PARAMETER["false_northing",0],
    UNIT["metre",1,
        AUTHORITY["EPSG","9001"]],
    AXIS["X",EAST],
    AXIS["Y",NORTH],
    EXTENSION["PROJ4","+proj=merc +a=6378137 +b=6378137 +lat_ts=0.0 +lon_0=0.0 +x_0=0.0 +y_0=0 +k=1.0 +units=m +nadgrids=@null +wktext  +no_defs"],
    AUTHORITY["EPSG","3857"]]

• 最外层是PROJCS，即投影坐标系统。
• 第一个属性"WGS 84 / Pseudo-Mercator"是这个坐标系的名称。
• 第二个属性GEOCS是这个投影坐标系统的地理坐标系统，详见上文。
• 第三个属性PROJCTION是投影方法"Mercator_1SP"。
• 第四~七个属性是其他属性，顺序下来是中央经线经度、比例因子、假东、假北。
• 第八个属性是单，第九个、第十个属性分别指示X和Y的方向是东和北。
• 第11个属性是此投影坐标系统在PROJ4中的定义。
• 第12个属性是此投影坐标系统在EPSG中的WKID。

②国家2000的高斯投影

以WKID=4547为例：

PROJCS["CGCS2000 / 3-degree Gauss-Kruger CM 114E",
    GEOGCS["China Geodetic Coordinate System 2000",
        DATUM["China_2000",
            SPHEROID["CGCS2000",6378137,298.257222101,
                AUTHORITY["EPSG","1024"]],
            AUTHORITY["EPSG","1043"]],
        PRIMEM["Greenwich",0,
            AUTHORITY["EPSG","8901"]],
        UNIT["degree",0.0174532925199433,
            AUTHORITY["EPSG","9122"]],
        AUTHORITY["EPSG","4490"]],
    PROJECTION["Transverse_Mercator"],
    PARAMETER["latitude_of_origin",0],
    PARAMETER["central_meridian",114],
    PARAMETER["scale_factor",1],
    PARAMETER["false_easting",500000],
    PARAMETER["false_northing",0],
    UNIT["metre",1,
        AUTHORITY["EPSG","9001"]],
    AUTHORITY["EPSG","4547"]]

• 最外层是PROJCS，即投影坐标系统。
• 第一个属性"CGCS2000 / 3-degree Gauss-Kruger CM 114E"是这个坐标系的名称。
• 第二个属性GEOCS是这个投影坐标系统的地理坐标系统，详见上文。
• 第三个属性PROJCTION是投影方法"Transverse_Mercator"，横轴墨卡托的意思。
• 第四~八个属性是其他属性，顺序下来是起始经线经度、中央经线经度、比例因子、假东、假北。
• 第九个属性是单位。
• 第十个属性是此投影坐标系统在EPSG中的WKID。

假东是什么意思？因为如果用赤道和中央经线的交点作为原点，投影得到的原始坐标会有负值。

我们记原始坐标为P，则给y坐标（经度方向）加500km后的P'就不会是负值了。

在P'的y坐标值（经线方向）加上带号，例如上图中的红色数字20，就成了带带投影带的坐标。

x方向的坐标一般不变，除非在地方坐标系中有需要，则设置假北（False North）。

2.5. 投影坐标系统的xy和ArcGIS的xy

在测量学的规定中，投影坐标系统上，x方向是指南北方向，y方向则是东西方向；

而在ArcGIS中，x方向则是东西方向，y方向是南北方向，正好颠倒。

所以，获取一份投影坐标系统的数据时，如果是正统的测量数据，那么y值应该在导入ArcGIS时被用于x，x值则用于y。

ps：我一直觉得，x和y只是一个记号，但是人就是那么喜欢用，换ab也可以，用uv也可以，切记：只是个符号，不要把xy的方向绝对化。

3. 高程系统

3.1. 1985国家高程基准

由1.3小节，我们知道球面坐标的第三个参数，点到椭球心（原点）的距离一般来说没什么用，我们听到更多的是“海拔高度”。

什么是海拔高度？珠穆朗玛峰海拔高度8844.43米，这个就是海拔高度。

那这个海拔高度的起点，也就是0米，是以那个地方的地面作为依据的呢？

答案就是，我国的“1985国家高程基准”，它的基准点位于青岛市某个地方，基准点高度为72.260m。

这个72.26m是什么意思呢？就是指，这个地方作为我国所有高程测量的起始值，别处测量的高度再加上72.26m即海拔高度。

3.2. GPS的高度——大地高度vs海拔高度

我们在文章开头1.1小节处，提及了正高和正常高两个概念，我们不引入太多测量学里的定义，但是，我国的高程系统一律是使用“正常高”的。

我们定义一个高度：大地高度H

大地高度是什么意思呢？大地高度就是点到椭球面的距离（沿着法线）。与1.3节定义的到椭球心的距离r相比，少了好长一截（暂停5分钟，读者可以想象一下）。

由卫星测得的高度就是大地高度。

那么大地高度H和我们说的海拔有什么关系呢？我们说我国高程测量是用“正常高”这个方法的，即重力等位面。

而我国的海拔高度又是基于正常高的，记作H'，那么H和H'的关系是：

H=H'+a

这里的a代表的意义是，“正常高”为零时的那个面距离椭球面的高度。回忆一下1.1节的内容，这个面是什么？

“正常高”的面是重力等位面，也即似大地水准面。

我们画个图表示表示：

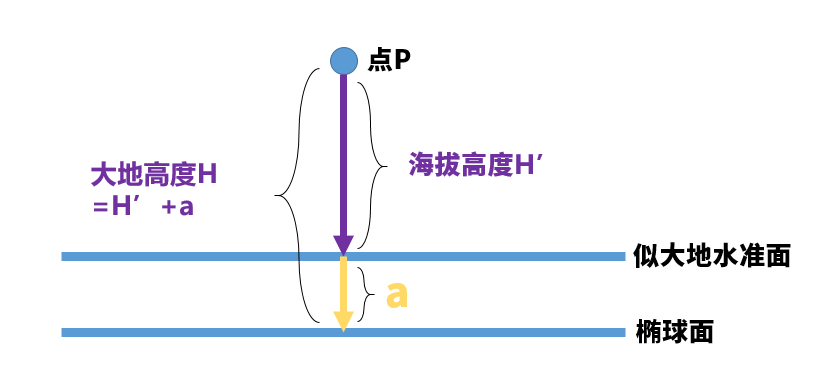
当然，大地水准面也有类似的图：

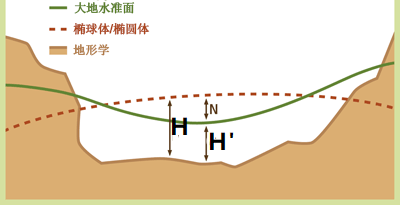
此时大地高度H=H'+N，N即大地水准面到椭球面的距离，H'即正高（实际点到大地水准面的距离）。

plus：美国GPS的经纬度定位精度是不错的，但是高程的测量就比较差。

4. 坐标系统转换

4.1. n参数（n=3，4，7）与地理转换

①n参数

一个坐标系统挪到另一个坐标系统，有哪些情况呢？

最简单的是平移原点，只需要给出三个方向的平移量dx、dy、dz，此时，称之为三参数转换；

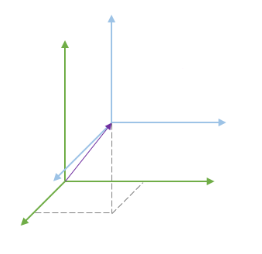
复杂的还可以加上4个量：三个方向的旋转角度α、β、γ+统一的缩放比例k，称之为七参数转换；

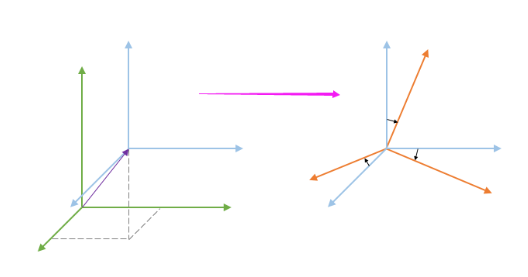
另外，如果是平面上二维坐标系的转换，可以使用两个平移量dx、dy，一个旋转角度α，一个缩放比例k来完成。

举个例子，在珠海既有基于北京54的投影坐标系统又有珠海的自己的地方投影坐标，在这两种坐标之间转换就用到四参数。四参数的获取需要有两个公共已知点。

如果区域范围不大，最远点间的距离不大于 30Km（ 经验值 ） ，这可以用三参数或者四参数。

坐标系统转换的实质就是地理坐标系统的转换，也即椭球体的转换。

当然，在书本上，会有投影坐标系统直接转换而不经过地理坐标系统的算法（《地理信息系统概论》黄杏元第三版），但是那个比较难。

②地理转换

在ArcGIS中，允许用户自定义七参数或三参数来进行不同椭球体（不同地理坐标系）的转换，当然，这些所谓的七参数和三参数的获取，至少在国内的转换中，是保密的，需要到有关部门购买相同位置的三个点的两个不同坐标系下的坐标，然后自己计算得到七参数。

有关这些参数的计算，参考更丰富的测量专业的书籍或者博客。

假设已经获取了七参数/三参数，那么可以在ArcMap中，使用“创建自定义地理(坐标)转换”工具为这些参数定义一个“地理转换”：

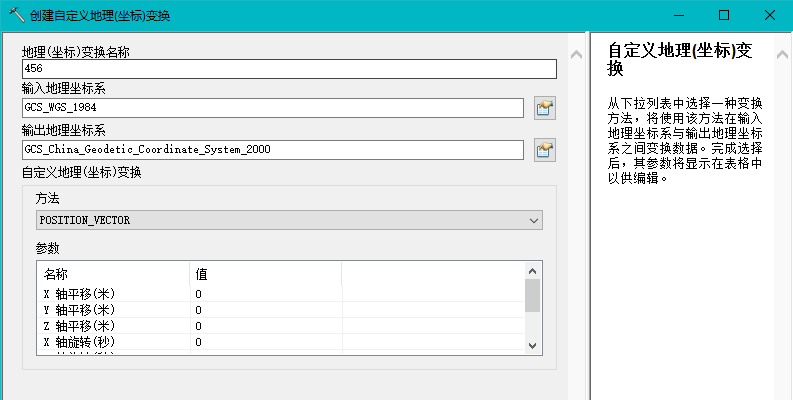
方法参数有很多，选一个需要的即可，不懂是啥的可以百度一下（我也没用过，大家可以边搜边试）。

4.2. ArcGIS中重投影操作

使用“地理转换”工具和“投影”/“投影栅格”工具。以下以矢量数据为例，使用“投影工具”。

①PCS1转PCS2（不同GCS）（使用投影工具）

跨不同地理坐标系统的转换，需要使用4.1提及的自定义地理(坐标)转换工具创建地理转换。

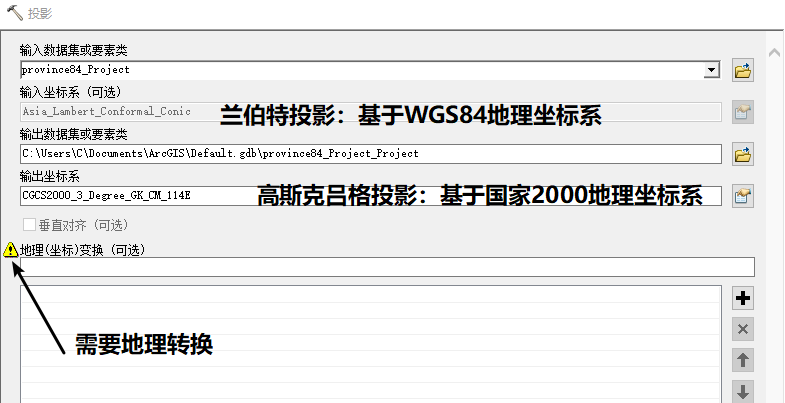
②PCS1转PCS2（相同GCS）（使用投影工具）

③PCS1回算PCS1.GCS（使用投影工具）

④GCS1转GCS2

两个不同地理坐标系的数据进行坐标系转换，需要使用4.1提及的自定义地理(坐标)转换工具创建地理转换：

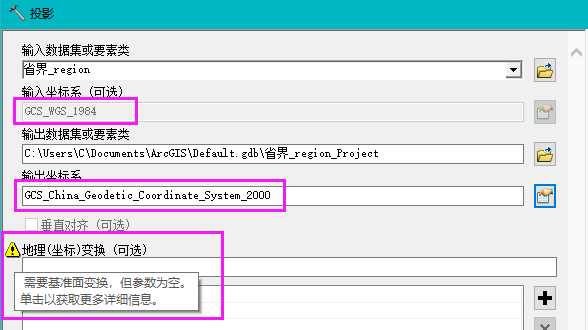
此处为WGS84到国家2000，椭球不同，必须使用地理转换。

我们发现，需要地理转换的操作，通常就意味着跨地理坐标系统转换；

反过来说，跨地理坐标系统的转换就需要一个地理转换定义，也即n参数。

4.3. 前端转换计算之turf.js

turf.js只支持3857和4326的互转。

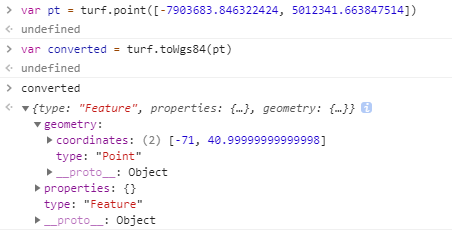
①使用turf.toWgs84()转换网络墨卡托的xy坐标到经纬度

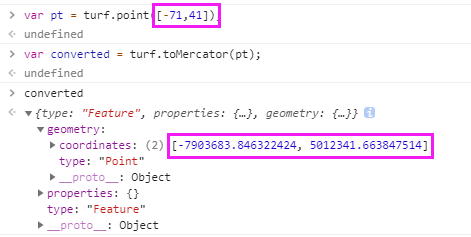
②使用turf.toMercator()转换经纬度到xy网络墨卡托坐标

4.4. 前端转换计算之openlayers(6.x)

主要功能都在ol/proj模块下，另外在自定义坐标系和转换时会用到第三方库proj4.js，但本文非开发类的博客，不细展开。

①ol/proj.fromLonLat(coordinate, opt_projection)方法

fromLonLat方法将经纬度coordinate转换到目标坐标系opt_projection下，opt_projection默认值是"EPSG:3857"，是“ProjectionLike”类型的参数。

对应方法是ol/proj.toLonLat()。

②ol/proj.get(string)

获取坐标系信息，string是"EPSG:3857"的字符串，必须大写EPSG。这个字符串在openlayer6中叫做“ProjectionLike”类型。

返回一个ol/proj/Projection类型的对象

③ol/proj.addCoordinateTransforms(source, destination, forward, inverse)

添加两个坐标系之间的转换方法，source是待转换坐标系，destination是目标坐标系，二者均以"EPSG:XXXX"的字符串传入。

forward是

④ol/proj.proj4.register(proj4)

让openlayer知道你注册了一个自定义坐标系统。详情请参考proj4.js有关资料。

⑤ol/proj.getTransform(source, destination)

给定待转换坐标系source和目标坐标系destination，返回二者之间的转换方法。

⑥ol/proj.transform(coordinate, source, destination)

将坐标点从source坐标系到destination坐标系转换，source和destination均为"EPSG:xxxx"的字符串（即“ProjectionLike”类型），EPSG四个字母大写。

4.5. 前端转换计算之cesium

cesium只支持4326和3857的互相转换。常用的类有如下几个：

①Cesium.MapProjection类

属性：

ellipsoid。Ellipsoid类型，即椭球。

方法：

project()和unproject()。一个用于将地理坐标转换为投影坐标，一个用于将投影坐标转回地理坐标。详见API。

②Cesium.GeographicProjection(ellipsoid)类

表示地理坐标系统的一个类，使用Ellipsoid类型的参数进行实例化。方法与MapProjection类相同。

默认构造参数是Ellipsoid.WGS84

③Cesium.WebMercatorProjection(ellipsoid)类

表示网络墨卡托投影坐标系统的一个类，使用Ellipsoid类型的参数进行实例化。

默认构造参数是Ellipsoid.WGS84（是不是很奇怪，和上面那个一样）

也拥有project()和unproject()两个方法。详见API。

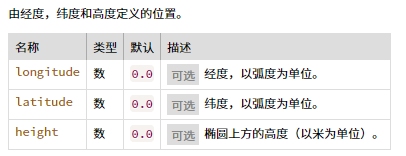
④Cesium.Cartographic(longitude, latitude, height)类

这个类的意思就是一个地理坐标系统下的点，包括经度longitude，纬度latitude，和大地高度height

静态方法：

• Cesium.Cartographic.fromCartesian(Cartesian3对象, ellipsoid, result)：将投影坐标实例Cartesian3转换到地理坐标系统ellipsoid上，通常ellipsoid参数是Ellipsoid.WGS84。
• Cesium.Cartographic.fromDegrees(经度,纬度,大地高度,result)：创建一个地理坐标点
• Cesium.Cartographic.fromRadians()：同上只不过用弧度制
• Cesium.Cartographic.toCartesian()：将地理坐标转换为投影坐标

⑤Cesium.Cartesian3(x, y, z)类

笛卡尔坐标点，即投影坐标点。

该类也提供了类似Cartographic类的转换方法，详情请自行查阅API文档。

4.6. *硬改数据坐标系的定义

在gis软件中为数据重新定义一个坐标系，这有可能出现极大问题。通常不推荐做这种非精确的转换。

曾经在实践中遇到过类似的问题，就是很多情况下，有的人并不在意坐标系有多么精确，甚至有时候，能把数据强硬编辑挪到喜欢的位置上就罢了。

事实上，在精度不高的情况下（例如一个城市，或者一个城市群这么大级别的区域），直接改动数据的坐标系统的定义，而不是经过精确的地理转换、坐标转换计算，有时候在这么大的尺度下可能看不出来什么。

有个特例，WGS84和国家2000坐标系的改动——因为这两个坐标系的的确确很接近。什么？你跟我说硬改还是很大偏差？

那你考虑一下你是否拿到了真的国家2000坐标，而不是什么所谓的GCJ02和BD09。

 

碎碎念

又熬夜了，能在2019年结束前重写完坐标系这三篇博客，也算是对自己的一个承诺的实现了。

我知道在大地测量学专业上有更加精妙的计算，有更为严苛的定义和转换，但是，作为一个GIS从业者，能用上测量学和地图学的坐标系统成果，已经游刃有余了。

我希望我的读者也能明白这点，未来加油。

 

参考文档

[1] 高斯正反算公式：https://wenku.baidu.com/view/5776611cd4d8d15abf234e14.html

[2] 信息工程大学ppt：https://wenku.baidu.com/view/88fb6e0d84868762cbaed50d.html

[3] 扒一扒坐标转换之七参数：http://www.sohu.com/a/318537831_689260

[4] 写给测绘小白，讲解四参数与七参数坐标转换含义及区别：https://rtkhome.com/?p=1210

[5] 布尔莎-沃尔夫转换模型的几何证明：https://wenku.baidu.com/view/11bbf607ba1aa8114431d97f.html