个人感觉质量很不错的一套题，难度适中很适合我这种小白去做。不过由于在下能力有限，本文只会讲我通过的那些题。在难度上AHIK--FG--CB,接下来我会按这个难度顺序讲解。
A 造数
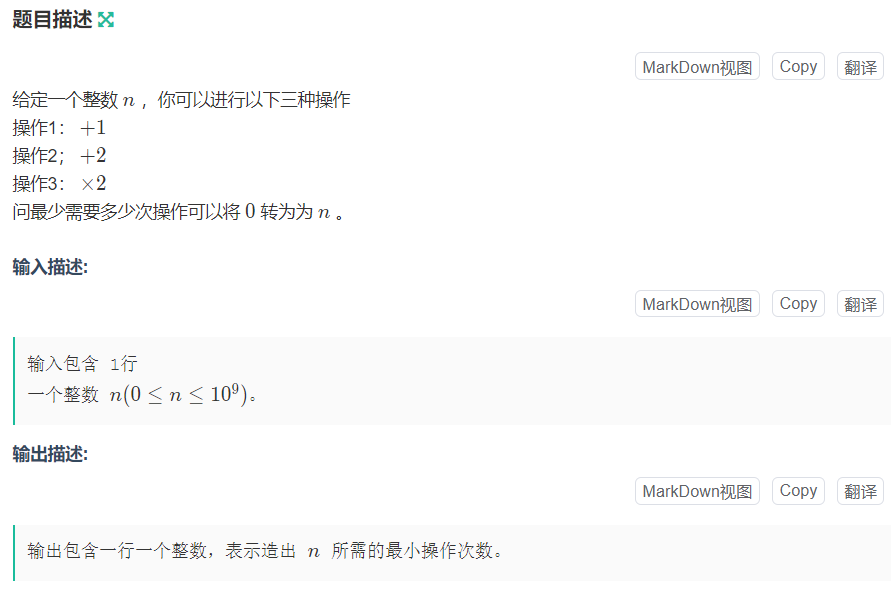
我们模拟一下它从n到0的过程，要让n变小，肯定是在n>2的时候不断向下除以2，我们假设一个数4到9，正着来就是*2再＋1，那么倒过来就是-1再/2。偶数则直接除以2，最后特判一下2的时候直接减就行了。
点击查看代码
signed main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int n,cnt=0;
cin>>n;
while(n>0)
{
cnt++;
if(n==2) n-=2;
if(n%2) n--;
else n/=2;
}
cout<<cnt;
}
H 两难抉择
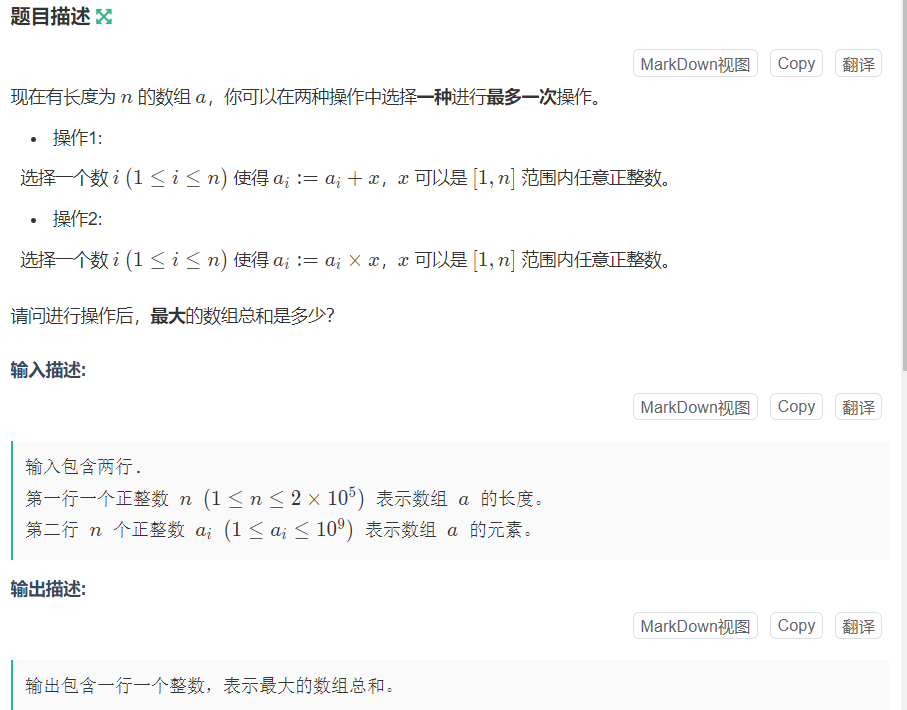
第一个操作肯定选择加n会让总和最大，第二个操作选择最大的数让它×n最大。然后输出这两个的最大值就行了。
点击查看代码
void solve()
{
int sum=0;
cin>>n;
for(int i=1;i<=n;i++){
int x;
cin>>x;
sum+=x;
ve.push_back(x);
}
sort(ve.begin(),ve.end());
int mx=ve[ve.size()-1];
cout<<max(sum-mx+mx*n,sum+n);
}
I 除法移位
需要注意这题的除法不是向下取整，而是1/2=二分之一这样的正常除法。所以对原式就有:S=a1/a2a3...an。就是只有第一位是分子，其它都是分母。那么我们对每个数都有让它作分子也就是移到第一位需要的操作数，遍历一遍找到在允许的操作数内能找到的最大分子即可。
点击查看代码
void solve()
{
cin>>n>>q;
for(int i=1;i<=n;i++)
{
cin>>a[i];
int t=(n-i+1)%n;
ve.push_back({a[i],t});
}
int res=0,id=0;
sort(ve.begin(),ve.end());
for(auto x:ve)
{
int num=x.first,cnt=x.second;
if(cnt<=q)
{
if(num>res)
{
res=num;
id=cnt;
}
else if(num==res)
{
id=min(cnt,id);
}
}
}
cout<<id;
}
K 图上计数(Easy)
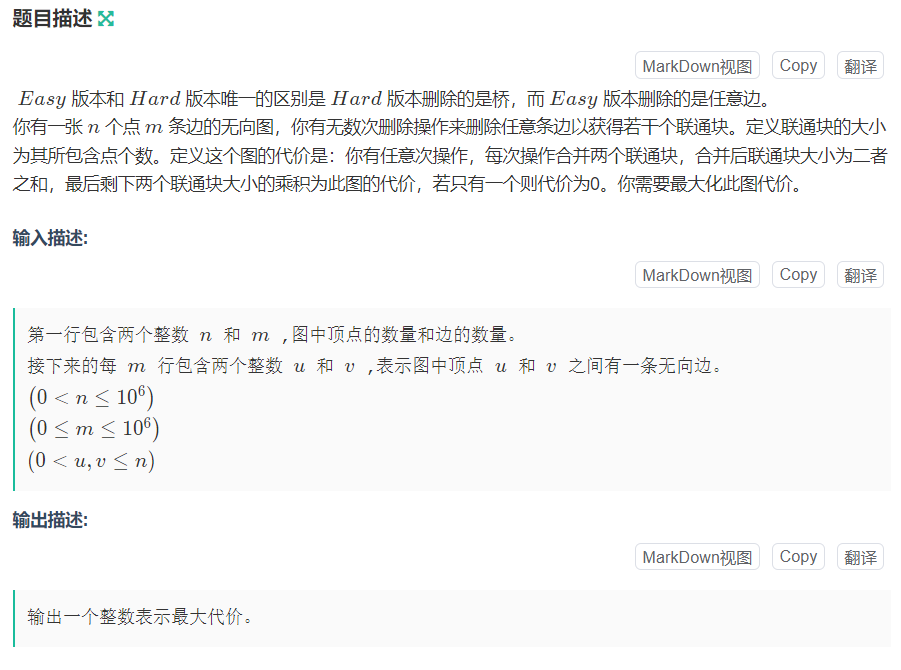
考虑到所有图都可以无限拆分再重组，那么我们把所有图都拆成点数为1的单位图。那么我们就可以得到n个独立的点，这n个点可以随意组装。那么最大代价就是ab,而a+b==n。易得当a,b越接近时S=ab最大。也就是a=n/2,b=n-a。
点击查看代码
void solve()
{
int n;
cin>>n;
cout<<n/2*(n-n/2);
}
F 两难抉择新编
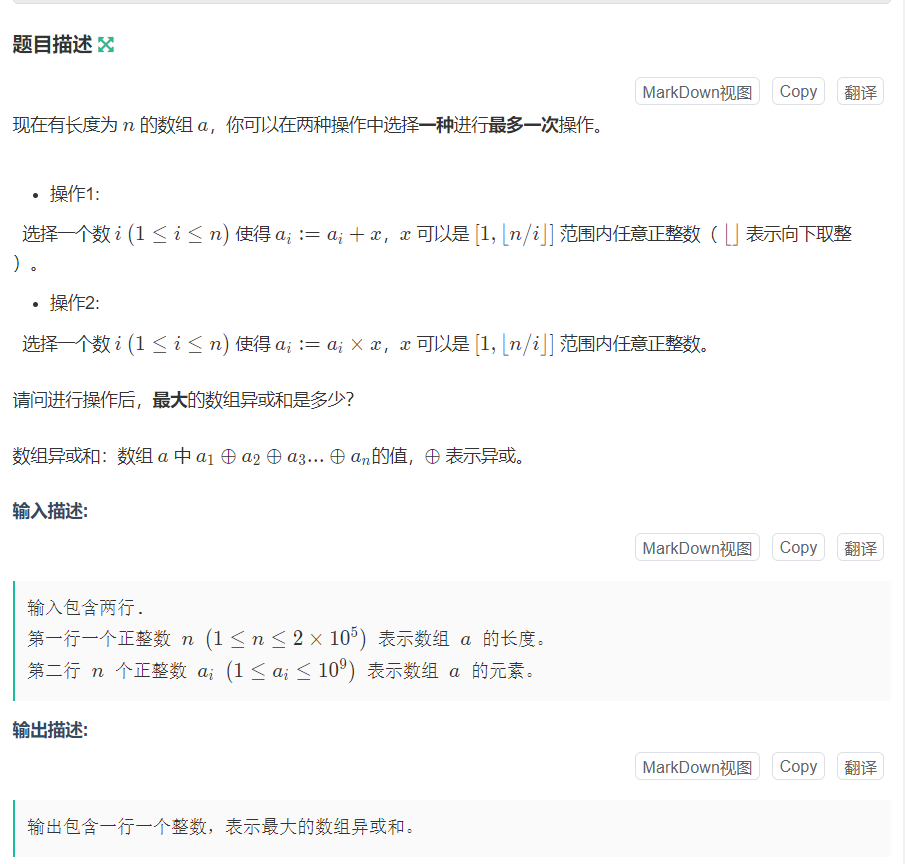
注意到1-n/i是个n/1+n/2+n/3+...+n/n的调和级数。所以直接暴力遍历即可。这里用到了异或的运算法则。设sum = a ^ b,那么sum ^ a = b。所以存入数组时作sum为异或和，暴力时异或掉a[i]，然后在异或a[i]*k即可。
点击查看代码
void solve()
{
int sum=0;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
sum^=a[i];
}
int ans1=sum,ans2=sum;
for(int i=1;i<=n;i++)
{
int mx=n/i;
for(int j=1;j<=mx;j++)
{
int k=sum^a[i];
ans1=max(ans1,k^(a[i]+j));
}
}
for(int i=1;i<=n;i++)
{
int mx=n/i;
for(int j=1;j<=mx;j++)
{
int k=sum^a[i];
ans2=max(ans2,k^(a[i]*j));
}
}
cout<<max(ans1,ans2);
}
G 旅途的终点
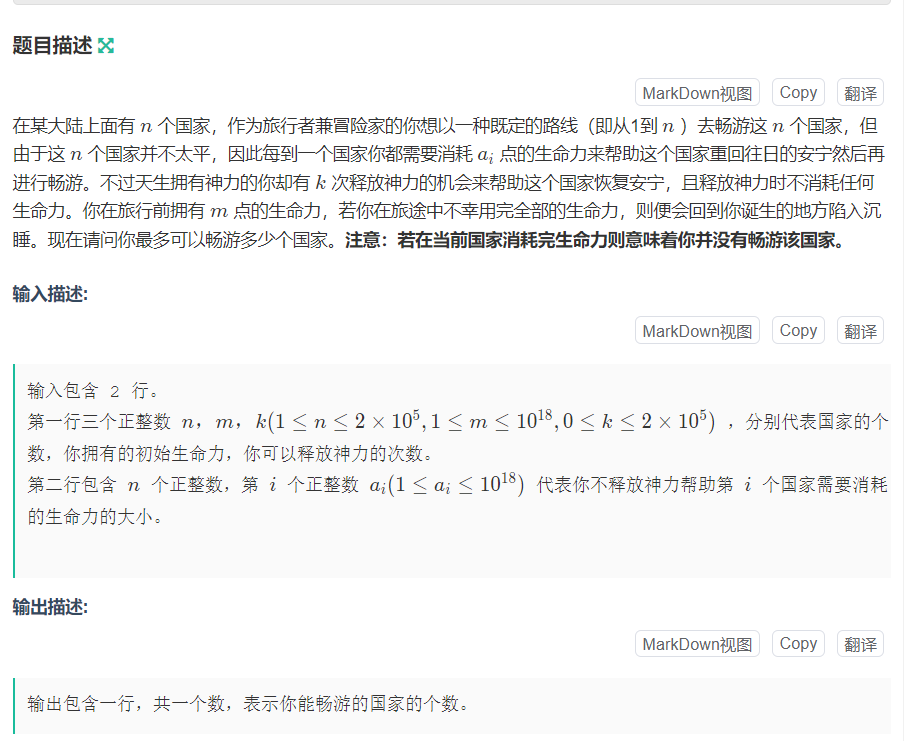
这道题贪心或者二分答案都可以。以下给出两种做法，先是贪心，就用类似反悔贪心的思想。先把前K个数当成使用了能力的位置。然后在k+1开始，开一个小根堆，每次先存入当前数，这样每次弹出的肯定是消耗生命最少的点。将伤害累加起来，如果此时你的生命不够负担这些伤害了就结束，否则继续往前走。
点击查看代码
void solve()
{
priority_queue<int,vector<int>,greater<int>>q;
cin>>n>>m>>k;
for(int i=1;i<=n;i++) cin>>a[i];
if(k>=n) {
cout<<n;
return ;
}
for(int i=1;i<=k;i++) q.push(a[i]);
int sum=0;
for(int i=k+1;i<=n;i++)
{
q.push(a[i]);
sum+=q.top();
q.pop();
if(sum>=m)
{
cout<<i-1;
return ;
}
}
cout<<n;
}
二分的思路就是二分答案，因为你肯定越往前走掉的血越多，那么答案是具有单调性的。check过程就是对于你选择的前x个数字，大的用技能消掉，剩下的扣血，如果血没扣完就说明这个答案成立，否则不行。
点击查看代码
bool check(int x)
{
vector<int> ve;
for(int i=1;i<=x;i++) ve.push_back(a[i]);
sort(ve.begin(),ve.end(),greater<int>());
int sum=0;
for(int i=k;i<x;i++) {
sum+=ve[i];
if(sum>=m) return 0;
}
return 1;
}
void solve()
{
cin>>n>>m>>k;
for(int i=1;i<=n;i++) cin>>a[i];
int l=0,r=n;
while(l<r)
{
int mid=l+r+1>>1;
if(check(mid)) l=mid;
else r=mid-1;
}
cout<<l;
}
C 有大家喜欢的零食吗
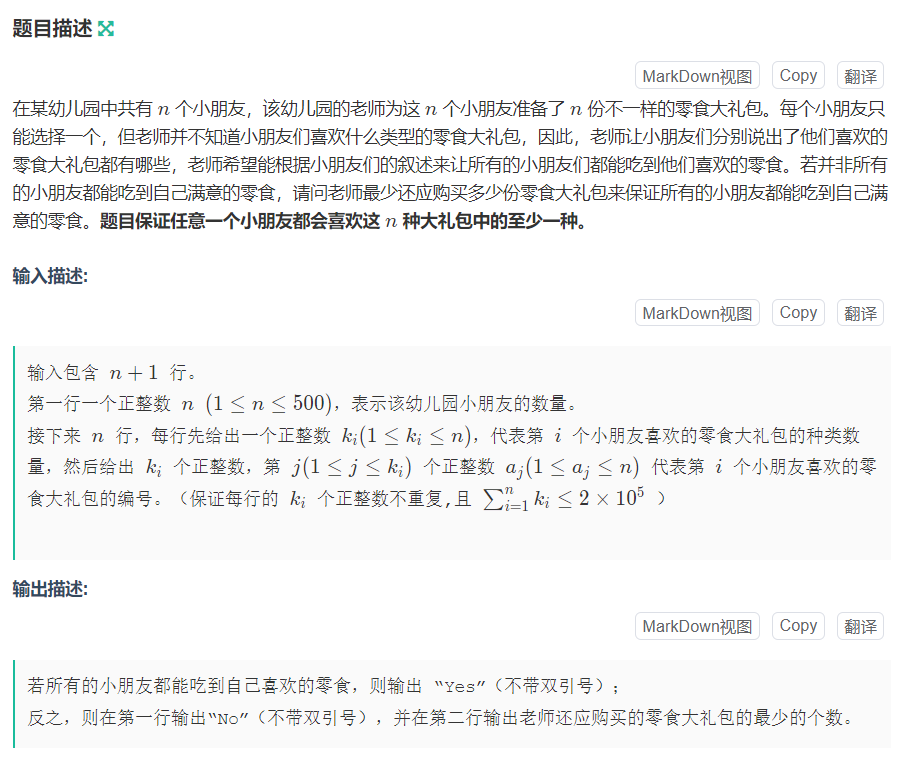
这个其实没啥好说的，就是二分图最大匹配的板子题。大家若是不知道这个算法可以去学一下。就是小孩去匹配零食，每个人都有几种自己喜欢的，你得怎么分才能让更多的小孩拿到自己喜欢的零食。套个板子就行。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 521;
int nv[N],n;
bool vis[N];
vector<int> h[N];
bool dfs(int u)
{
for(auto v:h[u])
{
if(vis[v]) continue;
vis[v]=1;
if(!nv[v]||dfs(nv[v])) {
nv[v]=u;
return 1;
}
}
return 0;
}
signed main()
{
cin>>n;
for(int i=1;i<=n;i++){
int s;
cin>>s;
while(s--)
{
int v;
cin>>v;
h[i].push_back(v);
}
}
int ans=0;
for(int i=1;i<=n;i++)
{
memset(vis,0,sizeof vis);
if(dfs(i)) ans++;
}
if(ans==n) cout<<"Yes";
else cout<<"No"<<endl<<n-ans;
}
B 爱探险的朵拉
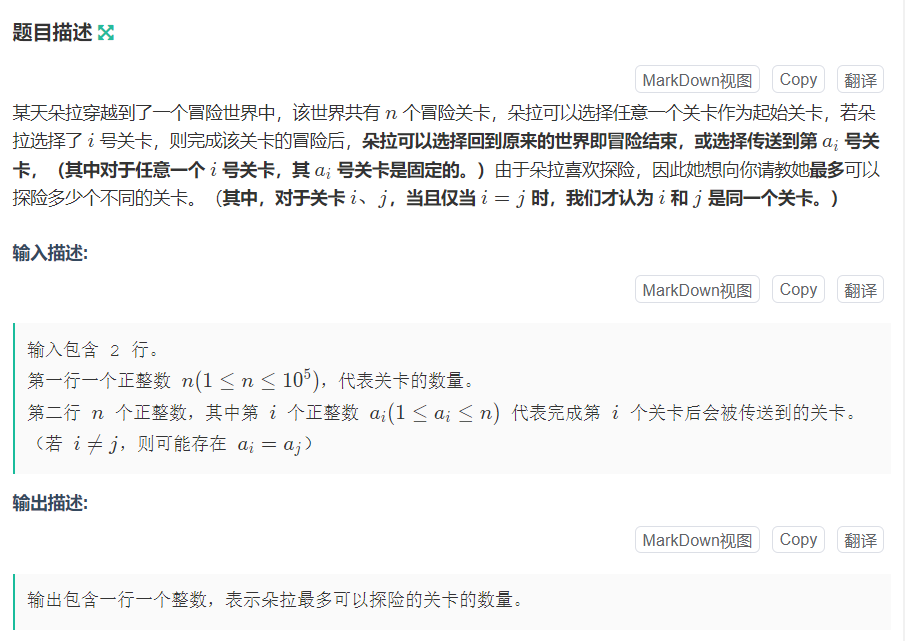
感觉挺不错的一个题。就是从i可以走到a[i]，问你怎么走走的点最多。我们可以把作一条从i到a[i]的有向边。那么问题就转换成了从一个图上，找一条最长子链。因为i是从1到n没有重复的，也就是说对于任意一个点，它的出度是1。如果该图没有环只有一个子链我们很好解决，就是记忆化搜索一下找到最长子链即可。但如果形成环的话，那么它就是一个内向基环树，普通的记忆化搜索对于1->2->3->1搜出的长度是1,2,3但实际上它们每个大小都是3。那么我们可以先用SCC缩点，将环缩成一个点，那个点的大小就是这个环里点的个数。然后再记忆化搜索即可。或者是找到每个基环树中环的大小，然后加上它树上最长子链长度就是答案，这里给出缩点后记忆化搜索的做法。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5+20;
int n,d[N],res=0;
int dfn[N],low[N],tot;
int stk[N],instk[N],top;
int scc[N],siz[N],cnt;
vector<int> h[N];
bool vis[N];
void tarjan(int x)
{
dfn[x]=low[x]=++tot;
stk[++top]=x,instk[x]=1;
for(auto v:h[x])
{
if(!dfn[v]) tarjan(v),low[x]=min(low[x],low[v]);
else if(instk[v]) low[x]=min(low[x],dfn[v]);
low[x]=min(low[x],dfn[v]);
}
if(dfn[x]==low[x]){
int y;
++cnt;
do{
y=stk[top--];
instk[y]=0;
scc[y]=cnt;
++siz[cnt];
}while(y!=x);
}
}
int dfs(int u)
{
vis[u]=1;
if(d[u]) return d[u];
d[u]++;
for(auto v:h[u])
{
if(vis[v]) continue;
vis[v]=1;
d[u]=max(d[u],dfs(v)+1);
}
return d[u];
}
signed main()
{
memset(d,0,sizeof d);
cin>>n;
for(int i=1;i<=n;i++){
int v;
cin>>v;
h[i].push_back(v);
}
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i);
for(int i=1;i<=n;i++){
int k=scc[i];
if(siz[k]>1) d[i]=siz[k];
}
for(int i=1;i<=n;i++){
memset(vis,0,sizeof vis);
res=max(res,dfs(i));
}
cout<<res;
}
