几只毛毛虫？

几只毛毛虫？

题目描述

一天，在生物课上，老师带着小羊和他的同学去公园观察动物。

他看到了草丛里有很多毛毛虫，于是他想，毛毛虫有什么特征呢？

于是他把一条毛毛虫抽象成了一棵有 $n$ 个节点的树。树是一个有 $n$ 个点 $n−1$ 条无向边组成的连通图。

这棵树被称为一条毛毛虫，当且仅当：树上存在一条路径 $u_1 \to u_2 \to \cdots →u_k$ $(k \geq 2)$ ，使得 $u_i, u_{i+1}$ $(1 \leq i < k)$ 有边，且 $u_1,u_2 , \ldots, u_k$ 两两不同；同时对于树上任一点 $v$ ，路径上存在一点到 $v$ 的距离不超过 $1$ 。

因为在 “是毛毛虫吗？” 中小羊画了太多毛毛虫，现在小羊觉得画毛毛虫太无聊了，于是他随便画了 $T$ 棵树，并一棵一棵地问你：用橡皮擦擦掉一些边和点的话，能形成多少只不同的毛毛虫呢？

只要两条毛毛虫包含了不同的节点，我们就认为这两条毛毛虫是不同的。

因为不同的毛毛虫的数量可能很多，请将答案关于 $10^9+7$ 取模后输出。

注意：我们认为单点不形成毛毛虫，因为找不到满足定义的路径。两条毛毛虫不同，当且仅当至少存在一个点在其中一条毛毛虫中，而不在另一条毛毛虫中。

输入描述:

第一行输入一个整数 $T (1 \leq T \leq 10^4)$ ，表示小羊画的树有 $T$ 棵。

接下来输入 $T$ 棵树。

对于每一棵树，第一行输入整数 $n$ $(2 \leq n \leq 10^5)$ ，表示这棵树的顶点的个数，这棵树的顶点为 $1,2, \ldots ,n$。

接下来的 $n−1$ 行，每行输入两个整数 $u_i,v_i$ $(1 \leq u_i, v_i \leq n)$ ，表示顶点 $u_i, v_i$ 之间连接了无向边。

保证输入的每一个图都是一棵树，且所有样例对应 $n$ 的和不超过 $2 \times 10^5$ 。

输出描述:

对于每一棵树，输出一行，在该行输出一个整数，表示该树通过擦去边和点，可以得到的不同的毛毛虫的数量，并将结果关于 $10^9 + 7$ 取模。

示例1

输入

2
4
1 2
2 3
2 4
4
1 2
2 3
3 4

输出

7
6

说明

对于第一棵树，以下顶点集和原图中集内点之间存在的边构成毛毛虫： 

$\{1,2\},\{2,3\},\{2,4\},\{1,2,3\},\{1,2,4\},\{2,3,4\},\{1,2,3,4\}$

对于第二棵树，以下顶点集和原图中集内点之间存在的边构成毛毛虫： 

$\{1,2\},\{2,3\},\{3,4\},\{1,2,3\},\{2,3,4\},\{1,2,3,4\}$

故答案分别为 $7,6$。

 

解题思路

  官方题解看了好久才看懂。题解写起来也挺麻烦的，要是有不懂的地方可以留言。

  容易知道，要判断一棵树是不是毛毛虫，可以选择树的直径作为题目定义中的路径，然后再判断所有点到直径的距离是否不超过 $1$ 即可。现在可以删除一些点和边，问有多少棵不同的树是毛毛虫，等价于问有多少个子图（也是一棵树）是毛毛虫。

  如果一个子图是毛毛虫，那么一定存在一条树的直径，而这条直径可以是树上任意一条路径。为此容易想到可以根据不同的路径作为直径来对子图分类。假设现在有一条路径，如果要以这条路径作为子图的直径，且这个子图是毛毛虫，应该满足什么条件？

  以下图为例，如果想让红色点所构成的路径作为子图的直径，那么该路径的两个端点的度数必须是 $1$（否则必然存在比该路径更长的直径），因此需要删除端点上除路径上节点外的其余所有点（也就是虚线三角形表示的子树）。接下来，要使得子图是毛毛虫，路径上非端点的点只能保留与其直接相邻的节点（即蓝色的点），否则会存在到该路径距离超过 $1$ 的节点。每个相邻节点可以选或不选。

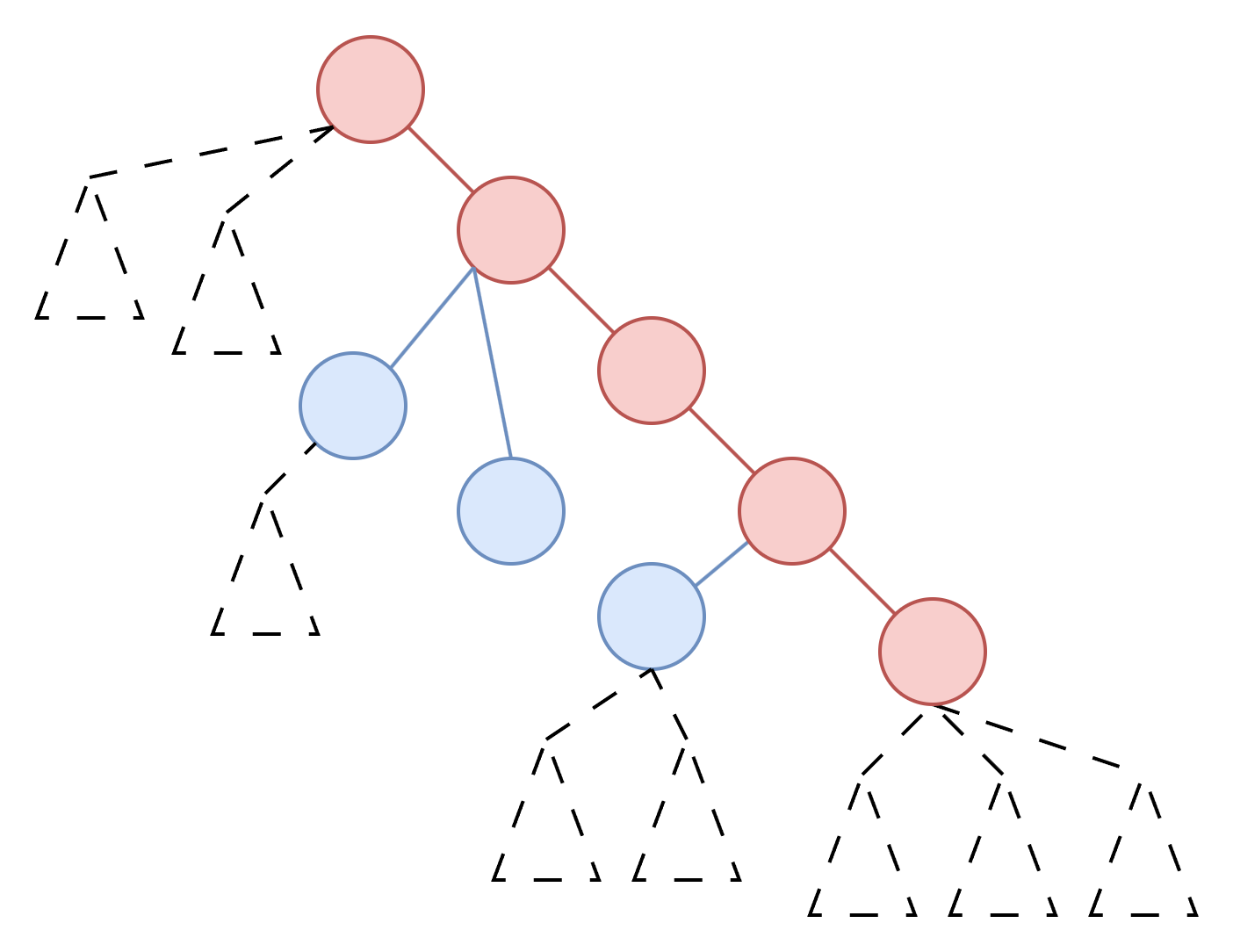
  当一条路径作为直径时，有多少个子图是毛毛虫呢？首先两个端点不能选除路径外的任何点，因此只有 $1$ 种方案。考虑路径上的非端点节点，假设一个节点 $u$ 的度数为 $d_u$，那么选择与其直接相邻的点的方案数为 $2^{d_u - 2}$（减 $2$ 是指不考虑路径上与其相邻的点，因为这个是必选的）。因此总的方案数是 $\sum\limits_{u}{2^{d_u - 2}}$，这里的 $u$ 是指路径上非端点的节点。

  但这种统计的方法会有重复，参考下图，两条不同的路径会得到同一个是毛毛虫的子图。

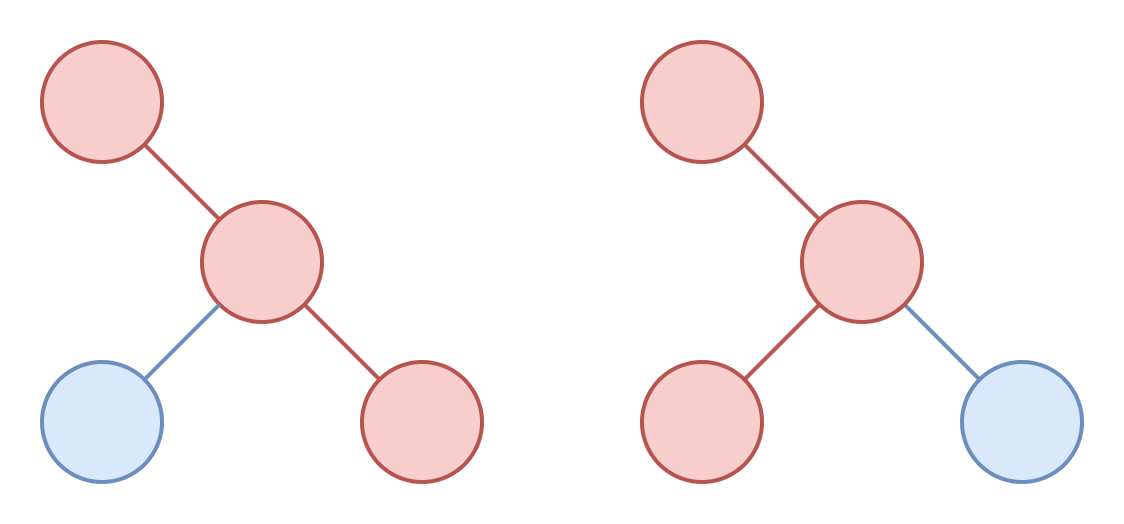
  可以发现与端点相邻的节点的统计方法会导致重复，因此我们可以参考官方题解中的方法，我们不要管直径的两个端点，而是选择直径上的非端点的节点。当然这条路径还是会存在两个端点的，不过要注意的是选出路径的端点在直径上是非端点节点，它们与直径的端点相连。此时路径的这两个端点的方案数应该都是 $2^{d_u-1}-1$，表示从直接与其相邻节点中（不含路径上与其相邻的另外一个节点）选出非空的方案数（因为要至少延伸出一个点作为直径的端点）。然后其余的每个节点的方案数还是 $2^{d_u - 2}$。

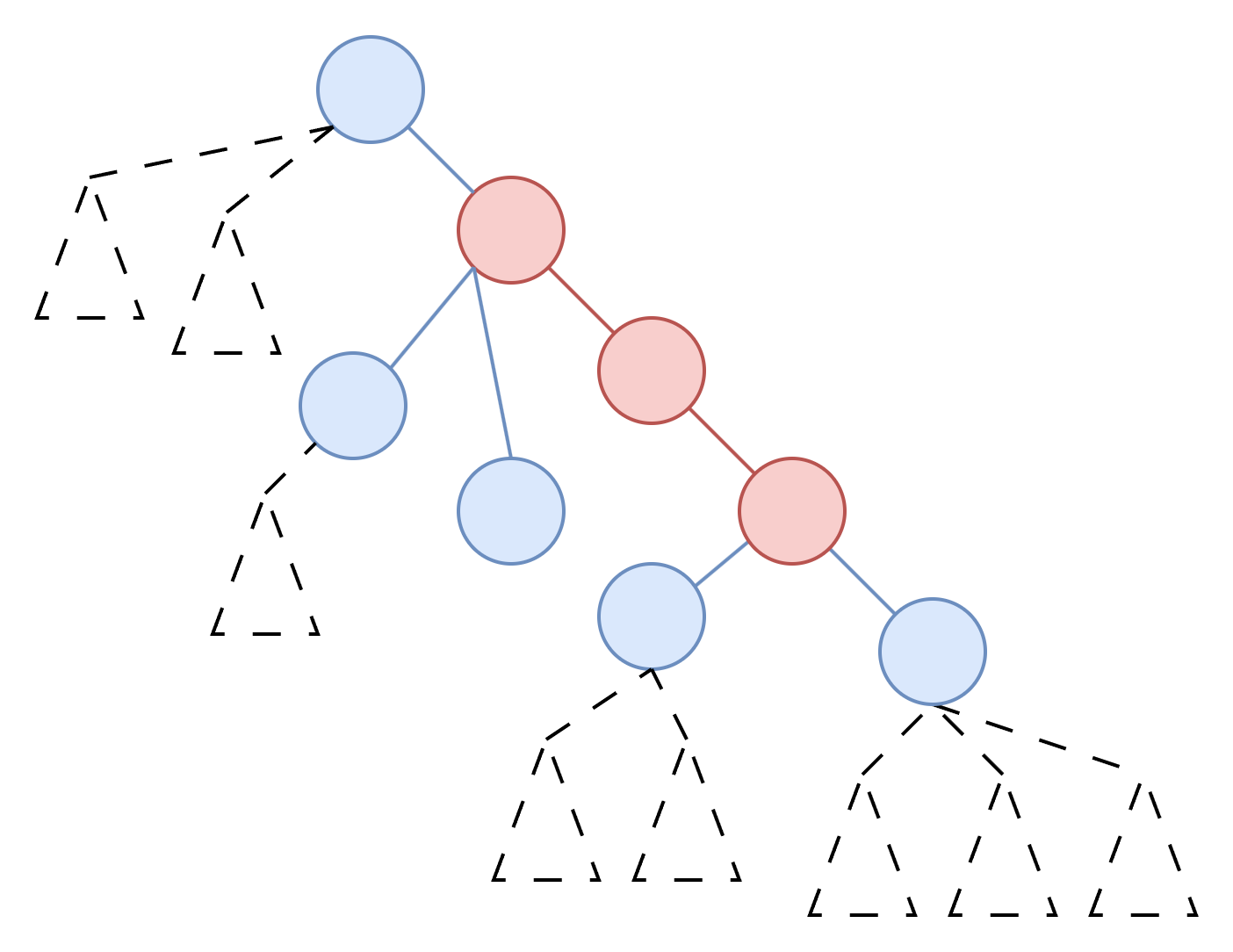
  因此我们可以枚举所有的路径，然后求出以该路径为直径的非端点节点，且构成毛毛虫的子图数量。所有路径的结果求和就是要求的答案。显然我们不可能真的枚举所有可能的路径，这样会超时。继续用分类的思想，将所有路径按照两个端点的 lca 进行分类（假设原树以节点 $1$ 为根）。接着就是遍历整个树，以每个节点 $u$ 作为路径两个端点的 lca 进行 dp。

  定义 $f(u)$ 表示 $u$ 与其子树中每个节点构成的链，作为直径上非端点节点时（其中子树中的节点与直径端点相连，而 $u$ 不与直径端点相连），方案数的和。太绕口了，看下面的图就明白了。

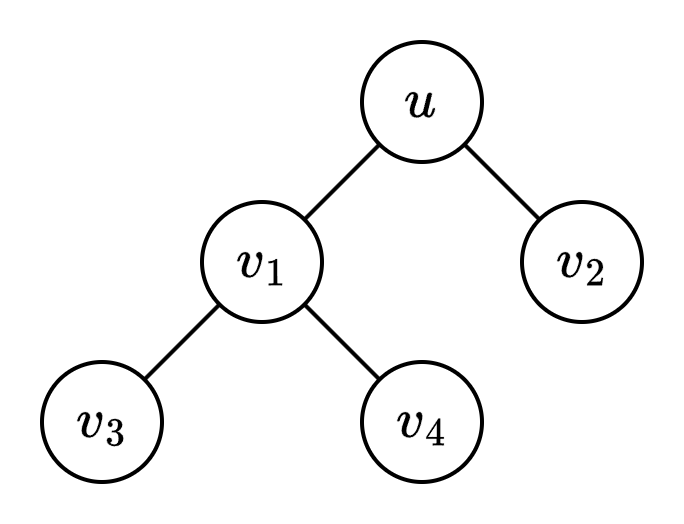
\begin{align*}
f(u)=2^{d_u-2} \times \left( (2^{d_{v_1}-1}-1) + (2^{d_{v_2}-1}-1) + 2^{d_{v_1}-2} \cdot (2^{d_{v_3}-1}-1) + 2^{d_{v_1}-2} \cdot (2^{d_{v_4}-1}-1) \right)
\end{align*}

  假设 $u$ 的儿子为 $v_1, v_2, \ldots v_m$。以 $u$ 作为两端点的 lca 的路径可以分成两类，第一类是以 $u$ 为端点的路径，方案数就是 $\sum\limits_{i=1}^{m}{(2^{d_u-1}-1) \cdot (f(v_i) + 2^{d_{v_i}-1}-1)}$。另一类是 $u$ 作为路径上的非端点的路径（意味着两个端点要从 $u$ 两个不同儿子的子树中选），方案数是 $\sum\limits_{i=2}^{m}{2^{d_u-2} \cdot (f(v_i) + 2^{d_{v_i}-1}-1) \left( \sum\limits_{j=1}^{i-1}{f(v_j) + 2^{d_{v_j}-1}-1} \right)}$（第二部分的求和可以用前缀和维护）。

  根据定义 $f(u) = 2^{d_u-2}\left(\sum\limits_{i=1}^{m}{f(v_i) + 2^{d_{v_i}-1}-1}\right)$。

  注意到上面的做法只能求出直径长度大于等于 $3$ 的毛毛虫子图数量。对于直径长度等于 $1$ 和 $2$ 的情况需要单独处理。

  其中当直径长度等于 $1$ 时，此时毛毛虫只能是两点一边的形式，这样的子图数量就是边的数量即 $n-1$。当直径长度等于 $2$ 时，此时直径应由三个节点构成，考虑直径中间的节点，那么直径长度为 $3$ 且子图是毛毛虫的方案数就是 $2^{d_{u}}-d_u-1$。其中 $2^{d_u}$ 表示选择 $u$ 与直接相邻节点的所有方案数，由于要保证直径的长度恰好为 $3$，因此要排除选择 $0$ 和 $1$ 个相邻节点的情况。

  剩下的细节可以看代码。  

  AC 代码如下，时间复杂度为 $O(n)$：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const int N = 2e5 + 5, M = N * 2, mod = 1e9 + 7;

int h[N], e[M], ne[M], idx;
int p2[N];
int d[N], f[N];
int ans;

void add(int u, int v) {
    e[idx] = v, ne[idx] = h[u], h[u] = idx++;
}

void dfs(int u, int p) {
    f[u] = 0;
    int sum = 0;
    for (int i = h[u]; i != -1; i = ne[i]) {
        int v = e[i];
        if (v == p) continue;
        dfs(v, u);
        ans = (ans + sum * (f[v] + p2[d[v] - 1] - 1ll) % mod * p2[d[u] - 2]) % mod;
        ans = (ans + (p2[d[u] - 1] - 1ll) * (f[v] + p2[d[v] - 1] - 1)) % mod;
        sum = (sum + f[v] + p2[d[v] - 1] - 1) % mod;
    }
    f[u] = 1ll * p2[d[u] - 2] * sum % mod;
}

void solve() {
    int n;
    cin >> n;
    memset(h, -1, n + 1 << 2);
    memset(d, 0, n + 1 << 2);
    idx = 0;
    for (int i = 0; i < n - 1; i++) {
        int u, v;
        cin >> u >> v;
        add(u, v), add(v, u);
        d[u]++, d[v]++;
    }
    p2[0] = 1;
    for (int i = 1; i <= n; i++) {
        p2[i] = p2[i - 1] * 2ll % mod;
    }
    ans = n - 1;
    for (int i = 1; i <= n; i++) {
        ans = (ans + p2[d[i]] - d[i] - 1) % mod;
    }
    dfs(1, 0);
    cout << (ans + mod) % mod << '\n';
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while (t--) {
        solve();
    }
    
    return 0;
}

 

参考资料

  小羊杯 Round 2 题解：https://blog.nowcoder.net/n/c5934ffa9a6d4c29b79cfaabb777aa3f