F1. Smooth Sailing (Easy Version)
F1. Smooth Sailing (Easy Version)
The only difference between the two versions of this problem is the constraint on $q$. You can make hacks only if both versions of the problem are solved.
Thomas is sailing around an island surrounded by the ocean. The ocean and island can be represented by a grid with $n$ rows and $m$ columns. The rows are numbered from $1$ to $n$ from top to bottom, and the columns are numbered from $1$ to $m$ from left to right. The position of a cell at row $r$ and column $c$ can be represented as $(r, c)$. Below is an example of a valid grid.
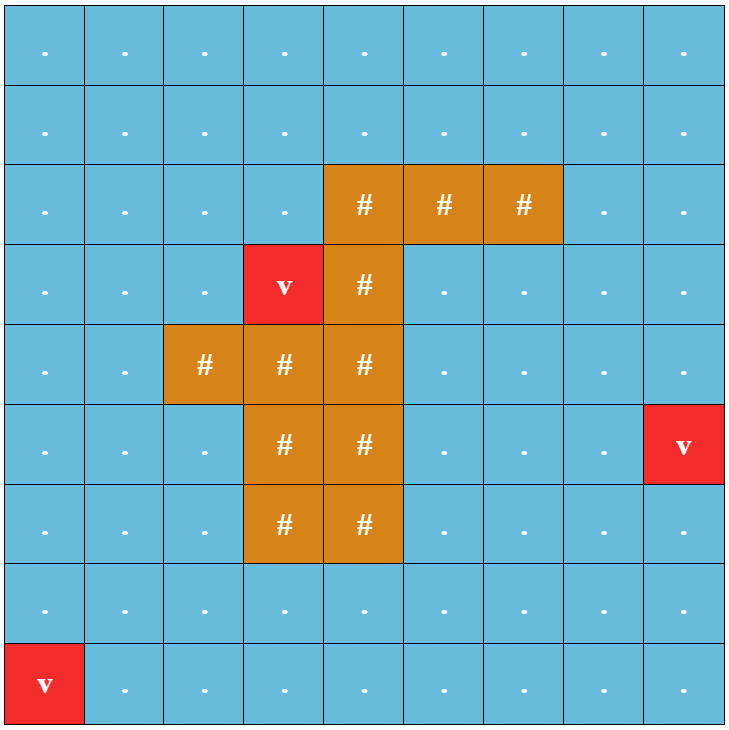
Example of a valid grid
There are three types of cells: island, ocean and underwater volcano. Cells representing the island are marked with a '#', cells representing the ocean are marked with a '.', and cells representing an underwater volcano are marked with a 'v'. It is guaranteed that there is at least one island cell and at least one underwater volcano cell. It is also guaranteed that the set of all island cells forms a single connected component$^{\dagger}$ and the set of all ocean cells and underwater volcano cells forms a single connected component. Additionally, it is guaranteed that there are no island cells at the edge of the grid (that is, at row $1$, at row $n$, at column $1$, and at column $m$).
Define a round trip starting from cell $(x, y)$ as a path Thomas takes which satisfies the following conditions:
- The path starts and ends at $(x, y)$.
- If Thomas is at cell $(i, j)$, he can go to cells $(i+1, j)$, $(i-1, j)$, $(i, j-1)$, and $(i, j+1)$ as long as the destination cell is an ocean cell or an underwater volcano cell and is still inside the grid. Note that it is allowed for Thomas to visit the same cell multiple times in the same round trip.
- The path must go around the island and fully encircle it. Some path $p$ fully encircles the island if it is impossible to go from an island cell to a cell on the grid border by only traveling to adjacent on a side or diagonal cells without visiting a cell on path $p$. In the image below, the path starting from $(2, 2)$, going to $(1, 3)$, and going back to $(2, 2)$ the other way does not fully encircle the island and is not considered a round trip.
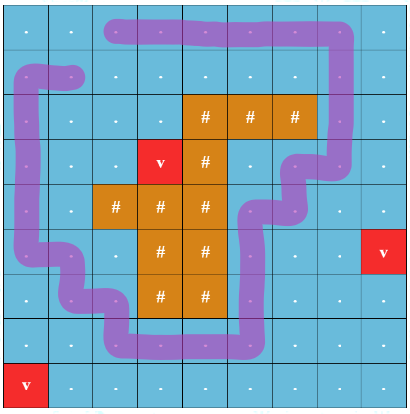
Example of a path that does not fully encircle the island
The safety of a round trip is the minimum Manhattan distance$^{\ddagger}$ from a cell on the round trip to an underwater volcano (note that the presence of island cells does not impact this distance).
You have $q$ queries. A query can be represented as $(x, y)$ and for every query, you want to find the maximum safety of a round trip starting from $(x, y)$. It is guaranteed that $(x, y)$ is an ocean cell or an underwater volcano cell.
$^{\dagger}$A set of cells forms a single connected component if from any cell of this set it is possible to reach any other cell of this set by moving only through the cells of this set, each time going to a cell with a common side.
$^{\ddagger}$Manhattan distance between cells $(r_1, c_1)$ and $(r_2, c_2)$ is equal to $|r_1 - r_2| + |c_1 - c_2|$.
Input
The first line contains three integers $n$, $m$, and $q$ ($3 \leq n, m \leq 10^5$, $9 \leq n \cdot m \leq 3 \cdot 10^5$, $1 \leq q \leq 5$) — the number of rows and columns of the grid and the number of queries.
Each of the following $n$ lines contains $m$ characters describing the cells of the grid. The character '#' denotes an island cell, '.' denotes an ocean cell, and 'v' denotes an underwater volcano cell.
It is guaranteed that there is at least one island cell and at least one underwater volcano cell. It is guaranteed that the set of all island cells forms a single connected component and the set of all ocean cells and underwater volcano cells forms a single connected component. Also, it is guaranteed that there are no island cells at the edge of the grid (that is, at the row $1$, at the row $n$, at the column $1$, and at the column $m$).
The following $q$ lines describe the queries. Each of these lines contains two integers $x$ and $y$ ($1 \leq x \leq n$, $1 \leq y \leq m$) denoting a round trip starting from $(x, y)$.
It is guaranteed that $(x, y)$ is an ocean cell or an underwater volcano cell.
Output
For each query, output a single integer — the maximum safety of a round trip starting from the specified position.
Examples
input
9 9 3
.........
.........
....###..
...v#....
..###....
...##...v
...##....
.........
v........
1 1
9 1
5 7output
3
0
3input
3 3 5
..v
.#.
...
1 2
1 3
2 3
2 1
3 2output
0
0
0
0
0input
14 13 5
.............
.............
.............
...vvvvvvv...
...v.....v...
...v.###.v...
...v.#.#.v...
...v..v..v...
...v..v..v...
....v...v....
.....vvv.....
.............
.............
.............
1 1
7 7
5 6
4 10
13 6output
3
0
1
0
2input
10 11 4
...........
..#######..
..#..#..#..
..#.....#..
..#..v..#..
..#.###.#..
..#.#.#.#..
..#...#.#..
..#####.#..
...........
7 6
3 7
6 8
1 1output
1
2
3
4Note
For the first example, the image below shows an optimal round trip starting from $(1, 1)$. The round trip has a safety of $3$ as the minimum Manhattan distance from a cell on the round trip to an underwater volcano is $3$.
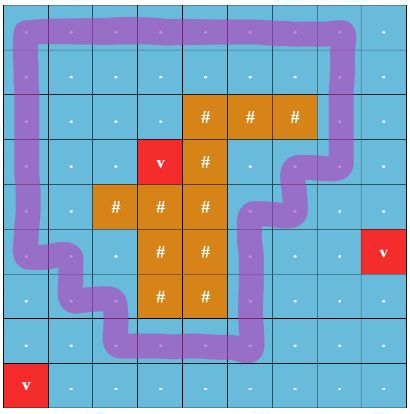
Example of an optimal round trip
For the fourth example, remember that it is allowed for Thomas to visit the same cell multiple times in the same round trip. For example, doing so is necessary for the round trip starting from $(7, 6)$.
解题思路
容易知道答案具有二段性,所以考虑二分答案。对于二分值 $d$,我们只能访问距离所有 v 至少为 $d$ 的格子,这样才能保证最后访问的所有格子距离 v 的最小值至少为 $d$,即答案为 $d$。所以只需找到满足该条件且与询问 $(x,y)$ 连通的格子,并判断能否把所有的 # 包围住。
为了判断某个格子是否满足距离所有的 v 都至少为 $d$,可以用多源 bfs,即把所有 v 的格子压入队列进行 bfs,最后得到的 $\text{dist}$ 数组就是每个格子距离所有的 v 的最小值。因此合法的格子就要满足 $\text{dist}_{i,j} \geq d$。
而找到所有与 $(x,y)$ 连通的格子则有很多方法,可以从 $(x,y)$ 开始进行 dfs 或 bfs,往上下左右四个方向的合法的格子扩展。或者用并查集,只需枚举每个格子,把四个方向中合法的格子与该格子合并,最后如果 $(i,j)$ 与 $(x,y)$ 在同一个连通块内则有 find({i,j}) = find({x,y})。
最后是判断 $(x,y)$ 所在的连通块能否将所有的 # 包围。反过来思考,某个 # 能否在不访问 $(x,y)$ 连通块内格子的前提下到达边缘处?如果可以则说明则无法将所有的 # 包围,否则可以。因此做法就是随便找一个 # 的格子压入队列进行 bfs(当然也可以 dfs),每次往 $8$ 个方向扩展(除了上下左右外,还要考虑左上、右上、左下和右下),只要扩展的格子之前没被遍历过以及不在 $(x,y)$ 所在的连通块内,就把它压入队列。其中如果在扩展的过程中发现可以扩展到边缘处,则说明无法将 # 包围。
之所以要往 $8$ 个方向扩展是为了判断下图中未包围的情况,即可以从 $(2,3)$ 走到边缘处 $(1,2)$。

AC代码如下,时间复杂度为 $O(q \cdot nm)$:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10, M = 3e5 + 10;
int n, m, k, sx, sy;
string g[N];
vector<int> dist[N];
int dx[8] = {-1, 0, 1, 0, -1, -1, 1, 1}, dy[8] = {0, 1, 0, -1, -1, 1, 1, -1};
int fa[M];
vector<bool> vis[N];
int find(int x) {
return fa[x] == x ? fa[x] : fa[x] = find(fa[x]);
}
bool check(int d) {
iota(fa, fa + n * m, 0);
queue<array<int, 2>> q;
// 找到所有连通块
for (int i = 0; i < n; i++) {
vis[i].assign(m, false);
for (int j = 0; j < m; j++) {
if (g[i][j] == '#' && q.empty()) { // 随便找到一个是#的格子
q.push({i, j});
vis[i][j] = true;
}
if (g[i][j] != '#' && dist[i][j] >= d) { // 往四个方向合并
for (int k = 0; k < 4; k++) {
int x = i + dx[k], y = j + dy[k];
if (x < 0 || x >= n || y < 0 || y >= m) continue;
if (g[x][y] == '#') continue;
if (dist[x][y] < d) continue; // 格子到v的距离小于d不合法
fa[find(x * m + y)] = find(i * m + j);
}
}
}
}
// 判断从#出发能否到达边缘处
while (!q.empty()) {
auto p = q.front();
q.pop();
for (int i = 0; i < 8; i++) {
int x = p[0] + dx[i], y = p[1] + dy[i];
if (x < 0 || x >= n || y < 0 || y >= m) continue;
if (find(x * m + y) == find(sx * m + sy)) continue; // 不能访问(x,y)连通块中的格子
if (!x || x == n - 1 || !y || y == m - 1) return false; // 可以访问边缘处,无法包围#
if (vis[x][y]) continue;
vis[x][y] = true;
q.push({x, y});
}
}
return true;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> k;
for (int i = 0; i < n; i++) {
cin >> g[i];
}
// 把所有是v的格子压入队列
queue<array<int, 2>> q;
for (int i = 0; i < n; i++) {
dist[i].assign(m, 0x3f3f3f3f);
for (int j = 0; j < m; j++) {
if (g[i][j] == 'v') {
q.push({i, j});
dist[i][j] = 0;
}
}
}
// 求每个格子到v的最短距离
while (!q.empty()) {
auto p = q.front();
q.pop();
for (int i = 0; i < 4; i++) {
int x = p[0] + dx[i], y = p[1] + dy[i];
if (x < 0 || x >= n || y < 0 || y >= m) continue;
if (dist[x][y] > dist[p[0]][p[1]] + 1) {
dist[x][y] = dist[p[0]][p[1]] + 1;
q.push({x, y});
}
}
}
// 二分答案
while (k--) {
cin >> sx >> sy;
sx--, sy--;
int l = 0, r = n + m;
while (l < r) {
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
cout << l << '\n';
}
return 0;
}
参考资料
Editorial for Codeforces Round #919 (Div. 2):https://codeforces.com/blog/entry/122560
本文来自博客园,作者:onlyblues,转载请注明原文链接:https://www.cnblogs.com/onlyblues/p/17983158



 浙公网安备 33010602011771号
浙公网安备 33010602011771号