【AtCoder】ARC082 F - Sandglass

【链接】F - Sandglass

【题意】给定沙漏A和B，分别装着a和X-a的沙子，开始时A在上B在下，每秒漏1，漏完不再漏。给定n，有n个时刻ai沙漏倒转。给定m个询问，每次询问给定初值a和时刻t，求A中沙子量。

【算法】数学（函数）

【题解】

先不考虑时刻，令ft(a)表示沙子初值a时，当前A中的沙子数。（x轴是初值a，y轴是沙子数num）

时刻为0时，显然是一条从0出发斜率为1的直线。

若A在上，则每过1s，整段函数都下移一个单位，碰到y=0则变成平的。

若A在下，则每过1s，整段函数都上移一个单位，碰到y=X则变成平的。

而不平的部分，斜率恒为1。

这样，这个函数始终是一个三段函数，可以按时间顺序维护两个转折点的位置就可以快速出解。

复杂度O(m)。

然而这个函数还有一些特殊的性质，所以可以更方便地写程序。

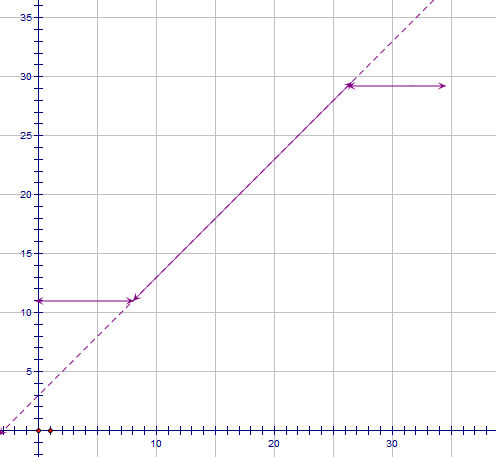
我们维护斜率为1的原y=x+b，其中b就是变化量，这样f(A)就是A+b，判断一下A+b和两个转折点y值的关系即可。

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=100010;
int n,m,a[maxn];
int calc(int l,int r,int x)
{return max(l,min(r,x));}
int main(){
    int X;
    scanf("%d%d",&X,&n);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    int L,R=X;//初值……
    int t=0,k=0,s=-1,x=0;
    int time,A;
    scanf("%d",&m);
    for(int i=1;i<=m;i++){
        scanf("%d%d",&time,&A);
        while(k<n&&a[k+1]<=time){
            int dif=s*(a[k+1]-t);
            L=calc(0,X,L+dif);
            R=calc(0,X,R+dif);
            s*=-1;
            x+=dif;
            t=a[k+1];
            k++;
        }
        int T=time-t;
        A=calc(L,R,A+x);
        A=calc(0,X,A+s*T);
        printf("%d\n",A);
    }
    return 0;
}