[ICPC] 2021济南E.Insidemen

一道比较考思维的题，赛场上没有写出来，赛后来补发现可做。
分类讨论的情况比较多。

题意：
一个圆上顺时针排列\(1\dots n\)号点，然后给定\(M\)条边，每条边连接\(x,y\)点。两条边\((a,b)(c,d)\)假如严格交于圆内，则造成\((a+b)*(c+d)\)的贡献，现在要删除2个点和这2个点所有的连边，问剩余的贡献最大为多少。
\(n\le 1000, m\le 10^5\)
解法：
其实赛场上看到这道题第一想法就是一个类似数据结构的题，大题思路是对的，不过需要很多讨论和优化，加之没有队伍通过该题，遂弃之。

我们考虑一条线上的交点是怎么得出的。
这条线将圆分成两边，从左半到右半有连边构成交点，边的二元关系，就是一个笛卡尔积，显然是邻接矩阵上的一块区域，可以维护一个二维前缀和，可以快速求出\(t = \sum_{s\in[a,b],t\in[c,d]}(s+t)\)，那么这条边\((i, j)\)的贡献就是\(t\times (i + j)\)。

我们把每条边的贡献加起来除2，就是不删除点的贡献和。
然后我们考虑删除一个点，造成的负贡献。

我们枚举相交的边，如图，图中红线为枚举的边。

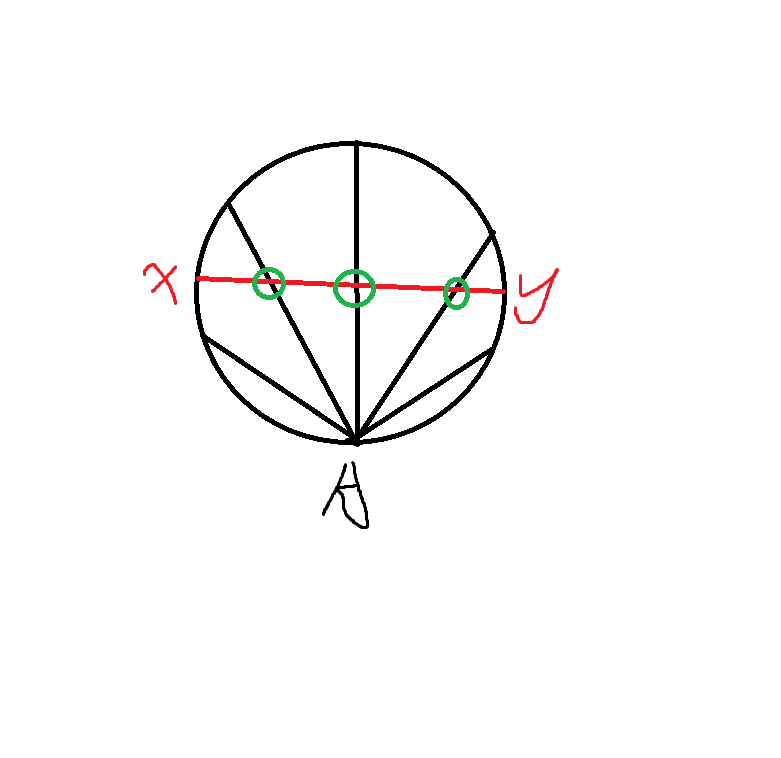
显然二维前缀和可以搞出这条线与\(<B\in(x,y),A>\)这些边的贡献。枚举边的所有贡献和就是删掉\(A\)点的负贡献。

发现当删除\(A,B\)时，贡献等于总贡献减去\(A,B\)的负贡献，再把\(A,B\)共同造成的贡献加回来，问题就是求\(A,B\)共同造成的贡献。

其实求单点负贡献也可以顺便求出\(A\)点和每个点的共同贡献，只需要枚举线的时候，把这条线的贡献累加到x,y上，于是我们求出了任意一点与A不直接相连的贡献数，接下来考虑一个点与A直接相连这条边的贡献就很简单了，就是左半圆到右半圆的笛卡尔积，这一步与上面求总贡献是一样的。

然后枚举删除点对的最大贡献值就是答案。

代码：

#include <bits/stdc++.h>
#define int long long
#define pt(x) cout << x << endl;
#define Mid ((l + r) / 2)
#define lson (rt << 1)
#define rson (rt << 1 | 1)
using namespace std;
const int N = 1009, M = 1e5 + 1009;
int n, m, g[N][N], times[N], sum[N];
struct node {
	int x, y;
} a[M];
int query(int x, int y, int xx, int yy) {
	if(x > xx) return 0;
	if(y > yy) return 0;
	return g[xx][yy] - g[x - 1][yy] - g[xx][y - 1] + g[x - 1][y - 1];
}
int cal(int x, int y) {
	if(query(x, y, x, y) == 0) return 0;
	if(x > y) swap(x, y);
	return query(x + 1, y + 1, y - 1, n) + query(x + 1, 1, y - 1, x - 1);
}
signed main()
{
	ios :: sync_with_stdio(0);
	cin.tie(0);
	cin >> n >> m;
	for(int i = 1; i <= m; i++) {
		int x, y;
		cin >> x >> y;
		a[i].x = x; a[i].y = y;
		if(a[i].x > a[i].y) swap(a[i].x, a[i].y);
		g[x][y] += x + y;
		g[y][x] += x + y;
	}
	for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) g[i][j] += g[i - 1][j];
	for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) g[i][j] += g[i][j - 1];
	int tot = 0;
	for(int i = 1; i <= m; i++) {
		tot += (a[i].x + a[i].y) * cal(a[i].x, a[i].y);
	}
	tot /= 2;
	int ans = 0;
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) if(a[j].x != i && a[j].y != i) {
			if(a[j].y == a[j].x + 1) continue;
			int inter = 0;
			if(i > a[j].x && i < a[j].y) {
				inter = query(i, 1, i, a[j].x - 1);
				inter += query(i, a[j].y + 1, i, n);
			} else {
				inter = query(i, a[j].x + 1, i, a[j].y - 1);
			}
			sum[i] += inter * (a[j].x + a[j].y);
		}
	}
	for(int i = 1; i <= n; i++) {
		memset(times, 0, sizeof(times));
		for(int j = 1; j <= m; j++) if(a[j].x != i && a[j].y != i) {
			if(a[j].y == a[j].x + 1) continue;
			int inter = 0;
			if(i > a[j].x && i < a[j].y) {
				inter = query(i, 1, i, a[j].x - 1);
				inter += query(i, a[j].y + 1, i, n);
			} else {
				inter = query(i, a[j].x + 1, i, a[j].y - 1);
			}
			times[a[j].x] += inter * (a[j].x + a[j].y);
			times[a[j].y] += inter * (a[j].x + a[j].y);
		}
		for(int j = 1; j <= n; j++) if(i != j) {
			ans = max(ans, tot - sum[i] - sum[j] + times[j] + (i + j) * cal(i, j));
		}
	}
	cout << ans << endl;
	return 0;
}