最近公共祖先（LCA）
「观前提醒」
「文章仅供学习和参考，如有问题请在评论区提出」
前言
简单的模板整理，只是概括了一下具体的实现方法（说到底是给自己写的），如果看不明白可以去看原视频（讲的很好），链接在参考资料里。
定义
最近公共祖先简称 \(LCA\)（Lowest Common Ancestor）。在一个树上，两个节点的最近公共祖先，就是这两个点的公共祖先里，离树根最远的那个。
例如，\(6\) 与 \(8\) 的最近公共祖先为 \(1\) ，\(5\) 和 \(3\) 的最近公共祖先为 \(5\) 。
性质
- \(u\) 是 \(v\) 的祖先，当且仅当 \(LCA(u, v) = u\) 。
- 如果 \(u\) 不为 \(v\) 的祖先，并且 \(v\) 不为 \(v\) 的祖先，那么 \(u, v\) 分别处于 \(LCA(u, v)\) 的两颗不同子树上。
- 两点的最近公共祖先必定处在树上两点间的最短路上。
- \(d(u, v) = h(u) + h(v) - 2h(LCA(u, v))\) ，其中 \(d\) 是树上两点间的距离，\(h\) 代表某点到树根的距离。
求 LCA
倍增算法
倍增算法是最经典的求 \(LCA\) 的算法。
在倍增算法里，我们需要维护
-
g[u]：存无向图（树） -
dep[u]：存 \(u\) 的深度（默认树根的深度为 \(1\) ） -
fa[u][i] ：存从 \(u\) 点向树根跳 \(2^{i}\) 层的祖先节点（就是跳 \(2^{i}\) 层所能到达的节点）。如果在跳跃的时候超过了树根，就默认为 \(0\) 。
然后我们通过 dfs() ，从树根开始遍历，然后对每个 \(u\) 进行 dep[u] 和 fa[u][i] 的推导。
对于 dep[u] 的推导就是 dep[u] = dep[father] + 1; ；
对于 fa[u][i] 的推导就是 fa[fa[u][i - 1]][i - 1] ，这里就是让 \(u\) 先向树根跳 \(2^{i - 1}\) 步，得到一个祖先节点（半路的），然后通过这个祖先节点再跳 \(2^{i - 1}\) 步，来获得 fa[u][i] 的值。
对于每趟 dfs() 都需要这样倍增地去推导 fa[u][i] ，而每次推导最多需要 \(logN\) 次，所以整个预处理的时间复杂度就是 \((n + m)logn\) 。
预处理完后，先根据 dep[u] 来判断连个节点的深度，然后先让深度大的跳到与另一个同一深度。然后两个节点再统一向上跳，知道两点相遇（跳到的祖先节点相同），相遇的节点就是最近公共祖先的位置。
时间复杂度
- 预处理：\(O(nlogn)\)
- 查询：\(O(logn)\)
- 总体：\(O((n + m)logn)\)
模板代码
const int N = 5e5 + 10;
int dep[N]; // u 节点的深度
int fa[N][22]; // 从 u 节点向树根跳 2^i 步所能到达的祖先节点
vector<int> g[N]; // 存图
// 当前节点 u, 它的父节点为 f
void dfs(int u, int f) {
dep[u] = dep[f] + 1; // 更新深度
fa[u][0] = f;
for (int i = 1; i <= 20; i++) // 更新每一个 fa[u][i]
fa[u][i] = fa[fa[u][i - 1]][i - 1];
for (auto v : g[u])
if (v != f) dfs(v, u);
}
int lca(int u, int v) {
if (dep[u] < dep[v]) swap(u, v); // 让 u 为深度大的那个, 为了好处理
for (int i = 20; i >= 0; i--) // 从大步跳到逐渐跳小步
if (dep[fa[u][i]] >= dep[v]) // 保证 u 的深度低于 v
u = fa[u][i]; // u 向上跳 2^i 步
if (u == v) // 如果此时 u 和 v 相同，说明 u 和 v 在同一条树链上
return v; // 此时 v 就是 两者的最近公共祖先
for (int i = 20; i >= 0; i--) // 同样是从大步跳到逐渐跳小步
if (fa[u][i] != fa[v][i]) // 如果两者没相遇
u = fa[u][i], v = fa[v][i]; // 就继续同时向上跳
// 最后 u 和 v 都停在最近公共祖先的下面一层
return fa[u][0]; // 返回时再网上跳一层就行了
}
// 调用
dfs(root, 0); // root 根节点
int Lca = lca(u, v);
Trajan 算法
Trajan算法是一种离线算法，巧妙地利用并查集来维护祖先节点。它是先把所有的询问请求都存先来，然后统一求解，所以是离线的。
在 \(Trajan\) 算法里，我们需要维护，
g[u]：存无向图（树，必须是无向图）query[u]：所有与 \(u\) 有关联的查询请求f[u]：存 \(u\) 的父节点（并查集）vis[u]：打标记，用来判断是否走过ans[i]：用来存储查询结果
从根节点开始 dfs() ，然后对当前节点打上标记，表示已经走过了。然后逐一枚举遍历自己的儿子节点，每一个儿子在回溯的时候再让儿子的父节点脸上 \(u\) ，即 f[v] = u; 。
然后当遍历完自身所有的儿子节点后，以 \(u\) 为起点查询 query[u] ，如果查到 \(v\) 被走过，那就用并查集查找 \(v\) 的根节点，那么此时的 \(LCA(u, v) = find(v)\) 。
因为并查集是跟着 dfs() 一点一点建立起来的，在建立的过程中我们用并查集去查找的话，就只会查找到最近的且是同一个祖先节点的地方。
时间复杂度
- 整个处理：\(O(n + m)\)
模板代码
typedef pair<int, int> PII;
const int N = 5e5 + 10;
vector<int> g[N]; // 存树
vector<PII> query[N]; // 存询问，用pair是要再存储询问的编号，来进行ans的赋值
int f[N]; // 存父节点
bool vis[N]; // 打标记，判断是否走过
int ans[N]; // 存查询结果
int n, m, root;
// 初始化
void init() {
cin >> n >> m >> root;
for (int i = 1; i <= n; i++) f[i] = i;
for (int i = 1; i < n; i++) { // 建图
int u, v;
scanf("%d%d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}
for (int i = 1; i <= m; i++) { // 存请求
int u, v;
scanf("%d%d", &u, &v);
query[u].push_back({v, i}); // 一定要建双向的
query[v].push_back({u, i});
}
}
// 并查集查询
int find(int x) {
if (f[x] != x) f[x] = find(f[x]);
return f[x];
}
// Trajan算法
void trajan(int u) {
vis[u] = true; // 打标记
for (auto v : g[u]) { // 遍历儿子节点
if (!vis[v]) {
trajan(v);
f[v] = u; // 每个儿子节点回溯时进行并查集合并
}
}
for (auto it : query[u]) { // 遍历所有和 u 相关的询问
int v = it.first, cnt = it.second;
if (vis[v]) // 如果遍历过
ans[cnt] = find(v); // 答案就是 v 在并查集里的根节点
}
}
// 调用
init();
tarjan(root); // root 是根节点
// 最后输出结果就行
for (int i = 1; i <= m; i++)
cout << ans[i] << "\n";
树链剖分
基本概念
重儿子：父节点的所有儿子中子树节点数目最多的节点。
轻儿子：父节点中除重儿子以外的儿子。
重边：父节点和重儿子连成的边
重链：由多条重边连接而成的路径。
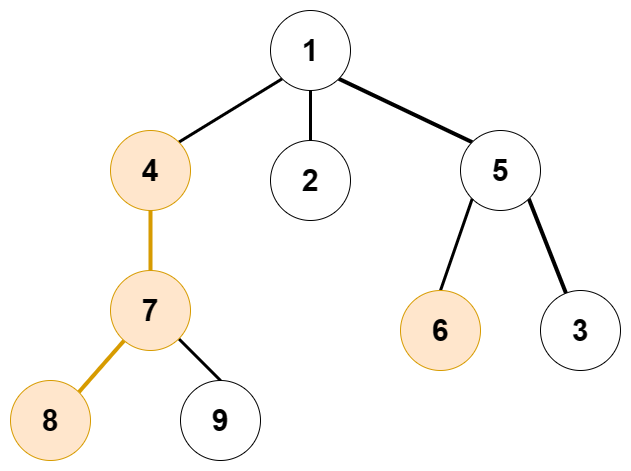
基本性质
- 整棵树会被剖分成若干条重链。
- 轻儿子一定是每条重链的顶点。
- 任意一条路径被切分成不超过 \(logn\) 条链。
具体实现
在树链剖分的思路里，我们需要维护，
g[u]：存树fa[u]：存 \(u\) 的父节点son[u]：存 \(u\) 的重儿子sz[u]：存以 \(u\) 为根节点的子树的节点数top[u]：存 \(u\) 所在重链的顶点
先跑一遍 dfs() 来预处理 fa[u], dep[u], son[u] ，然后再跑一遍 dfs() 来处理出 top[u] 。
预处理完在求解的时候，只需要让两个节点沿着各自的重链向上跳，当它们跳到同一条重链上时，深度较小的那个节点就是它们的 \(LCA\) 。
因为是沿着重链跳，重链最多有 \(logn\) 条，那么最多会跳 \(logn\) 次，所以每次查询的时间复杂度就是 \(O(logn)\) 。
时间复杂度
- 预处理：\(O(n)\)
- 查询：\(O(logn)\)
- 总体：\(O(n + mlogn)\)
模板代码
const int N = 5e5 + 10;
vector<int> g[N]; // 存树
int fa[N]; // 存 u 的父节点
int dep[N]; // 存 u 的深度
int son[N]; // 存 u 的重儿子
int sz[N]; // 存以 u 为根的子树的节点数
int top[N]; // 存 u 所在重链的顶点
// 预处理出 fa[], dep[], son[], sz[]
void dfs1(int u, int f) {
fa[u] = f, dep[u] = dep[f] + 1, sz[u] = 1;
for (auto v : g[u]) {
if (v == f) continue;
dfs1(v, u);
sz[u] += sz[v];
if (sz[son[u]] < sz[v]) son[u] = v;
}
}
// 预处理出 top[]
void dfs2(int u, int t) {
top[u] = t;
if (!son[u]) return; // 如果没有重儿子就返回
dfs2(son[u], t); // 遍历重儿子
for (auto v : g[u]) { // 遍历轻儿子
if (v == fa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
// 求 u 和 v 的 LCA
int lca(int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) swap(u, v);
u = fa[top[u]];
}
// 最后深度低的就是LCA
if (dep[u] < dep[v]) return u;
return v;
}
// 使用
dfs1(root, 0); // root 是根节点
dfs2(root, 0);
int Lca = lca(u, v);
