PTA 21级数据结构与算法实验7—查找表
7-1 电话聊天狂人
给定大量手机用户通话记录,找出其中通话次数最多的聊天狂人。
输入格式:
输入首先给出正整数N(≤105),为通话记录条数。随后N行,每行给出一条通话记录。简单起见,这里只列出拨出方和接收方的11位数字构成的手机号码,其中以空格分隔。
输出格式:
在一行中给出聊天狂人的手机号码及其通话次数,其间以空格分隔。如果这样的人不唯一,则输出狂人中最小的号码及其通话次数,并且附加给出并列狂人的人数。
输入样例:
4
13005711862 13588625832
13505711862 13088625832
13588625832 18087925832
15005713862 13588625832
输出样例:
13588625832 3
代码 :
#include <bits/stdc++.h>
using namespace std;
map<string, int> mp;
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
string a, b;
cin >> a >> b;
mp[a]++, mp[b]++;
}
string a;
int num = 0;
int sum = 0;
for (auto it : mp) {
if (it.second > num) {
a = it.first;
num = it.second;
sum = 1;
} else if (it.second == num) sum++;
}
cout << a << " " << num;
if (sum != 1) cout << " " << sum << endl;
return 0;
}
7-2 两个有序序列的中位数
已知有两个等长的非降序序列S1, S2, 设计函数求S1与S2并集的中位数。有序序列A0,A1,⋯,AN−1 的中位数指A(N−1)/2的值,即第⌊(N+1)/2⌋个数(A0为第1个数)。
输入格式:
输入分三行。第一行给出序列的公共长度N(0<N≤100000),随后每行输入一个序列的信息,即N个非降序排列的整数。数字用空格间隔。
输出格式:
在一行中输出两个输入序列的并集序列的中位数。
输入样例1:
5
1 3 5 7 9
2 3 4 5 6
输出样例1:
4
输入样例2:
6
-100 -10 1 1 1 1
-50 0 2 3 4 5
输出样例2:
1
代码 :
#include <bits/stdc++.h>
using namespace std;
vector<int> v;
int main() {
int n;
cin >> n;
for (int i = 0; i < 2 * n; i++) {
int x;
cin >> x;
v.push_back(x);
}
sort(v.begin(), v.end());
cout << v[(v.size() - 1) / 2] << endl;
return 0;
}
7-3 词频统计
请编写程序,对一段英文文本,统计其中所有不同单词的个数,以及词频最大的前10%的单词。
所谓“单词”,是指由不超过80个单词字符组成的连续字符串,但长度超过15的单词将只截取保留前15个单词字符。而合法的“单词字符”为大小写字母、数字和下划线,其它字符均认为是单词分隔符。
输入格式:
输入给出一段非空文本,最后以符号#结尾。输入保证存在至少10个不同的单词。
输出格式:
在第一行中输出文本中所有不同单词的个数。注意“单词”不区分英文大小写,例如“PAT”和“pat”被认为是同一个单词。
随后按照词频递减的顺序,按照词频:单词的格式输出词频最大的前10%的单词。若有并列,则按递增字典序输出。
输入样例:
This is a test.
The word "this" is the word with the highest frequency.
Longlonglonglongword should be cut off, so is considered as the same as longlonglonglonee. But this_8 is different than this, and this, and this...#
this line should be ignored.
输出样例:(注意:虽然单词the也出现了4次,但因为我们只要输出前10%(即23个单词中的前2个)单词,而按照字母序,the排第3位,所以不输出。)
23
5:this
4:is
代码 :
#include <bits/stdc++.h>
using namespace std;
map<string, int> mp;
vector<pair<int, string>> v;
bool cmp(pair<int, string> a, pair<int, string> b) {
if (a.first != b.first) return a.first > b.first;
return a.second < b.second;
}
int main() {
string s = "";
char c;
while (~scanf("%c", &c)) {
if (c >= 'A' && c <= 'Z' || c >= 'a' && c <= 'z' || c >= '0' && c <= '9' || c == '_') {
if (c >= 'A' && c <= 'Z') c = c - 'A' + 'a';
if (s.size() < 15) s += c;
} else {
if (!s.empty()) mp[s]++, s = "";
if (c == '#') break;
}
}
for (auto it : mp) {
v.push_back({it.second, it.first});
}
sort(v.begin(), v.end(), cmp);
int n = v.size() / 10;
cout << v.size() << endl;
for (int i = 0; i < n; i++) cout << v[i].first << ":" << v[i].second << endl;
return 0;
}
7-4 集合相似度
给定两个整数集合,它们的相似度定义为:N**c/N**t×100%。其中N**c是两个集合都有的不相等整数的个数,N**t是两个集合一共有的不相等整数的个数。你的任务就是计算任意一对给定集合的相似度。
输入格式:
输入第一行给出一个正整数N(≤50),是集合的个数。随后N行,每行对应一个集合。每个集合首先给出一个正整数M(≤104),是集合中元素的个数;然后跟M个[0,109]区间内的整数。
之后一行给出一个正整数K(≤2000),随后K行,每行对应一对需要计算相似度的集合的编号(集合从1到N编号)。数字间以空格分隔。
输出格式:
对每一对需要计算的集合,在一行中输出它们的相似度,为保留小数点后2位的百分比数字。
输入样例:
3
3 99 87 101
4 87 101 5 87
7 99 101 18 5 135 18 99
2
1 2
1 3
输出样例:
50.00%
33.33%
理解 :
Nc : 两个集合间相同的数字, 但是不会重复计算
Nt : 就是两个集合合并后, 去掉重复的后剩下的个数
代码 :
#include <bits/stdc++.h>
using namespace std;
set<int> s[55];
int main() {
int n;
cin >> n;
int m, x, y;
for (int i = 1; i <= n; i++) {
cin >> m;
while (m--) {
cin >> x;
s[i].insert(x);
}
}
int k;
cin >> k;
while (k--) {
cin >> x >> y;
int len1 = s[x].size(), len2 = s[y].size();
int cnt = 0;
for (auto it : s[x]) {
if (s[y].find(it) != s[y].end()) cnt++;
}
printf("%.2lf%%\n", (cnt * 1.0 / (len1 + len2 - cnt)) * 100);
}
return 0;
}
7-5 悄悄关注
新浪微博上有个“悄悄关注”,一个用户悄悄关注的人,不出现在这个用户的关注列表上,但系统会推送其悄悄关注的人发表的微博给该用户。现在我们来做一回网络侦探,根据某人的关注列表和其对其他用户的点赞情况,扒出有可能被其悄悄关注的人。
输入格式:
输入首先在第一行给出某用户的关注列表,格式如下:
人数N 用户1 用户2 …… 用户N
其中N是不超过5000的正整数,每个用户i(i=1, ..., N)是被其关注的用户的ID,是长度为4位的由数字和英文字母组成的字符串,各项间以空格分隔。
之后给出该用户点赞的信息:首先给出一个不超过10000的正整数M,随后M行,每行给出一个被其点赞的用户ID和对该用户的点赞次数(不超过1000),以空格分隔。注意:用户ID是一个用户的唯一身份标识。题目保证在关注列表中没有重复用户,在点赞信息中也没有重复用户。
输出格式:
我们认为被该用户点赞次数大于其点赞平均数、且不在其关注列表上的人,很可能是其悄悄关注的人。根据这个假设,请你按用户ID字母序的升序输出可能是其悄悄关注的人,每行1个ID。如果其实并没有这样的人,则输出“Bing Mei You”。
输入样例1:
10 GAO3 Magi Zha1 Sen1 Quan FaMK LSum Eins FatM LLao
8
Magi 50
Pota 30
LLao 3
Ammy 48
Dave 15
GAO3 31
Zoro 1
Cath 60
输出样例1:
Ammy
Cath
Pota
输入样例2:
11 GAO3 Magi Zha1 Sen1 Quan FaMK LSum Eins FatM LLao Pota
7
Magi 50
Pota 30
LLao 48
Ammy 3
Dave 15
GAO3 31
Zoro 29
输出样例2:
Bing Mei You
代码 :
#include <bits/stdc++.h>
using namespace std;
map<string, bool> mp;
vector<pair<int, string>> v;
vector<string> ans;
int main() {
int n, m;
cin >> n;
string a;
for (int i = 0; i < n; i++) {
cin >> a;
mp[a] = 1; // 给关注列表里的 ID 做标记
}
cin >> m;
int sum = 0;
int x;
for (int i = 0; i < m; i++) {
cin >> a >> x;
sum += x;
v.push_back({x, a});
}
int ave = sum / m;
for (int i = 0; i < v.size(); i++) {
// 将点赞次数大于平均值 且 不在其关注列表的 ID 存入 ans
if (v[i].first > ave && !mp[v[i].second])
ans.push_back(v[i].second);
}
// 根据字典序排序
sort(ans.begin(), ans.end());
// ans 为空, 说明没有
if (ans.empty()) cout << "Bing Mei You" << endl;
else {
for (int i = 0; i < ans.size(); i++)
cout << ans[i] << endl;
}
return 0;
}
7-6 单身狗
“单身狗”是中文对于单身人士的一种爱称。本题请你从上万人的大型派对中找出落单的客人,以便给予特殊关爱。
输入格式:
输入第一行给出一个正整数 N(≤50000),是已知夫妻/伴侣的对数;随后 N 行,每行给出一对夫妻/伴侣——为方便起见,每人对应一个 ID 号,为 5 位数字(从 00000 到 99999),ID 间以空格分隔;之后给出一个正整数 M(≤10000),为参加派对的总人数;随后一行给出这 M 位客人的 ID,以空格分隔。题目保证无人重婚或脚踩两条船。
输出格式:
首先第一行输出落单客人的总人数;随后第二行按 ID 递增顺序列出落单的客人。ID 间用 1 个空格分隔,行的首尾不得有多余空格。
输入样例:
3
11111 22222
33333 44444
55555 66666
7
55555 44444 10000 88888 22222 11111 23333
输出样例:
5
10000 23333 44444 55555 88888
思路 : 先给出席的人都打上标记(
vis[i] = 1), 然后遍历 夫妻, 如果是两个人都到场了, 就解除标记 (vis[i] = 0); 最后遍历整个vis[], 被打上标记的就是落单的
代码 :
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int l[N], r[N]; // 存夫, 妻
bool vis[N];
vector<int> ans;
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) cin >> l[i] >> r[i];
int m;
cin >> m;
for (int i = 0; i < m; i++) {
int x;
cin >> x;
vis[x] = 1;
}
for (int i = 0; i < n; i++) {
int x = l[i], y = r[i];
// 如果 夫,妻 都到场了, 就解除标记
if (vis[x] && vis[y]) vis[x] = vis[y] = 0;
}
// 把标记了的存入 ans
for (int i = 0; i < N; i++) {
if (vis[i]) ans.push_back(i);
}
// 从小到大排序
sort(ans.begin(), ans.end());
cout << ans.size() << endl;
for (int i = 0; i < ans.size(); i++) {
if (i) printf(" %05d", ans[i]);
else printf("%05d", ans[i]);
}
return 0;
}
7-7 词典
你刚从滑铁卢搬到了一个大城市,这里的人们讲一种难以理解的外语方言。幸运的是,你有一本字典来帮助你理解它们。
输入格式:
输入第一行是正整数N和M,后面是N行字典条目(最多10000条),然后是M行要翻译的外语单词(最多10000个)。每一个字典条目都包含一个英语单词,后面跟着一个空格和一个外语单词。
输入中的每个单词都由最多10个小写字母组成。
输出格式:
输出翻译后的英文单词,每行一个单词。非词典中的外来词汇输出“eh”。
输入样例:
5 3
dog ogday
cat atcay
pig igpay
froot ootfray
loops oopslay
atcay
ittenkay
oopslay
输出样例:
cat
eh
loops
代码 :
#include <bits/stdc++.h>
using namespace std;
map<string, string> mp;
int main() {
int n, m;
cin >> n >> m;
string a, b;
while (n--) {
cin >> a >> b;
mp[b] = a;
}
while (m--) {
cin >> a;
if (mp[a] == "") cout << "eh" << endl;
else cout << mp[a] << endl;
}
return 0;
}
7-8 这是二叉搜索树吗?
一棵二叉搜索树可被递归地定义为具有下列性质的二叉树:对于任一结点,
- 其左子树中所有结点的键值小于该结点的键值;
- 其右子树中所有结点的键值大于等于该结点的键值;
- 其左右子树都是二叉搜索树。
所谓二叉搜索树的“镜像”,即将所有结点的左右子树对换位置后所得到的树。
给定一个整数键值序列,现请你编写程序,判断这是否是对一棵二叉搜索树或其镜像进行前序遍历的结果。
输入格式:
输入的第一行给出正整数 N(≤1000)。随后一行给出 N 个整数键值,其间以空格分隔。
输出格式:
如果输入序列是对一棵二叉搜索树或其镜像进行前序遍历的结果,则首先在一行中输出 YES ,然后在下一行输出该树后序遍历的结果。数字间有 1 个空格,一行的首尾不得有多余空格。若答案是否,则输出 NO。
输入样例 1:
7
8 6 5 7 10 8 11
输出样例 1:
YES
5 7 6 8 11 10 8
参考代码地址 :
---> 链接 <---
代码 :
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int a[N];
vector<int> v;
bool flag;
void f(int l, int r) {
if (l > r) return;
// l 是根节点, 所以 i 得是 l 的下一个
int i = l + 1, j = r;
if (!flag) {
// i 从左向右跑, 直到边界 或 a[i] 大于或等于 根节点
while (i <= r && a[i] < a[l]) i++;
// j 从右向左跑, 直到边界 或 a[j] 小于 根节点
while (j > l && a[j] >= a[l]) j--;
} else {
while (i <= r && a[i] >= a[l]) i++;
while (j > l && a[j] < a[l]) j--;
}
// 跑完之后 i 应该会在 j 的右边, 不符合条件就 return
if (i - j != 1) return;
// 继续向下 二分递归
f(l + 1, j);
f(i, r);
// 这里先递归遍历后再存, 就相当于 后序遍历
v.push_back(a[l]);
}
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
f(1, n);
// 如果不符合条件, 再跑一遍 镜像 的情况
if (v.size() != n) {
flag = 1;
v.clear();
f(1, n);
}
if (v.size() != n) cout << "NO" << endl;
else {
cout << "YES" << endl;
for (int i = 0; i < v.size(); i++) {
if (i) cout << " " << v[i];
else cout << v[i];
}
}
return 0;
}
7-9 二叉搜索树
对于一个无穷的满二叉排序树(如图),节点的编号是1,2,3,…。对于一棵树根为X的子树,沿着左节点一直往下到最后一层,可以获得该子树编号最小的节点;沿着右节点一直往下到最后一层,可以获得该子树编号最大的节点。现在给出的问题是“在一棵树根为X的子树中,节点的最小编号和最大编号是什么?”。请你给出答案。
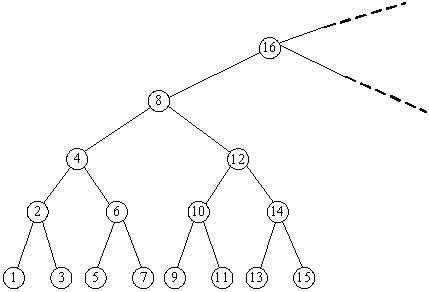
输入格式:
输入的第一行给出测试用例的数目,一个整数N。在后面的N行中,每行给出一个整数X(1<=X<=231-1),表示子树树根的编号。
输出格式:
输出N行,第i行给出第i个问题的答案。
输入样例:
2
8
10
输出样例:
1 15
9 11
思路 :
看图找规律, 如果把 数 都压到最底下看 就是1, 2, 3, 4, 5, 6, 7, 8, ...
对于给定x, 它和两边的数字差就是它到两边的宽度, 而 宽度 = 高度 - 1( 这里的高度是从叶子节点(高度为 1 )开始算的 ) ; 同时我们发现, 从左到右, 以 1 开始的一层 都能被 1 整除, 不能被 2 整除, 同样, 以 2 开始的一层的数, 都能被 2 整除, 但不能被 4 整除, 以此类推,,,,就能找到 x 所在的层数 ( 不确定这样找合不合理 )
代码 :
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
cin >> t;
while (t--) {
long long int x, y = 1;
cin >> x;
while (x % (y * 2) == 0) y *= 2;
y--;
cout << x - y << " " << x + y << endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号