PTA 21级数据结构与算法实验4—字符串和数组
7-1 字符串模式匹配(KMP)
给定一个字符串 text 和一个模式串 pattern,求 pattern 在text 中的出现次数。text 和 pattern 中的字符均为英语大写字母或小写字母。text中不同位置出现的pattern 可重叠。
输入格式:
输入共两行,分别是字符串text 和模式串pattern。
输出格式:
输出一个整数,表示 pattern 在 text 中的出现次数。
输入样例1:
zyzyzyz
zyz
输出样例1:
3
输入样例2:
AABAACAADAABAABA
AABA
输出样例2:
3
数据范围与提示:
1≤text, pattern 的长度 ≤106, text、pattern 仅包含大小写字母。
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int ne[N];
char s[N], p[N]; // s[] 是主串, p[] 是模式串
int main() {
scanf("%s %s", s + 1, p + 1); // 让字符串从下标 1 开始存
int n = strlen(s + 1), m = strlen(p + 1);
// 获取 ne[] 数组
int j = 0;
for (int i = 2; i <= m; i++) {
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j++;
ne[i] = j;
}
int ans = 0;
for (int i = 1, j = 0; i <= n; i++) {
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j++;
// 如果模式串匹配到最后, 记录后继续匹配
if (j == m) ans++, j = ne[j];
}
cout << ans << endl;
return 0;
}
7-2 【模板】KMP字符串匹配
给出两个字符串text和pattern,其中pattern为text的子串,求出pattern在text中所有出现的位置。
为了减少骗分的情况,接下来还要输出子串的前缀数组next。
输入格式:
第一行为一个字符串,即为text。
第二行为一个字符串,即为pattern。
输出格式:
若干行,每行包含一个整数,表示pattern在text中出现的位置。
接下来1行,包括length(pattern)个整数,表示前缀数组next[i]的值,数据间以一个空格分隔,行尾无多余空格。
输入样例:
ABABABC
ABA
输出样例:
1
3
0 0 1
样例说明:
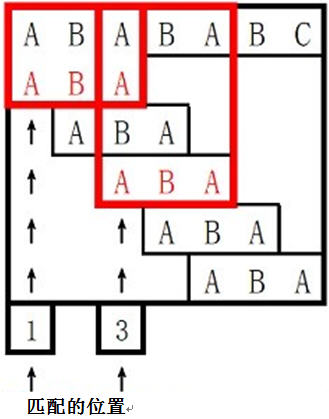
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int ne[N];
char s[N], p[N];
int main() {
scanf("%s %s", s + 1, p + 1);
int n = strlen(s + 1), m = strlen(p + 1);
int j = 0;
for (int i = 2; i <= m; i++) {
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j++;
ne[i] = j;
}
for (int i = 1, j = 0; i <= n; i++) {
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j++;
if (j == m) cout << i - m + 1 << endl, j = ne[j];
}
for (int i = 1; i <= m; i++) {
if (i == 1) cout << ne[i];
else cout << " " << ne[i];
}
return 0;
}
7-3 统计子串
编写算法,统计子串t在主串s中出现的次数。
输入格式:
首先输入一个整数T,表示测试数据的组数,然后是T组测试数据。每组测试数据在第一行中输入主串s,在第二行中输入子串t,s和t中不包含空格。
输出格式:
对于每组测试,若子串t在主串s中出现,则输出t在s中的子串位置和出现总次数,否则输出“0 0”。引号不必输出。
输入样例:
2
abbbbcdebb
bb
abcde
bb
输出样例:
2 4
0 0
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int ne[N];
char s[N], p[N];
int main() {
int t;
cin >> t;
while (t--) {
scanf("%s %s", s + 1, p + 1);
int n = strlen(s + 1), m = strlen(p + 1);
int j = 0;
memset(ne, 0, sizeof(ne));
for (int i = 2; i <= m; i++) {
if (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j++;
ne[i] = j;
}
int cnt = 0;
bool flag = 0;
int num = 0;
for (int i = 1, j = 0; i <= n; i++) {
if (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j++;
if (j == m) {
cnt++, j = ne[j];
// 记录第一次匹配的位置
if (!flag) flag = 1, num = i - m + 1;
}
}
if (cnt) cout << num << " " << cnt << endl;
else cout << "0 0" << endl;
}
return 0;
}
7-4 好中缀
我们称一个字符串S的子串T为好中缀,如果T是去除S中满足如下条件的两个子串p和q后剩余的字符串。
(1)p是S的前缀,q是S的后缀;
(2)p=q;
(3)p和q是满足条件(1)(2)的所有子串中的第二长者。
注意一个字符串不能称为自己的前缀或后缀。好中缀至少为空串,其长度大于等于0,不能为负数。
输入格式:
输入为一个字符串S,包含不超过100000个字母。
输出格式:
输出为一个整数,表示好中缀的长度。
输入样例1:
abcabcxxxabcabc
输出样例1:
9
输入样例2:
xacbacba
输出样例2:
8
输入样例3:
aaa
输出样例3:
1
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int ne[N];
char p[N];
int main() {
scanf("%s", p + 1);
int m = strlen(p + 1);
int j = 0;
for (int i = 2; i <= m; i++) {
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j++;
ne[i] = j;
}
int ans = m - 2 * ne[ne[m]];
if (ans <= 0) cout << "0" << endl;
else cout << ans << endl;
return 0;
}
7-5 病毒变种
病毒DNA可以表示成由一些字母组成的字符串序列,且病毒的DNA序列是环状的。例如,假设病毒的DNA序列为baa,则该病毒的DNA序列有三种变种:baa,aab,aba。试编写一程序,对给定的病毒DNA序列,输出该病毒所有可能的DNA序列(假设变种不会重复)。
输入格式:
输入第一行中给出1个整数i(1≤i≤11),表示待检测的病毒DNA。 输入i行串序列,每行一个字符串,代表病毒的DNA序列,病毒的DNA序列长度不超过500。
输出格式:
依次逐行输出每个病毒DNA所有变种,各变种之间用空格分隔。
输入样例1:
1
baa
输出样例1:
baa aab aba
输入样例2:
2
abc
baac
输出样例2:
abc bca cab
baac aacb acba cbaa
代码
C++
#include<bits/stdc++.h>
using namespace std;
int main() {
int t;
cin >> t;
while (t--) {
string a;
cin >> a;
int len = a.size();
for (int i = 0 ; i < len; i++) {
string x = a.substr(0, i);
string y = a.substr(i);
cout << y << x << " ";
}
cout << endl;
}
return 0;
}
C语言
#include <bits/stdc++.h>
using namespace std;
char a[510];
int main() {
int t;
scanf("%d", &t);
while (t--) {
scanf("%s", a);
int len = strlen(a);
for (int i = 0; i < len; i++) {
for (int j = i; j < len; j++) printf("%c", a[j]);
for (int j = 0; j < i; j++) printf("%c", a[j]);
printf(" ");
}
printf("\n");
}
return 0;
}
7-6 判断对称矩阵
将矩阵的行列互换得到的新矩阵称为转置矩阵。
把 m × n 矩阵的行列互换之后得到的矩阵,称为 A 的转置矩阵,记作 AT
由定义可知, A 为m×n 矩阵,则 AT为 n×m 矩阵。
n×n矩阵称之为 n阶方阵
如果 n 阶方阵和它的转置相等,即 AT= A ,则称矩阵 A 为对称矩阵。
输入格式:
在第一行内给出n值(1<n<100)。
从第二行以后给出n阶矩阵所有行的元素值。
输出格式:
当输入的n阶矩阵是对称矩阵,输出“Yes”,否则输出“No”。
输入样例1:
3
1 0 2
-2 1 3
4 3 2
输出样例1:
No
输入样例2:
3
1 -2 4
-2 1 3
4 3 2
输出样例2:
Yes
代码
#include<bits/stdc++.h>
using namespace std;
int a[111][111];
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> a[i][j];
}
}
bool flag = 1;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (a[i][j] != a[j][i]) {
flag = 0;
break;
}
}
if (!flag) break;
}
if (flag) cout << "Yes" << endl;
else cout << "No" << endl;
return 0;
}
7-7 三元组顺序表表示的稀疏矩阵转置运算Ⅰ
三元组顺序表表示的稀疏矩阵转置。
输入格式:
输入第1行为矩阵行数m、列数n及非零元素个数t。
按行优先顺序依次输入t行,每行3个数,分别表示非零元素的行标、列标和值。
输出格式:
输出转置后的三元组顺序表结果,每行输出非零元素的行标、列标和值,行标、列标和值之间用空格分隔,共t行。
输入样例:
3 4 3
0 1 -5
1 0 1
2 2 2
输出样例:
0 1 1
1 0 -5
2 2 2
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
struct node {
int x, y, w;
}p[N];
bool cmp(node x, node y) {
if (x.x != y.x) return x.x < y.x;
return x.y < y.y;
}
int main() {
int n, m, t;
cin >> n >> m >> t;
// 直接 x 和 y 交换输入, 相当于转置后了
for (int i = 0; i < t; i++) cin >> p[i].y >> p[i].x >> p[i].w;
sort(p, p + t, cmp);
for (int i = 0; i < t; i++) cout << p[i].x << " " << p[i].y << " " << p[i].w << endl;
return 0;
}
7-8 三元组顺序表表示的稀疏矩阵加法
三元组顺序表表示的稀疏矩阵加法。
输入格式:
输入第1行为两个同型矩阵的行数m、列数n,矩阵A的非零元素个数t1,矩阵B的非零元素个数t2。
按行优先顺序依次输入矩阵A三元组数据,共t1行,每行3个数,分别表示非零元素的行标、列标和值。
按行优先顺序依次输入矩阵B三元组数据,共t2行,每行3个数,分别表示非零元素的行标、列标和值。
输出格式:
输出第1行为相加后矩阵行数m、列数n及非零元素个数t。
输出t行相加后的三元组顺序表结果,每行输出非零元素的行标、列标和值,每行数据之间用空格分隔。
输入样例:
4 4 3 4
0 1 -5
1 3 1
2 2 1
0 1 3
1 3 -1
3 0 5
3 3 7
输出样例:
4 4 4
0 1 -2
2 2 1
3 0 5
3 3 7
代码
#include<bits/stdc++.h>
using namespace std;
map<pair<int, int>, int> mp;
int main() {
int n, m, t1, t2;
cin >> n >> m >> t1 >> t2;
int x, y, w;
for (int i = 0; i < t1; i++) {
cin >> x >> y >> w;
mp[{x, y}] += w;
}
for (int i = 0; i < t2; i++) {
cin >> x >> y >> w;
mp[{x, y}] += w;
}
int cnt = 0;
for (auto it : mp) {
if (it.second) cnt++;
}
cout << n << " " << m << " " << cnt << endl;
for (auto it : mp) {
if (it.second) cout << it.first.first << " " << it.first.second << " " << it.second << endl;
}
return 0;
}
7-9 三元组顺序表表示的稀疏矩阵转置Ⅱ
三元组顺序表表示的稀疏矩阵转置Ⅱ。设a和b为三元组顺序表变量,分别表示矩阵M和T。要求按照a中三元组的次序进行转置,并将转置后的三元组置入b中恰当的位置。
输入格式:
输入第1行为矩阵行数m、列数n及非零元素个数t。
按行优先顺序依次输入t行,每行3个数,分别表示非零元素的行标、列标和值。
输出格式:
按置入b中的顺序输出置入的位置下标,转置后的三元组行标、列标和值,数据之间用空格分隔,共t行。
输入样例:
3 4 3
0 1 -5
1 0 1
2 2 2
输出样例:
1 1 0 -5
0 0 1 1
2 2 2 2
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
struct node {
int x, y, w;
} p[N];
map<pair<int, int>, int> mp;
vector<node> v;
bool cmp(node a, node b) {
if (a.x != b.x) return a.x < b.x;
return a.y < b.y;
}
int main() {
int n, m, t;
cin >> n >> m >> t;
for (int i = 0; i < t; i++) cin >> p[i].y >> p[i].x >> p[i].w;
for (int i = 0; i < t; i++) v.push_back({p[i].x, p[i].y});
sort(v.begin(), v.end(), cmp);
for (int i = 0; i < t; i++) mp[{v[i].x, v[i].y}] = i;
for (int i = 0; i < t; i++) {
int x = p[i].x, y = p[i].y, w = p[i].w;
cout << mp[{x, y}] << " " << x << " " << y << " " << w << endl;
}
return 0;
}
7-10 最大子矩阵和问题
最大子矩阵和问题。给定m行n列的整数矩阵A,求矩阵A的一个子矩阵,使其元素之和最大。
输入格式:
第一行输入矩阵行数m和列数n(1≤m≤100,1≤n≤100),再依次输入m×n个整数。
输出格式:
输出第一行为最大子矩阵各元素之和,第二行为子矩阵在整个矩阵中行序号范围与列序号范围。
输入样例:
5 6
60 3 -65 -92 32 -70
-41 14 -38 54 2 29
69 88 54 -77 -46 -49
97 -32 44 29 60 64
49 -48 -96 59 -52 25
输出样例:
输出第一行321表示子矩阵各元素之和,输出第二行2 4 1 6表示子矩阵的行序号从2到4,列序号从1到6
321
2 4 1 6
代码
#include <bits/stdc++.h>
using namespace std;
// 题目给 100, 但实际得开 1e3 才能过
const int N = 1e3 + 10;
int a[N][N];
int d[N][N];
int t[N];
int x, y, xx, yy;
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
scanf("%d", &a[i][j]);
d[i][j] = d[i - 1][j] + a[i][j];
}
}
int Max = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j <= n; j++) {
for (int k = 1; k <= m; k++) t[k] = d[j][k] - d[i][k];
int sum = 0;
int l = 1, r = 1;
for (int k = 1; k <= m; k++) {
sum += t[k];
if (sum < 0) {
sum = t[k];
l = r = k;
} else {
r = k;
}
if (sum > Max) {
Max = sum;
x = i + 1;
y = l;
xx = j;
yy = r;
}
}
}
}
printf("%d\n", Max);
printf("%d %d %d %d\n", x, xx, y, yy);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号