Codeforces Round #236 (Div. 2)E. Strictly Positive Matrix(402E)
You have matrix a of size n × n. Let's number the rows of the matrix from 1 to n from top to bottom, let's number the columns from 1 ton from left to right. Let's use aij to represent the element on the intersection of the i-th row and the j-th column.
Matrix a meets the following two conditions:
- for any numbers i, j (1 ≤ i, j ≤ n) the following inequality holds: aij ≥ 0;
![]() .
.
Matrix b is strictly positive, if for any numbers i, j (1 ≤ i, j ≤ n) the inequality bij > 0 holds. You task is to determine if there is such integer k ≥ 1, that matrix ak is strictly positive.
The first line contains integer n (2 ≤ n ≤ 2000) — the number of rows and columns in matrix a.
The next n lines contain the description of the rows of matrix a. The i-th line contains n non-negative integers ai1, ai2, ..., ain (0 ≤ aij ≤ 50). It is guaranteed that 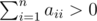 .
.
If there is a positive integer k ≥ 1, such that matrix ak is strictly positive, print "YES" (without the quotes). Otherwise, print "NO" (without the quotes).
2
1 0
0 1
NO
5
4 5 6 1 2
1 2 3 4 5
6 4 1 2 4
1 1 1 1 1
4 4 4 4 4
YES
题意: 矩阵matrix[n][n], 对角线上元素不全为0, 其他元素的值大于等于0. 问是否存在k 使得 矩阵的k次幂之后 元素的值全部大于0.
设 A = B2 , B 为一邻接矩阵, 则A[i][j] 的实际意义为 从i到j 经过一个点(不包含i, j)的路径的个数。。。对于k次幂就是经过k-1个点的路径的个数了。
要使 A[i][j] 大于0 ,(有向图) i 到j必须连通。。 A[j][i] > 0 && A[i][j] < 0 ,则i, j之间必能形成回路。
可以理解为 从任意点开始都可以遍历整个有向图。
建两个图(正向 反向),分别跑dfs。。判断一下即可。
1 #include <bits/stdc++.h> 2 using namespace std; 3 vector<int>G1[2015]; 4 vector<int>G2[2015]; 5 int c1, c2; 6 bool vis[2015]; 7 void dfs1(int r) 8 { 9 c1++; 10 vis[r] = true; 11 for (int i = 0; i < G1[r].size(); i++) 12 { 13 if (!vis[G1[r][i]]) 14 dfs1(G1[r][i]); 15 } 16 } 17 void dfs2(int r) 18 { 19 c2++; 20 vis[r] = true; 21 for (int i = 0; i < G2[r].size(); i++) 22 { 23 if (!vis[G2[r][i]]) 24 dfs2(G2[r][i]); 25 } 26 } 27 int main() 28 { 29 #ifndef ONLINE_JUDGE 30 freopen("in.txt","r",stdin); 31 #endif 32 int n; 33 while (~scanf ("%d", &n)) 34 { 35 for (int i = 0; i <= n; i++) 36 { 37 G1[i].clear(); 38 G2[i].clear(); 39 } 40 for (int i = 0; i < n; i++) 41 { 42 for (int j = 0; j < n; j++) 43 { 44 int x; 45 scanf ("%d", &x); 46 if (i != j && x) 47 { 48 G1[i+1].push_back(j+1); 49 G2[j+1].push_back(i+1); 50 } 51 } 52 } 53 c1 = c2 = 0; 54 memset(vis, false, sizeof(vis)); 55 dfs1(1); 56 memset(vis, false, sizeof(vis)); 57 dfs2(1); 58 printf("%s\n", (c1 == n && c2 == n) ? "YES" : "NO"); 59 } 60 return 0; 61 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号