2.（图）-深度优先遍历DFS

        从图的某个节点开始遍历，访问了则标记下来，然后访问此点所有邻域中任意点为新起点，且做上访问标记，通常通过递归和栈的技巧实现。

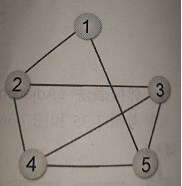
1：以1为起点，[5,2]入栈

2：弹出上面的2,2相邻且未标记访问的3,4入栈[5,4,3]

3：弹3,入4,5;[5,4,5,4]

4：弹4，入5；[5,4,5,5]

5：弹5,剩余[5,4,5]

6：[5,4,5]均被标记访问，依次弹出，不打印、访问节点

最终深度优先遍历依次访问节点:1,2,3,4,5

1.基于递归

class list_node:
    def __init__(self):
        self.val = 0
        self.next = None


def dfs(current, run=[0] * 9):
    '''
    基于递归实现
    :param current:
    :param run:
    :return:
    '''
    run[current] = 1
    print('[%d]' % current, end=' ')
    ptr = head[current].next
    while ptr != None:  # 遍历所有current节点连接的节点
        if run[ptr.val] == 0:  # 连接点未访问
            dfs(ptr.val, run)
        ptr = ptr.next



def graph_create(data):
    '''
    创建链表表示图
    :return:
    '''
    global head
    for i in range(len(head)):
        head[i] = list_node()
        head[i].val = i
        head[i].next = None
        ptr = head[i]
        for j in range(len(data)):
            if data[j][0] == i:
                newnode = list_node()
                newnode.val = data[j][1]
                newnode.next = None
                ptr.next = newnode
                ptr = ptr.next


def print_head(head):
    '''
    打印函数
    :return:
    '''
    for i in range(len(head)):
        ptr = head[i]
        print('顶点%d=>' % i, end=' ')
        ptr = ptr.next
        while ptr != None:
            print('[%d] ' % ptr.val, end=' ')
            ptr = ptr.next
        print()


data = [[1, 2], [2, 1], [1, 3], [3, 1],
        [2, 4], [4, 2], [2, 5], [5, 2],
        [3, 6], [6, 3], [3, 7], [7, 3],
        [4, 8], [8, 4], [5, 8], [8, 5],
        [6, 8], [8, 6], [8, 7], [7, 8]]

head = [None] * 9
graph_create(data)
print_head(head)
print('1节点开始，递归深度优先遍历：')
dfs(1)
print()

2.基于栈 

def dfs_stack(current):
    '''
    基于栈
    :param current:
    :return:
    '''
    node_stack = []
    if len(node_stack) == 0:
        node_stack.append(current)
    run = [0] * 9
    while len(node_stack) != 0:
        out = node_stack.pop()
        if run[out] == 0:
            print('[%d]' % out, end=' ')
            run[out] = 1
        ptr = head[out].next
        while ptr != None:  # 遍历所有current节点连接的节点
            if run[ptr.val] == 0:  # 连接点未访问
                node_stack.append(ptr.val)
            ptr = ptr.next

run = [0] * 9
print('1节点开始，栈深度优先遍历：')
dfs_stack(1)

 

output：

顶点0=> 
顶点1=> [2]  [3]  
顶点2=> [1]  [4]  [5]  
顶点3=> [1]  [6]  [7]  
顶点4=> [2]  [8]  
顶点5=> [2]  [8]  
顶点6=> [3]  [8]  
顶点7=> [3]  [8]  
顶点8=> [4]  [5]  [6]  [7]  
1节点开始，递归深度优先遍历：
[1] [2] [4] [8] [5] [6] [3] [7] 
1节点开始，栈深度优先遍历：
[1] [3] [7] [8] [6] [5] [2] [4]