《最优化导论》-10共轭方向法
1.共轭方向法
效率位于最速下降和牛顿法之间,优点:

1.1共轭:
关于对称实矩阵Q共轭

关于对称正定矩阵Q共轭

1.2基本共轭方向算法流程:
n步之内收敛到全局极小点,证明:10.1

1.3共轭方向的迭代,每次ak都是最佳步长:
![]()

2.共轭梯度法
不需要先给定共轭方向,而是根据迭代不断产生
![]()


2.1共轭梯度的3种修正
共轭梯度每次都要计算黑塞矩阵,计算量较大,有一些修正可以避免计算,ak可以用一维搜索替代得到,所以修正Bk。
1)Hestenes-Stiefel修正
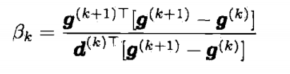
2)Polak-Ribiere修正

3)Fletcher-Reeves修正

问题:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号