ML-线性回归-公式推导- 多种实现

1. 简单线性回归

只有一个未知数x，两个 $\Theta$ 参数的，称为简单线性回归，一条直线。此时不需要线性代数概念，直接迭代求解，形如：

1.1 表示形式

1.2 定义损失

1.3 求参，极大似然

2.多元线性回归

2.1形式

2.2误差

2.3求参

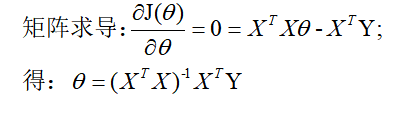
2.4问题

$X^{T}X$ 通常不是nxn矩阵，既，数据量：行n，自变量及偏置：列p+1，通常n!=p+1，也就是说矩阵 $X^{T}X$ 不存在逆；

可以：1)加入单位矩阵，让其变正定；其中 $\lambda$ 要足够大使得括号内矩阵可逆。

2）可以通过一些其它随机优化器算法寻找参数。

3 实现

3.1 最小二乘法、带正则化、基于scipy优化器实现：https://blog.csdn.net/jiang425776024/article/details/86801232

3.2 sklearn库的实现

1）LinearRegression：https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html

我们平时说的最常见普通的线性回归，它的损失函数也是最简单的，如下：

　　　　 $J(\mathbf\theta) = \frac{1}{2}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y})$

对于这个损失函数，一般有梯度下降法和最小二乘法两种极小化损失函数的优化方法，而scikit中的LinearRegression类用的是最小二乘法。通过最小二乘法，可以解出线性回归系数θθ为：

　　　　 $\mathbf{\theta} = (\mathbf{X^{T}X})^{-1}\mathbf{X^{T}Y}$

使用场景：一般来说，只要我们觉得数据有线性关系，LinearRegression类是我们的首先。如果发现拟合或者预测的不好，再考虑用其他的线性回归库。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.linear_model import LinearRegression

'''
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression
使用场景：一般来说，只要我们觉得数据有线性关系，LinearRegression类是我们的首先。如果发现拟合或者预测的不好，再考虑用其他的线性回归库。
'''
fig = plt.figure()
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
ax = Axes3D(fig)

# 构造X数据
X = np.random.randint(0, 7, (20, 2))
# 构造y数据， y = 1 * x_0 + 2 * x_1 + 3，后面打印参数会发现，是一致的
y = np.dot(X, np.array([1, 2])) + 3
# 绘制原始数据
ax.scatter(X[:, 0], X[:, 1], y, marker='o')

# 参数打印
reg = LinearRegression().fit(X, y)
print('分数：', reg.score(X, y))
print('参数：', reg.coef_)
print('截距：', reg.intercept_)

# 测试数据生成
test_x0 = np.linspace(0, 5, 10)
test_x1 = np.linspace(0, 5, 10)
test_X = np.array([test_x0, test_x1]).T

pred_y = reg.predict(test_X)
print('预测：', pred_y)

# 生成预测图形
ax.plot(test_X[:, 0], test_X[:, 1], pred_y, c='r')
plt.show()

2.Ridge/RidgeCV岭回归/L2正则化：https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.RidgeCV.html#sklearn.linear_model.RidgeCV

使用场景：一般来说，只要我们觉得数据有线性关系，用LinearRegression类拟合的不是特别好，需要正则化，可以考虑用RidgeCV类。如果输入特征的维度很高，而且是稀疏线性关系的话，RidgeCV类就不合适了。
这时应该主要考虑下面Lasso回归类家族。

其思想是对损失函数加入正则化：

$J(\mathbf\theta) = \frac{1}{2}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y}) + \frac{1}{2}\alpha||\theta||_2^2$

使得系数求解变为：

$\mathbf{\theta = (X^TX + \alpha E)^{-1}X^TY}$

其中额外参数a，在sklearn中，Ridge类并没有用到交叉验证之类的验证方法，RidgeCV类的损失函数和损失函数的优化方法完全与Ridge类相同，区别在于验证方法:alphas=[0.1, 1.0, 10.0,...],RidgeCV可以传入多个参数，自动帮你选择最佳的。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.linear_model import RidgeCV


fig = plt.figure()
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
ax = Axes3D(fig)

# 构造X数据
X = np.random.randint(0, 7, (20, 2))
# 构造y数据， y = 1 * x_0 + 2 * x_1 + 3，后面打印参数会发现，是一致的
y = np.dot(X, np.array([1, 2])) + 3
# 绘制原始数据
ax.scatter(X[:, 0], X[:, 1], y, marker='o')

# 参数打印
reg = RidgeCV(alphas=[0.1, 1.0, 10.0]).fit(X, y)
print('分数：', reg.score(X, y))
print('参数：', reg.coef_)
print('截距：', reg.intercept_)

# 测试数据生成
test_x0 = np.linspace(0, 5, 10)
test_x1 = np.linspace(0, 5, 10)
test_X = np.array([test_x0, test_x1]).T

pred_y = reg.predict(test_X)
print('预测：', pred_y)

# 生成预测图形
ax.plot(test_X[:, 0], test_X[:, 1], pred_y, c='r')
plt.show()

#
分数： 0.9999988863966677
参数： [0.99947475 1.9975713 ]
截距： 3.009245913853947
预测： [ 3.00924591  4.6742715   6.33929708  8.00432266  9.66934824 11.33437383
 12.99939941 14.66442499 16.32945058 17.99447616]

3.Lasso/LassoCV/L1正则化:https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LassoCV.html#sklearn.linear_model.LassoCV

$J(\mathbf\theta) = \frac{1}{2m}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y}) + \alpha||\theta||_1$

Lasso回归可以使得一些特征的系数变小，甚至还是一些绝对值较小的系数直接变为0。增强模型的泛化能力。

损失函数的优化方法：

Lasso回归的损失函数优化方法常用的有两种，坐标轴下降法和最小角回归法。Lasso类采用的是坐标轴下降法，后面讲到的LassoLars类采用的是最小角回归法

使用场景：

一般来说，对于高维的特征数据，尤其线性关系是稀疏的，我们会采用Lasso回归。或者是要在一堆特征里面找出主要的特征，那么Lasso回归更是首选了。但是Lasso类需要自己对α调优，所以不是Lasso回归的首选，一般用到的是下一节要讲的LassoCV类，可以自动帮你选择，或者你提供一组alphas数据让它选择。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.linear_model import LassoCV

fig = plt.figure()
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
ax = Axes3D(fig)

# 构造X数据
X = np.random.randint(0, 7, (20, 2))
# 构造y数据， y = 1 * x_0 + 2 * x_1 + 3，后面打印参数会发现，是一致的
y = np.dot(X, np.array([1, 2])) + 3
# 绘制原始数据
ax.scatter(X[:, 0], X[:, 1], y, marker='o')

# 参数打印
reg = LassoCV(alphas=[0.1, 1.0, 10.0]).fit(X, y)
print('分数：', reg.score(X, y))
print('参数：', reg.coef_)
print('截距：', reg.intercept_)

# 测试数据生成
test_x0 = np.linspace(0, 5, 10)
test_x1 = np.linspace(0, 5, 10)
test_X = np.array([test_x0, test_x1]).T

pred_y = reg.predict(test_X)
print('预测：', pred_y)

# 生成预测图形
ax.plot(test_X[:, 0], test_X[:, 1], pred_y, c='r')
plt.show()
#
分数： 0.9998181323039398
参数： [0.97476331 1.98150169]
截距： 3.109000578571484
预测： [ 3.10900058  4.75137002  6.39373947  8.03610891  9.67847836 11.3208478
 12.96321725 14.60558669 16.24795614 17.89032558]

还有许多其它类型的回归介绍：https://www.cnblogs.com/pinard/p/6026343.html

官方文档关于线性模型的使用说明：https://scikit-learn.org/stable/modules/classes.html#module-sklearn.linear_model

其使用方法和上面一致，这一点在sklearn库中很好。

posted @ 2019-02-19 09:37 jj千寻阅读(321) 评论(0) 编辑收藏举报

刷新页面返回顶部

425776024

ML-线性回归-公式推导- 多种实现

1. 简单线性回归

2.多元线性回归

公告