ML-逻辑回归的公式推导及实现、LogisticRegression， LogisticRegressionCV 和logistic_regression_path
目录
1.简介
逻辑回归并不是回归，是分类算法。通过函数映射，通常映射后的值＞0.5称为正例，反之反例，这样的学习称为二分类。
2.数学背景
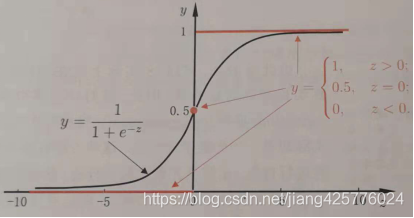
定义映射函数：
求导性质：
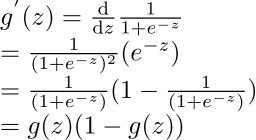
3.推导
令z表示线性关系：
其中x是给定的数据，b是偏置，
是需要学习到的参数，通过这样映射得到y∈[0,1]，记y为正例概率，1-y则是反例概率.
则：
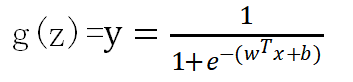
记为概率形式,p1,p0有：
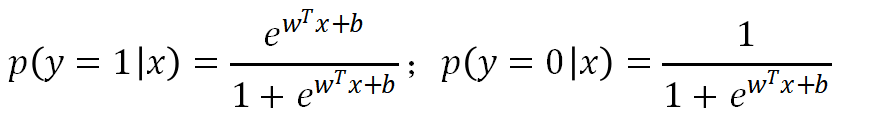
对正反比取对数发现：
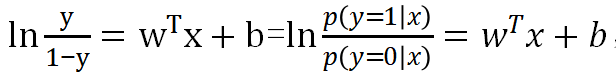
结果就是z，也就是说z越大，正概率比反概率的比越大，越可能是正。这样的一个模型具有分类表示能力。
4.联合概率
记
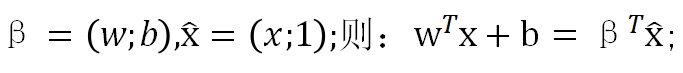
联合0、1概率可写在一起，为：
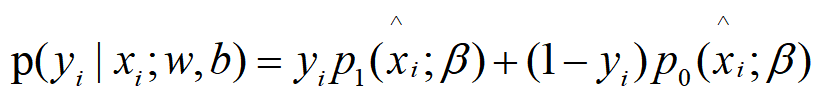
取对数时：
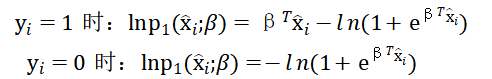
所以对数联合概率记为：
5.求参、极大似然
极大似然估计w,b的值，记m个样本的联合模型：
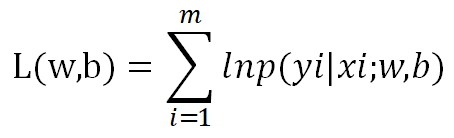
极大化
等价于极小化：
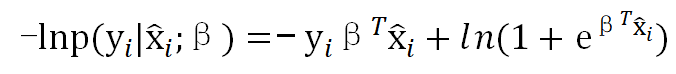
最终，转为对m个数据集D求极小化：
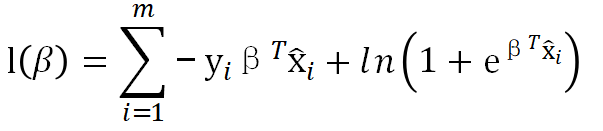
6.参数求解：
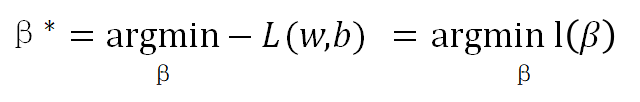
求得参数后，就可以利用：
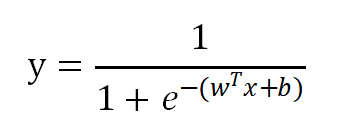
进行预测了，当y>0.5的时候意味着正的可能性比反的可能性大，既被预测为正例。
7.牛顿法、拟牛顿法、梯度下降法等求参：
1）牛顿法：https://blog.csdn.net/jiang425776024/article/details/87601854
2）拟牛顿法：https://blog.csdn.net/jiang425776024/article/details/87602847
3）梯度下降：https://blog.csdn.net/jiang425776024/article/details/87601506
牛顿法：
方便起见，在这里需要求的是参数w,b的整体
，根据 5 中的损失函数：
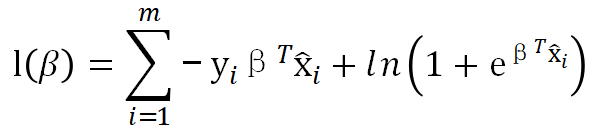
一阶导数为：
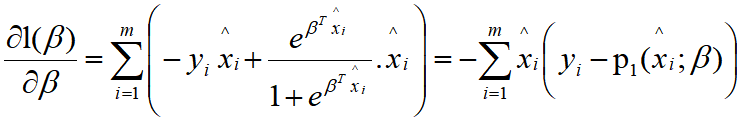
根据 2 中
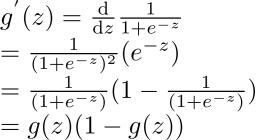
因为
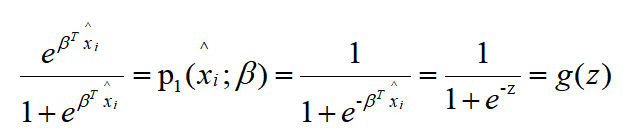
所以，二阶导数为：
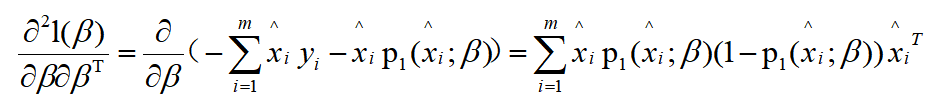
因此，牛顿法参数的迭代形式：
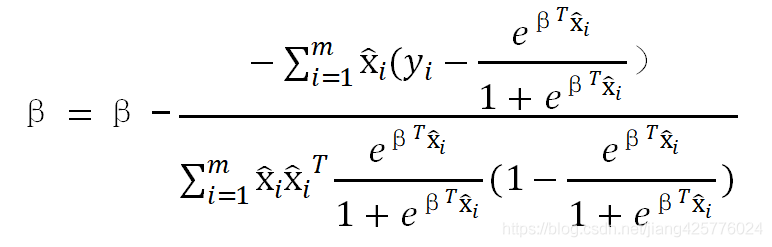
当然，牛顿法也可以加上一维线性搜索（https://blog.csdn.net/jiang425776024/article/details/87600422），即，如下梯度法那样，在上面的导数式子上，加上学习率a。
梯度下降法
只需要一阶导数，a为步长，一般∈[0,1]，代入上面的 1 阶导数即可：
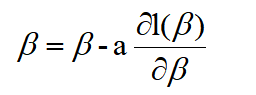
需要说明的是，牛顿法用到了二阶导数的信息，所以通常上，牛顿法的效率总是比梯度下降法好。
8.完整流程
输入：
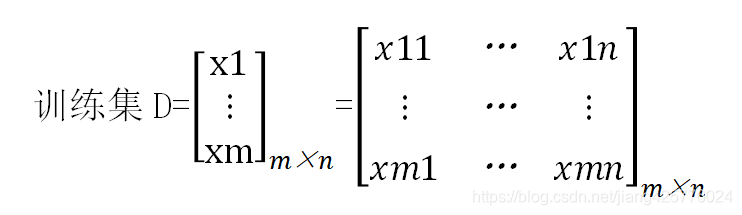
过程：随机初始化参数Beita
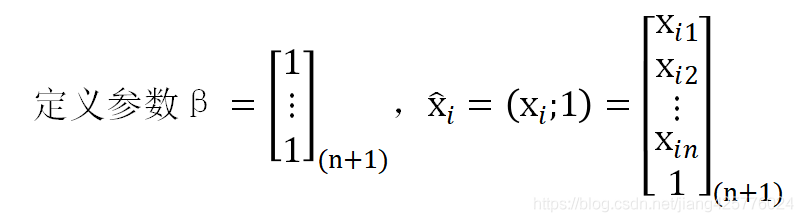
while 
总体变化量<某个阀值：对进行7中那样的迭代更新
9.正则化
和其它算法一样，可以对参数进行正则化，L1\L2等，通常都是在损失函数后面加上形如L2正则化：，其中a为正则化强度，theta为模型参数。这时参数更新需要加入对正则化这部分的求导。
10.多元逻辑回归
二分类中，形如：
多分类中假设有K>2个类别，则有K-1个方程：
、
,...,
则K元逻辑回归的概率分布如下：
，k = 1,2,...K-1
剩下的多元逻辑回归的损失函数推导以及优化方法和二元逻辑回归类似。
还有一种简单粗暴的办法就是，构造多个二分类，比如有A，B,C,D 四个类，那么按照上面的，可以构造4个二分类：正A与反(B，C,D);正B与反(A,C,D)，.....。这样，就可以按照二分类的情况进行多分类了，只是判断的时候需要进行多个if判断。
11.scikit-learn中逻辑回归
主要是3个：LogisticRegression， LogisticRegressionCV 和logistic_regression_path。
其中LogisticRegression和 LogisticRegressionCV的主要区别是 LogisticRegressionCV使用了交叉验证来选择（9中正则化介绍的a）正则化系数C，而LogisticRegression需要自己每次指定一个正则化系数。
logistic_regression_path主要用在模型选择，不能直接来做预测，只能选择合适逻辑回归的系数和正则化系数。
使用：
这里不会详细介绍api的参数，点击可查看LogisticRegression， LogisticRegressionCV的参数说明，
或者：https://www.cnblogs.com/pinard/p/6035872.html。
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.linear_model import LogisticRegressionCV
'''
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegressionCV.html#sklearn.linear_model.LogisticRegressionCV
'''
X, y = load_iris(return_X_y=True)
#solver='lbfgs'使用拟牛顿法迭代寻参
#random_state=0随机种子，这个很必要，数值随便
'''
multi_class参数决定了我们分类方式的选择，有 ovr和multinomial两个值可以选择，默认是 ovr。
ovr即前面提到的one-vs-rest(OvR)，而multinomial即前面提到的many-vs-many(MvM)。如果是二元逻辑回归，ovr和multinomial并没有任何区别，区别主要在多元逻辑回归上。
'''
clf = LogisticRegression(random_state=0, C=2, solver='lbfgs', multi_class='multinomial').fit(X, y)#指定了正则化强度为2
clfcv = LogisticRegressionCV(random_state=0, solver='lbfgs', multi_class='multinomial').fit(X, y)#cv类自动寻找正则化强度
pd = clf.predict(X[:2, :])
pdcv = clf.predict(X[:2, :])
print(X[:2, :], '预测类型：', pd)
print(X[:2, :], '预测类型：', pdcv)
pbd = clf.predict_proba(X[:2, :])
pbdcv = clf.predict_proba(X[:2, :])
print(X[:2, :], '预测类型的概率：', pbd)
print(X[:2, :], '预测类型的概率：', pbdcv)
print('预测分数：', clf.score(X, y))
print('预测分数：', clfcv.score(X, y))
'''
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]] 预测类型： [0 0]
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]] 预测类型： [0 0]
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]] 预测类型的概率： [[9.89252266e-01 1.07477333e-02 2.22652613e-10]
[9.82191282e-01 1.78087169e-02 6.46675701e-10]]
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]] 预测类型的概率： [[9.89252266e-01 1.07477333e-02 2.22652613e-10]
[9.82191282e-01 1.78087169e-02 6.46675701e-10]]
预测分数： 0.9866666666666667
预测分数： 0.98
Process finished with exit code 0
'''
