《最优化导论》-23有约束优化的求解算法

1.形式

2.投影法

通常迭代形如：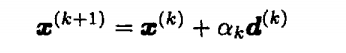

2.1当有约束时，这类算法迭代出的点很可能不满足约束，可以使用投影形式，然点投影到约束内，u,l为约束范围：

这样对上面的迭代形式进行改进，然每次迭代后的点保持在约束内：

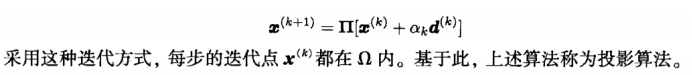
2.2投影梯度法

 

3.线性约束优化的投影

3.1 投影算子P

线性约束时，投影算子是正交投影矩阵P:

存在约束时，负梯度方向并不一定就是可行方向，因此可以借助投影矩阵P，得到迭代形式：

3.2投影时的极小点条件

原先无约束时是梯度为0：

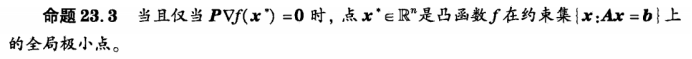
4.拉格朗日法

4.1 仅含等式约束时，拉格朗日法迭代更新：

4.2 含不等式约束时，拉格朗日法迭代更新：

5.罚函数法

1）对于约束问题，转化为无约束问题，其中会加一个惩罚项，惩罚大小与超出约束正相关。

2）定义

3）绝对值罚函数

4）分析