ML决策树ID3、C4.5、CART公式推导实现
目录
1.决策树
1.1定义
Ck表示第k个类,特征T可取n个不同的值;数据集D将T相同的特征取值划分为一个集合,共划分n个不同子集{D1,D2,...Dn}
输入:训练集D,特征集A,最小信息增益阀值e
输出:决策树T
2.ID3算法
ID3基于信息增益
1)定义Ent:信息熵,D内类越乱越大,D内类一致时为0

2)定义Gain(D,a):信息增益,描述的是D依据属性来划分所能够获得的“纯度提升”:尽可能快的让分下去的数据类别越来越一致

3)流程:
ThreeGenerate(D,A):

每次对输入的数据集D划分依据a*属性做划分,

实际中不可能一直细分,那样太慢或过拟合,增益小于某个阀值时就直接标记为节点中数据集最大类:

遍历属性A的所有取值v,如果在某取值上集合(数据量)为空,则这个点设置为D中最大类类型,否则递归创建基于数据集Dv和没有属性a*的决策树:

ID3存在很多不足,对可取值较多的属性有偏好;长度,密度等无考虑等,改进版为C4.5
3.C4.5算法
基于信息增益率,定义Gain_ratio,在原信息增益基础上除了IV:
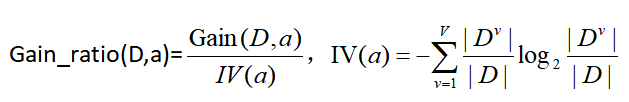
属性a可取值的数目越多,IV(a)越大,因此对数目小的属性有偏好。最终C4.5基于一个启发式:先选出信息增益高于平均的,再从其中选择增益率最高的。
其余和上面的ID3流程一致,只是属性划分有如上细微区别。
ID3/C4.5的防过拟合
预剪枝:生成分支的过程中,先评估当且泛化性能(测试交叉验证等),然后评估划分后的性能,若,划分后不能提升泛化性能,则不划分,还是保留这个叶子节点。
后剪枝:先完全训练完,得到决策树,然后从最底层节点往上,评估把这个节点(父节点,有子节点的)设置为叶子节点和不设置两种情况,若,设置为叶子节点能提升性能,则把这个节点设置为叶子节点,否则保留。
设定最大深度:划分决策树的时候统计深度,超过这个深度了就停止划分,输出为叶子节点。
设定节点最小数据量:节点内划入的数据集小于某个量了,再划分可能没意义了,就不划分了。
随机性:基于信息增益,增益率等评价指标,选择最佳属性的时候,最佳属性可以不一定就是最佳,比如可以是在高于平均的属性里面,随机选择一个作为最佳属性。
ID3/C4.5的缺失数据
定义:

新的计算:
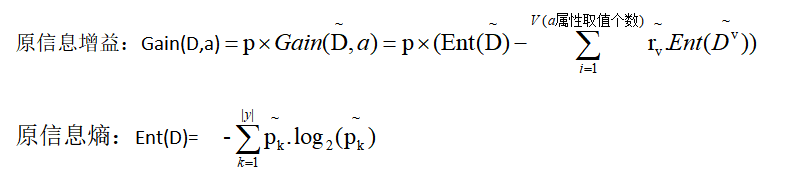
属性划分:在划分x样本时,a属性若取值已知,则x划入取值对应的子结点,权重wx不变;若未知,x划入所有子结点,且按照wx=rv.wx划分权值。
4.CART算法
CART:分类和回归树,是个二叉树。 其希望划分下去的数据方差越来越接近。

1)cart在分类方面:基于基尼系数:Gini(D)

Gini(D)反应的是数据集D中样本不一致的概率,因此Gini越小,越一致性,纯度越高。
属性划分,基尼指数:Gini_index(D,a)

累加D中基于属性a(a1,a2,...,av)划分的不同数据集(a1:D1,a2:D2,...,av:DV)的Gini系数和,反映的是对属性a划分的整体Gini系数评价。
对于连续特征:如属性a身高,取值为:150,160,170,180,可以分别计算基于155,165,175为划分点的二分,分成小于等于划分点,大于划分点的两个数据集D1、D2。如基于165,把所有基于属性a<=165的划入左节点,a>165的划入右节点。然后计算(基尼增益)GiniGain=Gini_index(D1,a)+Gini_index(D2,a),最后选择最小的划分点,如175,把数据划分为两个部分。
对于离散特征:CART分类时,选择最小Gini_index的属性划分,a*=argmin Gini_index(D,a),(遍历所有属性A,遍历属性A中可能的取值a,得到最小Gini_index的a*,以及其所属的属性A*),然后把数据分成属性A*中取值为a*的部分D1,和属性A*中除取值a*外的所有数据部分D2,划入左右节点。
2)cart在回归方面:基于方差/标准差
对于任意划分特征a,对应的任意划分点s两边划分成的数据集D1和D2,求出使D1和D2各自集合的均方差最小,同时D1和D2的均方差之和最小所对应的特征和特征值划分点(c1为D1数据集的样本均值,c2为D2数据集的样本均值):
即:不断基于连续属性数据的中点,做二分划分为左右数据集D1,D2,然后计算均值c1,c2,计算方差,计算方差和,最后取方差最小的划分点作为当且决策树分割点。
而叶子节点的输出:通常采用当前归属到此叶子节点中数据集的均值或者中位数。
阀值:可以定义数据量,比如5,当叶子节点的数据集小于这个量的时候停止划分,之间返回数据集的均值或中位数。
CART的剪枝
白话版:从最小面的子树开始,一直往上到根节点下面的左右子树,依次把每个以 t 为根节点的子树(两个,如果存在的话//有些不一定存在左右子树,比如只存在左子树就只考虑左子树Ttl)Ttl,Ttr,分别计算正常不剪枝时(整个决策树)的训练损失C(Tt),和剪枝记为叶子节点时(叶子节点是值分类为最大类值,回归为平均值)(整个决策树)的训练损失C(T);
然后按照 2)步计算得到这个 t 节点子树节点(Ttl,Ttr)的阀值(阀值为min更新,确保越往上阀值越小);
这样一层层往上计算,得到每个节点的a值了,从2)步更新公式来看,上层的阀值<=下层节点的阀值;
因此4)步选择最大的ak开始,自上而下(从a值上层的阀值<=下层节点的阀值来看,这样首先会剪掉最小面的一些树,然后慢慢往上剪)把小于阀值的减掉得到一决策树T1,以此类推得到集合M个数那么多个剪枝决策树T1,T2,...,T|M|;
然后交叉验证(k折、留一等等),选择误差最小的,作为输出。
总结来说就是一句话:产生很多按照不同强度(阀值a)剪出来的剪枝决策树,然后测试效果,选出一个最好的输出。

sklearn实现:
分类DecisionTreeClassifier
具体参数参考官方文档:https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html
import numpy as np
from sklearn import tree
from graphviz import Source
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
np.random.seed(11)
iris = load_iris()
X = iris.data
Y = iris.target
# 导入数据:用于分类
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, random_state=2, test_size=0.2)
# 决策树分类器,criterion:标准,max_depth:最大深度
clf = tree.DecisionTreeClassifier(criterion='gini', max_depth=3)
clf.fit(X_train, Y_train)
pdy = clf.predict(X_test)
score = clf.score(X_test, Y_test)
print(score)
dot_data = tree.export_graphviz(clf, out_file=None, feature_names=iris.feature_names,
class_names=iris.target_names,
filled=True, rounded=True,
special_characters=True)
graph = Source(dot_data)
graph.format = 'png'
graph.render('cart_tree', view=True)

回归DecisionTreeRegressor
import numpy as np
from sklearn import tree
from graphviz import Source
from sklearn.datasets import load_boston
boston = load_boston()
# 太大不好显示,取前20画CART树
X = boston.data[:20]
y = boston.target[:20]
# 用于测试,随机取5个
index = np.random.randint(20, boston.data.shape[0],5 )
test_X = boston.data[index]
test_y = boston.target[index]
# 导入数据:用于分类
# 决策树回归器,mse:均方误差;max_depth:最大深度5
clf_reg = tree.DecisionTreeRegressor(criterion='mse', random_state=11, max_depth=5)
clf_reg.fit(X, y)
print('测试数据原结果:', test_y)
print('测试数据预测结果:', clf_reg.predict(test_X))
dot_data = tree.export_graphviz(clf_reg, out_file=None, feature_names=boston.feature_names,
filled=True, rounded=True,
special_characters=True)
graph = Source(dot_data)
graph.format = 'png'
graph.render('cart_tree_Regressor', view=True)
# 大致还是很相近的,完全一样不太可能
测试数据原结果: [23. 19.6 30.5 24.4 22.9]
测试数据预测结果: [20.3 17.96666667 22.55 27.1 22.55 ]



 浙公网安备 33010602011771号
浙公网安备 33010602011771号