RL-马尔科夫决策过程(MDP)-原理及实现
目录
参考博客:
1:https://blog.csdn.net/unixtch/article/details/78922936
2:https://www.cnblogs.com/pinard/p/9426283.html
书籍:《深入浅出强化学习原理入门》
1.马尔科夫性
下一个状态state t+1,仅和当且状态state t 有关,数学描述:
2.马尔科夫随机过程
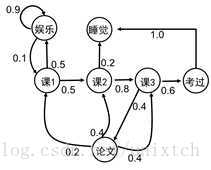
一个随机过程中,任意两个状态之间(下图课1>课2,考过>睡觉)都满足马尔科夫性,那么该随机过程就是一个马尔科夫随机过程,以用一个二元组((S,P)描述,S是该过程的有限状态集合,P是这些状态之间的转移概率矩阵。
S={娱乐,课1,课2,课3,考过,论文,睡觉};
P:p(课1|娱乐)=0.1,p(课2|课1)=0.5,p(课1|娱乐)=0.1,p(课2|课1)=0.5,....,这样的写成矩阵就是P。
3.马尔科夫决策过程(MDP)
其过程由多元组表示(S,A,P,R,γ):
S:(有限)状态集、A:动作集、P:状态转移概率、R:回报函数(或者回报值)、γ:折扣因子,用来计算累积的回报。
这里的转移概率不是前面2在的之间状态1到状态2的概率了,而是状态1通过动作a,变成状态2的概率。如在 t 时刻所处的状态是s,采取a动作后在t+1时刻到达s^的概率为:,也就是状态之间加入了动作和回报
记状态s下采取a动作的概率:;
记累积回报为:
3.1记状态s的状态值函数v(用于评价s的价值)为:
(既:在 t 时刻的状态s的价值函数,是的期望)
3.2状态—行为价值函数q:
(既:状态动作价值有两部分共同决定,1是即时奖励,2是环境可能出现的下一个状态的概率乘以该下一状态的状态价值(下一步的状态期望)且一定比例衰减)
3.3计算形式:
左边,s状态值函数v(s),为s下面的两个(黑点表示)动作执行的概率和动作对应的状态动作价值乘积和。
右边,s状态执行a动作的状态动作价值q(s,a),为s执行a动作(右上黑点)的直接回报,和,未来可能导致的a下面的两个新状态s' 的状态价值及对应概率乘积和共同决定。
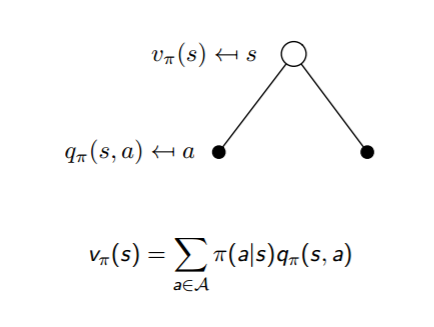
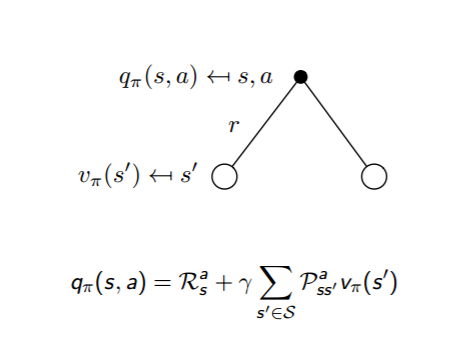
联合起来:
3.4定义最优:
那么马尔科夫决策过程的问题,就是希望找到价值最大的决策过程。
4.实际计算MDP过程
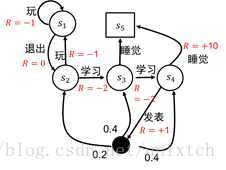
1)给定如下关系,圆形表示状态,s1,s2,s3,s4,终止状态为正方形s5,v(s5)=0
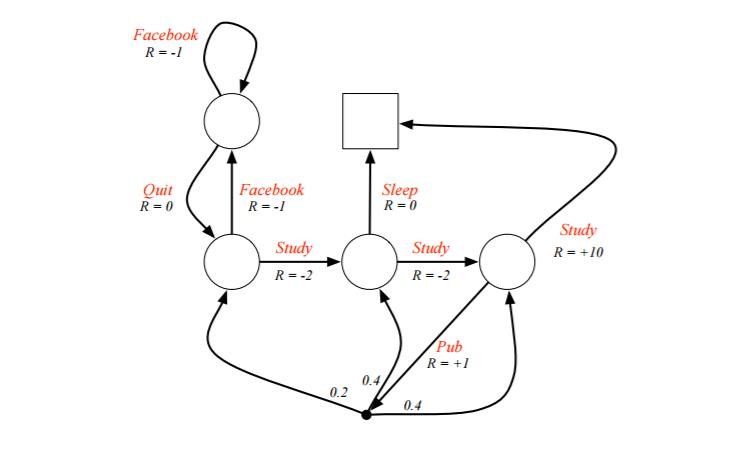
2)假设衰减和状态动作转移概率为:
3)基于3.3计算s1-s4的状态值函数
v(s1)=Facebook动作概率*(Facebook动作直接回报+衰减因子*(下一步状态集合的期望))+Quit动作概率*(0+....)
(这里下一步状态集合的期望直接为下一步状态值,因为这里关系简单,动作的下一步只有一个状态,如果动作的下一步状态可能有多个,还是要按照期望形式求)
解方程:
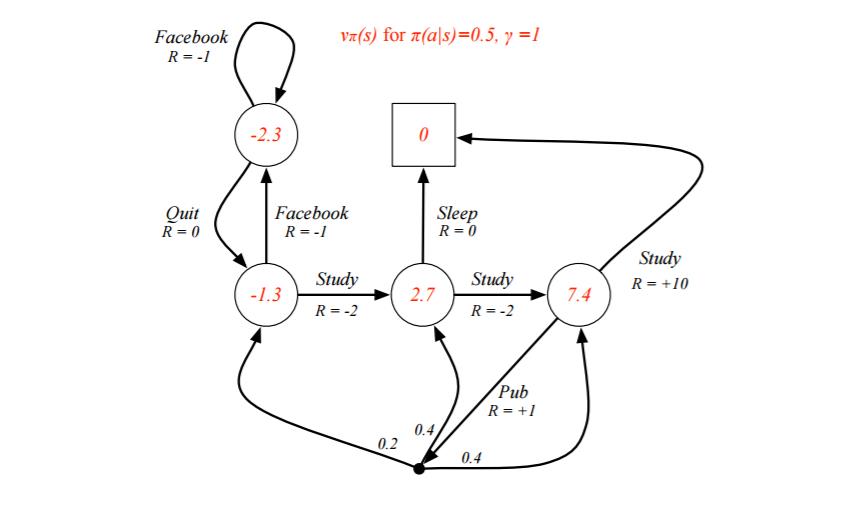
求最大值策略,因为终点:
所以可以回溯,利用:
计算出所有的最优状态动作值函数q*,进而求出最优状态值函数v*

从s1开始,下一个最优状态是s2(q=6>q=6),再下一个是s3(q=6>q=5),是s4(q=8>q=0),然后是终止
s1>s2>s3>s4>end
5.编程初步实现模型
5.1定义游戏规则
1)定义状态为位置状态情况:S={1,2,3,4,5,6,7,8}
self.states = [1,2,3,4,5,6,7,8] #状态空间2)定义动作为东南西北:A={东,南,西,北}
self.actions = ['n','e','s','w']3)定义转移概率这里写死了为,1_s=6:1号南south走为6号,1_e:东走为2号。以此类推
self.t = dict(); #状态转移的数据格式为字典
self.t['1_s'] = 6
self.t['1_e'] = 2
self.t['2_w'] = 1
self.t['2_e'] = 3
self.t['3_s'] = 7
self.t['3_w'] = 2
self.t['3_e'] = 4
self.t['4_w'] = 3
self.t['4_e'] = 5
self.t['5_s'] = 8
self.t['5_w'] = 44)定义回报R:进入1-5回报0,进入6、8回报-1,进入金币7回报1.
self.terminate_states = dict() #终止状态为字典格式
self.terminate_states[6] = 1
self.terminate_states[7] = 1
self.terminate_states[8] = 1
self.rewards = dict(); #回报的数据结构为字典
self.rewards['1_s'] = -1.0
self.rewards['3_s'] = 1.0
self.rewards['5_s'] = -1.05)折扣因子r=0.8
self.gamma = 0.8
则根据当且状态,转到下一步:
def _step(self, action):
#系统当前状态
state = self.state
#判断是否状态在停止字典中(6,7,8停止)
if state in self.terminate_states:
return state, 0, True, {}
#不在则构造字典,进行下一步操作
key = "%d_%s"%(state, action) #将状态和动作组成字典的键值
#状态转移
if key in self.t:
next_state = self.t[key]
else:
next_state = state
self.state = next_state
is_terminal = False
#判断下一步是不是在应该停止状态
if next_state in self.terminate_states:
is_terminal = True
#计算回报值
if key not in self.rewards:
r = 0.0
else:
r = self.rewards[key]
#返回新的状态:下一步,回报值,是否停止,调试信息
return next_state, r,is_terminal,{}这样,只要给上面算法输入一个初始位置state和一个动作action,就会返回下一步的状态next_state和状态回报r。
进而可以按照某概率给出下一步的动作,再次输入到上面的函数,直到遇到退出条件


 浙公网安备 33010602011771号
浙公网安备 33010602011771号