ML聚类：k均值、学习向量量化LVQ、EM/高斯混合GMM、DBSCAN密度聚类、AGNES层次聚类、BIRCH、谱聚类原理推导及实现
目录
3.6 BIRCH层次方法的平衡迭代规约和聚类（Balanced Iterative Reducing and Clustering Using Hierarchies）
一下内容是《机器学习》周志华书籍第九章的个人理解
1.聚类概念
无监标记分类，数据集D={x1,x2,...xm}，xi=(xi1,xi2,...,xin)：如下图：相似据数聚成类
关键：如何描述数据（离散、连续）之间的差异？距离（差异大小）？多大范围内的距离可被认定成一个类？细分多少个类？
2.聚类结果的“好坏”评价指标
通常有2类指标：
1外部指标：参考外部的一些信息、数据；
2内部指标：仅仅利用自身数据得出结论；
2.1外部指标
需要引入外部评价模型，假设这个模型是无条件对的，现在拿这个模型来评价训练出的模型，以评估其好坏。
定义每个簇的伪标签：
从数据集D中任意取一对个（xi,xj）（i<j...(x3,x5)和(x5,x3)等价只取一个）做比较，有如下统计量关系：
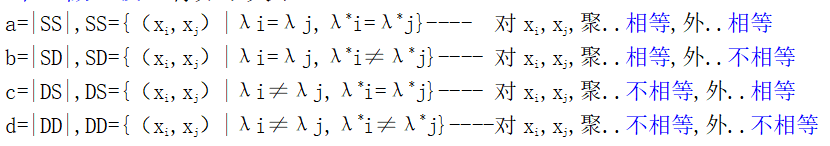
既，对于同一对数据(x3,x5)，外部评价判为(1类，1类)，内部评价均认为是（a类，a类），也就是说内外指标把x3,x5都归结到同一个类别，则记一个SS。这里1和a无关，两个评价体系有自己独立的类标签，只要在他们内部把这一对判为同一类就记为SS。
类似的，外部评价是同一类，内部评价为非同一类，就记一个SD。同样的DS，DD。
最后把这些标记的数量统计起来，a为所有记为SS的对的数量，......b,c,d。
共有m个数据，a+b+c+d=m(m-1)/2对评价。有如下常用的外部衡量指标关系：
Jaccard JC系数：
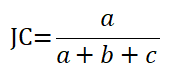
FM指数：
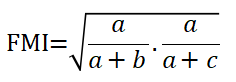
Rand指数：
所有这些计量数∈[0,1]，越大越好。（因为假设外部评价是无条件对的，越大说明内部评价（训练出的模型）越接近外部评价）
2.2内部指标
定义：
有如下衡量指数：
DB指数：
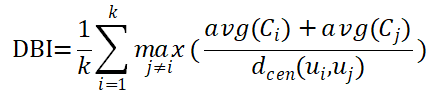
DI指数：
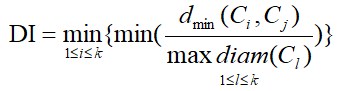
DBI越小越好，DI越大越好。
其它评估标准：
https://blog.csdn.net/sinat_26917383/article/details/70577710
不像监督学习的分类问题和回归问题，无监督聚类没有样本输出，也就没有比较直接的聚类评估方法。但是可以从簇内的稠密程度和簇间的离散程度来评估聚类的效果。常见的有：轮廓系数Silhouette Coefficient和Calinski-Harabasz Index。
1）Calinski-Harabasz分数值s越大则聚类效果越好：
其中m为训练集样本数，k为类别数。Bk为类别之间的协方差矩阵，Wk为类别内部数据的协方差矩阵。tr为矩阵的迹。也就是说，类别内部数据的协方差越小越好，类别之间的协方差越大越好，这样的Calinski-Harabasz分数会高。在scikit-learn中， Calinski-Harabasz Index对应的方法是metrics.calinski_harabaz_score.
2）轮廓系数silhouette（-1,1之间，值越大，聚类效果越好），聚类的质量也相对较好：
对于其中的一个点 i 来说：计算 a(i) = average(i向量到所有它属于的簇中其它点的距离)、计算 b(i) = min (i向量到各个非本身所在簇的所有点的平均距离)，那么 i 向量轮廓系数就为：
2.3距离的计算
上面很多地方用到了距离的计算，样本属性中通常包含离散和连续的，距离计算分为连续有序、离散无序值的计算，这样就是计算样本之间的距离了。
连续、有序的属性：闵可夫斯基距离：
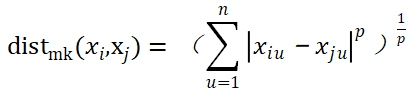，p=2欧氏距离,p=1曼哈顿距离；
离散、无序的属性：VDM（Value Difference Metric）
mu,a：u属性上取值为a的数量；mu,a,i：第i个簇中u属性上取值为a的数量；
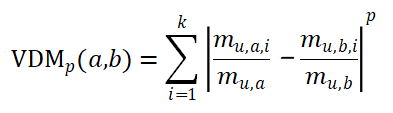
nc个连续与n-nc个离散属性的混合距离：
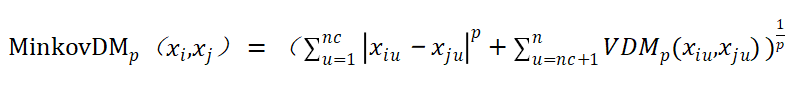
加权距离：
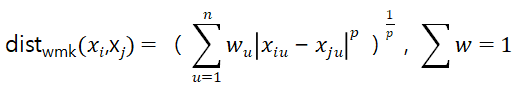
3聚类类算法
这里开始介绍聚类相关算法
3.1 k均值算法
数据集D={x1,x2,...xm}；期望划分后的簇误差最小：
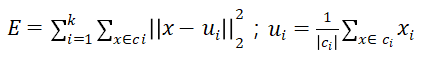
高级扩展：k均值仅在凸形簇结构上表现较好、核k均值、拉普拉斯映射降维后执行k均值
elkan K-Means：利用了两边之和大于等于第三边,以及两边之差小于第三边的三角形性质，来减少KMeans的距离的计算。
K-Means++：把原来初始时随机的选k个点作为初始簇中心做了优化。先随机取一个点作为簇中心，此时只有一个簇，然后计算所有点与簇中心点的距离，距离越大的概率越大，这个概率用来选择第二个簇的中心点，此时有两个簇；然后计算所有点与两个簇中心的距离，取2个距离中小的那个作为样本的计算距离，样本的计算距离越大的概率越大，用于选第3个簇中心，得到3个簇；然后计算所有样本点与3个簇中心的距离，取3个距离中小的那个作为样本的计算距离，......直到得到k个簇中心，作为原始kmeans的随机初始化的替换。
Mini Batch K-Means：在统的K-Means算法中，要计算所有的样本点到所有的质心的距离。如果样本量非常大，比如达到10万以上，特征有100以上，此时用传统的K-Means算法非常的耗时；Mini Batch，用样本集中的一部分的样本来做传统的K-Means，这样可以避免样本量太大时的计算难题，算法收敛速度大大加快。当然此时的代价就是我们的聚类的精确度也会有一些降低。一般来说这个降低的幅度在可以接受的范围之内。
Mini Batch K-Means中，我们会选择一个合适的批样本大小batch size，来做K-Means聚类。一般是通过无放回的随机采样得到的。
3.1.2 实现
scikit-learn中，包括两个K-Means的算法：传统的KMeans、基于采样的MiniBatchKMeans。
KMeans：
KMeans类的主要参数有：
1) n_clusters: 即我们的聚类数量k。
2）max_iter： 最大的迭代次数。
3）n_init：用不同的质心初始化算法的次数。由于K-Means是结果受初始值影响的局部最优的迭代算法，因此需要多跑几次，默认是10。如果k值较大，可适当增大。
4）init： 即初始值选择的方式，完全随机选择'random',优化过的'k-means++'或者自己指定初始化的k个质心。一般建议使用默认的'k-means++'。
5）algorithm：有“auto”, “full” or “elkan”三种选择。"full"是传统的K-Means算法， “elkan”是elkan K-Means算法。默认的"auto"会根据数据值是否是稀疏的，来决定如何选择"full"和“elkan”。一般数据是稠密的，那么就是 “elkan”，否则就是"full"。一般来说建议直接用默认的"auto"import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import KMeans
from sklearn import metrics
# X为样本特征，Y为样本簇类别， 共1000个样本，每个样本5个特征，共4个簇（类），
# 簇中心在[-1,-1], [0,0],[1,1], [2,2]， 簇方差分别为[0.4, 0.2, 0.2,0.2]
X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
cluster_std=[0.4, 0.2, 0.2, 0.2],
random_state=9)
plt.scatter(X[:, 0], X[:, 1], marker='o')
y_pred = KMeans(n_clusters=4, random_state=9).fit_predict(X)
print('Calinski-Harabasz分数:', metrics.calinski_harabaz_score(X, y_pred))
print('silhouette_score轮廓系数:', metrics.silhouette_score(X, y_pred))
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
#
Calinski-Harabasz分数: 5924.050613480169
silhouette_score轮廓系数: 0.6634549555891298
基于采样的MiniBatchKMeans
MiniBatchKMeans类主要参数
MiniBatchKMeans类的主要参数比KMeans类稍多，主要有：
1) n_clusters:一样。
2）max_iter：一样。
3）n_init：用不同的初始化质心运行算法的次数，和KMeans类意义稍有不同的是，MiniBatchKMeans每次用不同的采样数据集来跑不同的初始化质心运行算法。
4）batch_size：算法采样集的大小，默认是100.如果数据集的类别较多或者噪音点较多，需要增加这个值。
5）init： 一样。
6）init_size: 做质心初始值候选的样本个数，默认是batch_size的3倍，一般用默认值就可以了。
7）reassignment_ratio: 某个类别质心被重新赋值的最大次数比例，这个和max_iter一样是为了控制算法运行时间的。这个比例是占样本总数的比例，乘以样本总数就得到了每个类别质心可以重新赋值的次数。如果取值较高的话算法收敛时间可能会增加，尤其是那些暂时拥有样本数较少的质心。默认是0.01。如果数据量不是超大的话，比如1w以下，建议使用默认值。如果数据量超过1w，类别又比较多，可能需要适当减少这个比例值。具体要根据训练集来决定。
8）max_no_improvement：即连续多少个Mini Batch没有改善聚类效果的话，就停止算法， 和reassignment_ratio， max_iter一样是为了控制算法运行时间的。默认是10.一般用默认值就足够了。import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import MiniBatchKMeans
from sklearn import metrics
# X为样本特征，Y为样本簇类别， 共1000个样本，每个样本5个特征，共4个簇（类），
# 簇中心在[-1,-1], [0,0],[1,1], [2,2]， 簇方差分别为[0.4, 0.2, 0.2,0.2]
X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
cluster_std=[0.4, 0.2, 0.2, 0.2],
random_state=9)
plt.scatter(X[:, 0], X[:, 1], marker='o')
y_pred = MiniBatchKMeans(n_clusters=4, batch_size=200, random_state=9).fit_predict(X)
print('Calinski-Harabasz分数:', metrics.calinski_harabaz_score(X, y_pred))
print('silhouette_score轮廓系数:', metrics.silhouette_score(X, y_pred))
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
#
Calinski-Harabasz分数: 2827.388413921534
silhouette_score轮廓系数: 0.5349102143157655
3.2 LVQ学习向量量化算法
前提：假设样本带有标记类型（也可事先通过聚类等算法学到类型）:D={(x1,y1),(x2,y2),...(xm,ym)}
学好之后的模型向量{p1,p2,...,pk}后，可定义一个样本空间X：pi对应其中一个区域Ri，这个区域内的点离pi最近
扩展：提高收敛速度的改进LVQ2、LVQ3
这个算法没有库，需要自己手动实现，感觉理论性不是很强，
3.3 高斯混合GMM
1）与其他聚类算法k-means、LVQ不同的是，以往的聚类分类都是具体的，要么必须是a类，要么必须是b类…;
2）高斯混合聚类GMM给出的是一个概率：样本xj有0.2的概率是男，0.8的概率是女；……..。
3）假设：n维度向量x，假设服从高斯分布，是这个样子：
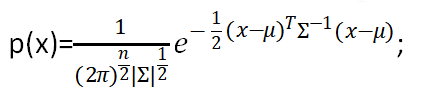
4）问题：GMM的问题是，假如现在我们有一堆数据，知道这一堆是男性，这一堆是女性了，显然我们就可以轻松的计算方差、均值得出高斯分布模型了。但是现在并不知道类别标签。
5）EM算法给出解法。具体GMM的求解在EM之后。也可以直接跳过EM。
3.3.1EM算法
1）EM算法解决这个的思路是先全部假设出来。想象一下平均分米，先随便分，然后多的给少的划入一些，直到大家都感觉差不多了，那其实真就差不了多少了，不信去称一下，重量几乎差不多的。EM就是这么个思路。
2）每个样本都不知道是从哪个分布抽取的，这个时候，对于每一个样本，就有两个东西需要猜测或者估计：
每一个样本属于哪个分布。（是男还是女）、每一个分布对应的参数。（男女分布的均值、方差）
3）基本流程
例：
（a）E初始化参数：先初始化男簇身高的正态分布的参数：如均值=1.7，方差=0.1，女性同样。
（b）E:（有了（a）的参数，就能）计算每一样本更可能属于男生分布或者女生分布了（如男:0.55,女:0.45，于是标记为男）；
（c）M：标为男的有n个样本，现在用这n个样本的数据来重新估计男生身高分布的参数（最大似然估计），女生分布也按照相同的方式估计出来，更新分布。
（d）（c）后，两个分布的参数可能变了，那每个样本的概率又可以从新算了（原来男:0.55,女:0.45更可能属于男的，结果女:0.65,男:0.35更可能是女了），然后重复步骤（1）至（3），直到参数不发生变化收敛为止。
（e）然后我们就神奇的认为，我们学到了这个数据的分布，每个样本的类别标记，并且能拿来预测新的未知样本属于男、女的概率。
4）具体的计算推导
基本流程知道后，核心就是怎么更新参数了，这个在任何一个介绍EM算法里面只会给出一个抽象的概念，因为分布有千万种，更新分布的参数只能抽象来讲。具体来讲会放大下一节高斯混合模型HMM来讲，因为此时分布就是高斯分布，要更新的就是均值和方差。
a）对于m个样本的数据集，如果我们知道m个样本的类型是
，显然，在假设出分布后（如服从高斯分布），概率论中常见的（对数）极大似然法，就能得到我们分布的参数了
然而，如果类型z是未知的，这里面的参数用极大似然是求不出的，因此EM出来解决这个问题，转为可以极大似然求解的迭代形式。
b）额外知识，先看这个Jensen原理：https://blog.csdn.net/jiang425776024/article/details/87992127
Jensen不等式的表述是，如果f(x)是凸函数，x是随机变量，则下面不等式成立：
如果是凹函数：
E是数学期望，对于离散型随机变量，数学期望是求和，对连续型随机变量则为求定积分。如果f(x)是一个严格凹/凸函数，当且仅当x是常数时不等式取等号：
c）假设样本xi为类型zi（隐变量）的概率分布为Qi（什么意思？就是概率的概率分布，xi属于类别zi的概率的概率分布），显然根据分布，必须有这些条件成立：
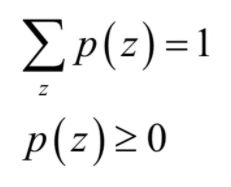
d）利用b）的知识，和c）的概率的概率分布假设，就能对a）中的极大似然目标做转换了，记：
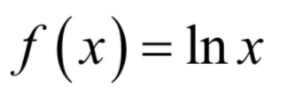
根据b），因为f(x)=lnx为凹函数，所以：
有（注意，f(x)=lnx中的x，被强行看做是p/Qi的期望，Qi为p/Qi的概率；因为累加Qi*(p/Qi)很像是求期望的形式）：
所以最终变为：
显然，这个下界函数更容易求极值，因为对数函数里面已经没有求和项，对参数求导并令导数为0时一般可以得到公式解。去掉上式中为常数的部分，我们要做到，就是不断提高这个下界（极大似然）：
e）EM算法流程
首先初始化参数θ的值（当然不是随机的，要满足概率和为1），接下来循环迭代直至收敛，每次迭代时分为两步：
E步，基于当前的参数（第一次就是基于随机的参数，后面的就是基于计算出来的参数了）估计x的隐变量z的条件概率：（有了θ就能估计属于男、女类的概率）
M步，基于E步参数极大化下界函数：（有了E计算的概率，取概率最大的为样本的类标记，于是就确定了所有类标记，就能用常规的极大似然法了。比如一堆数据男女类别都标好了，假设服从高斯分布，还算不出这个模型的参数了？现在当然能算了，这个M步argmax过程就是这么个极大似然过程。显然很抽象，结合到GMM的时候看到会详细点）
3.3.2 GMM中参数的求解
1）N(均值,方差)为高斯分布，假设有k个类型，wj为第j个分布的权重（j=1,..,k;∑wj=1），则GMM中的概率的概率分布Qi可求（上EM步骤那样，先随机假设出参数。如，分布权重：多少概率属于男，属于女；分布参数：方差、均值）
记Qi = qij，表示样本 xi 属于类 zj 的混合概率（由男女混合分布加成得到，这个概率作为最终类别概率）：
例：
2）极大似然。通过1）我们已经可以知道每个样本的类别标记了（如上例，男:女=0.5625:0.4375，当前样本标记设为男。）
所以可以执行EM的M步极大似然了。展开原式子，替换成高斯分布的形式，方便极大似然的求导：
3）对均值uj,j=1,...,k求导，得到u的更新形式：
以下推导需要两个知识：
矩阵求导：https://blog.csdn.net/jiang425776024/article/details/87388015
多元高斯模型求导：https://blog.csdn.net/SZU_Hadooper/article/details/78090348
4）同理，∑的更新形式可求：
5）最后是wj,j=1,..,k的更新：
根据约束：
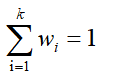
可以构造拉格朗日形式，因为L式子中其它两个不含有w，所以两个∑∑里面直接写成了：
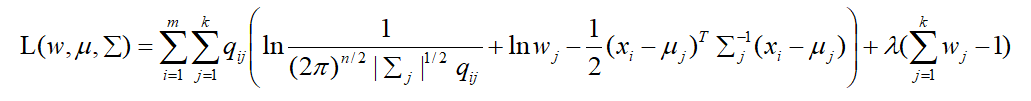
求导：
（纯原创，公式推得很辛苦，麻烦转载刷刷流量，就这点需求了）
6）最终，高斯混合模型的更新方式已全部得出，可以直接按照结论进行更新（第一次随机假设出的那些）参数了。
1.首先初始化μ,∑,w
2.E步，根据模型参数的当前估计值，计算第i个样本来自第j个高斯分布的概率：
3.M步，用极大似然推导公式进行μ,∑,w参数更新：
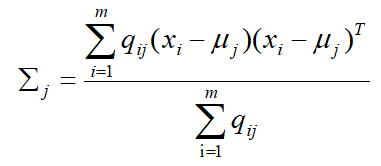
4.参数μ,∑,w几乎不再变化时，样本属于各个类的概率可求，其中最终标记可设为概率最大对应的类。
sklearn Gaussian mixture models API:https://scikit-learn.org/stable/modules/mixture.html
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
from sklearn import mixture
n_samples = 300
n_features = 2
# generate random sample, two components
np.random.seed(0)
# 数据1：generate spherical球形 data centered on (20, 20)
shifted_gaussian = np.random.randn(n_samples, n_features) + np.array([20, 20])
# 数据2：生成零中心拉伸高斯数据,C为矩阵变换用于拉伸数据,中心(0,0)
C = np.array([[0., -0.7], [3.5, .7]])
stretched_gaussian = np.dot(np.random.randn(n_samples, n_features), C)
# 合并数据，竖直
X_train = np.vstack([shifted_gaussian, stretched_gaussian])
'''
fit a Gaussian Mixture Model with two components
covariance_type={‘full’ (default), ‘tied’, ‘diag’, ‘spherical’}控制这每个簇的形状自由度。
默认设置是convariance_type=’diag’,意思是簇在每个维度的尺寸都可以单独设置，但椭圆边界的主轴要与坐标轴平行。
covariance_type=’spherical’时模型通过约束簇的形状，让所有维度相等。这样得到的聚类结果和k-means聚类的特征是相似的，虽然两者并不完全相同。
covariance_type=’full’时，该模型允许每个簇在任意方向上用椭圆建模。
'''
clf = mixture.GaussianMixture(n_components=2, covariance_type='full')
clf.fit(X_train)
plt.scatter(X_train[:, 0], X_train[:, 1], 0.5)
x = np.linspace(-20., 30.)
y = np.linspace(-20., 30.)
X, Y = np.meshgrid(x, y)
XX = np.array([X.ravel(), Y.ravel()]).T
# 预测簇类别
pz = clf.predict(XX).reshape(X.shape)
# 簇概率
prbz = clf.predict_proba(XX).round(5)
print('簇的中点', clf.means_)
print('簇的协方差', clf.covariances_)
# 计算每个样本的加权对数概率。
Z = clf.score_samples(XX)
Z = -Z.reshape(X.shape)
CS = plt.contour(X, Y, Z, norm=LogNorm(vmin=1.0, vmax=1000.0),
levels=np.logspace(0, 3, 10))
CB = plt.colorbar(CS, shrink=0.8, extend='both')
plt.title('Negative log-likelihood predicted by a GMM')
plt.axis('tight')
plt.show()
#
簇的中点 [[19.91453549 19.97556345]
[-0.13607006 -0.07059606]]
3.4 DBSCAN 密度聚类
DBSCAN是一种基于密度的聚类算法，此类算法假设聚类结构能通过样本分布的紧密深度确定，从样本的密度角度来考量样本之间的可连接性，基于可连接样本不断扩张聚类簇以获得最终聚类结果。
1）定义
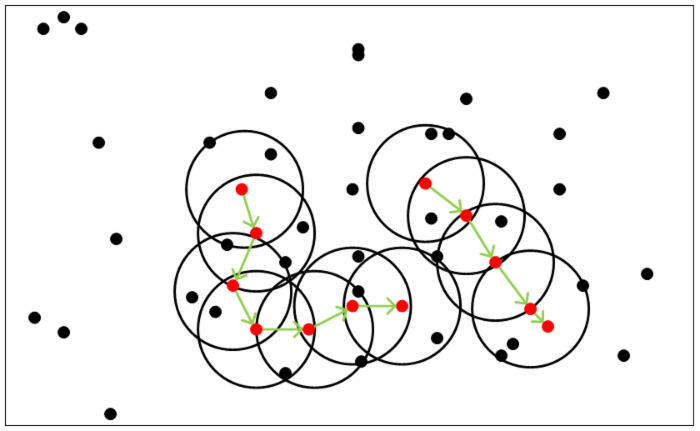
2）DBSCAN算法流程
在scikit-learn中，DBSCAN算法类为sklearn.cluster.DBSCAN
sklearn API:https://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html#sklearn.cluster.DBSCAN
参考中文参数介绍：https://www.cnblogs.com/pinard/p/6217852.html
eps：ϵ-邻域的距离阈值，认值是0.5。
min_samples： 核心对象的ϵ-邻域的样本数阈值。默认值是5。min_samples过大，则核心对象会过少，此时簇内部分本来是一类的样本可能会被标为噪音点，类别数也会变多。反之min_samples过小的话，则会产生大量的核心对象，可能会导致类别数过少。
metric：距离度量参数：欧式距离 “euclidean”、曼哈顿距离 “manhattan”、切比雪夫距离“chebyshev”、闵可夫斯基距离 “minkowski”、带权重闵可夫斯基距离 “wminkowski”、标准化欧式距离 “seuclidean”: 即对于各特征维度做了归一化以后的欧式距离。此时各样本特征维度的均值为0，方差为1、马氏距离“mahalanobis”。
algorithm：最近邻搜索算法参数，‘brute’对应第一种蛮力实现，‘kd_tree’对应第二种KD树实现，‘ball_tree’对应第三种的球树实现， ‘auto’则会在上面三种算法中做权衡，选择一个拟合最好的最优算法
leaf_size：最近邻搜索算法参数，为使用KD树或者球树时， 停止建子树的叶子节点数量的阈值。这个值越小，则生成的KD树或者球树就越大，层数越深，建树时间越长，反之，则生成的KD树或者球树会小，层数较浅，建树时间较短。默认是30. 因为这个值一般只影响算法的运行速度和使用内存大小，因此一般情况下可以不管它。
p: 最近邻距离度量参数。只用于闵可夫斯基距离和带权重闵可夫斯基距离中p值的选择，p=1为曼哈顿距离， p=2为欧式距离。如果使用默认的欧式距离不需要管这个参数。
import numpy as np
from sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs
from sklearn.preprocessing import StandardScaler
# #############################################################################
# Generate sample data
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4,
random_state=0)
# 标准化
X = StandardScaler().fit_transform(X)
# #############################################################################
# 0.3邻域、10核心对象阈值
db = DBSCAN(eps=0.3, min_samples=10).fit(X)
# 全false
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
# 核心样本位置为True
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_
# 计算簇标签, 忽略噪点（label=-1)
n_clusters_ = np.unique(labels).shape[0] - (1 if -1 in labels else 0)
# 计算噪点数量
n_noise_ = labels[labels == -1].shape[0]
print('簇数量: %d' % n_clusters_)
print('噪点数量: %d' % n_noise_)
# #########################衡量指标####################################################
# reference：https://blog.csdn.net/sinat_26917383/article/details/70577710
# homogeneity_score(labels_true, labels_pred)集群标签的同质性度量，得分在0.0到1.0之间。1.0代表完全均匀的标签。
print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
# 集群标签的完整性度量。如果所有数据点都是同一簇的元素，则聚类结果满足完整性。得分在0.0到1.0之间。1.0代表完美的标签
print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
# 同质性和完整性的调和平均
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
# 兰德系数，[-1,1]越大意味着与真实情况越吻合
print("Adjusted Rand Index: %0.3f"
% metrics.adjusted_rand_score(labels_true, labels))
# 互信息，也是衡量吻合度，[-1,1]
print("Adjusted Mutual Information: %0.3f"
% metrics.adjusted_mutual_info_score(labels_true, labels))
# 轮廓系数，适用于实际类型未知情况，[-1,1]同类别样本越近，不同类样本距离越远分数越高
print("Silhouette Coefficient: %0.3f"
% metrics.silhouette_score(X, labels))
# ################################绘图#############################################
# Plot result
import matplotlib.pyplot as plt
# Black removed and is used for noise instead.
unique_labels = set(labels)
colors = [plt.cm.Spectral(each)
for each in np.linspace(0, 1, len(unique_labels))]
# 遍历类别、颜色列表，给不同的簇类画上不同的颜色
for k, col in zip(unique_labels, colors):
# 噪点用黑色
if k == -1:
col = [0, 0, 0, 1]
# 类别为k的bool矩阵
class_member_mask = (labels == k)
# 取类别为k，且core_samples_mask中为True(核心样本位置为True)的位置的样本
# 既，核心样本markersize=14，比非核心样本大
xy = X[class_member_mask & core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
markeredgecolor='k', markersize=14)
# ~ 取反：把1变为0,把0变为1
# 取类别为k，且core_samples_mask中为False(非核心样本位置为False)的位置的样本
# 既，非核心样本markersize=6，比核心样本小
xy = X[class_member_mask & ~core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
markeredgecolor='k', markersize=6)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
output:
簇数量: 3
噪点数量: 18
Homogeneity: 0.953
Completeness: 0.883
V-measure: 0.917
Adjusted Rand Index: 0.952
Adjusted Mutual Information: 0.883
Silhouette Coefficient: 0.626
3.5 AGNES层次聚类
试图从不同层次对数据集进行划分，从而形成树形的聚类结构。自底向上的聚会策略，先将每个样本看做一个聚类簇（m个样本就是m个簇），然后每次运行找出距离最近的两个簇进行合并，不断重复，直到达到设定的k值。注意的是，簇的距离计算的定义：
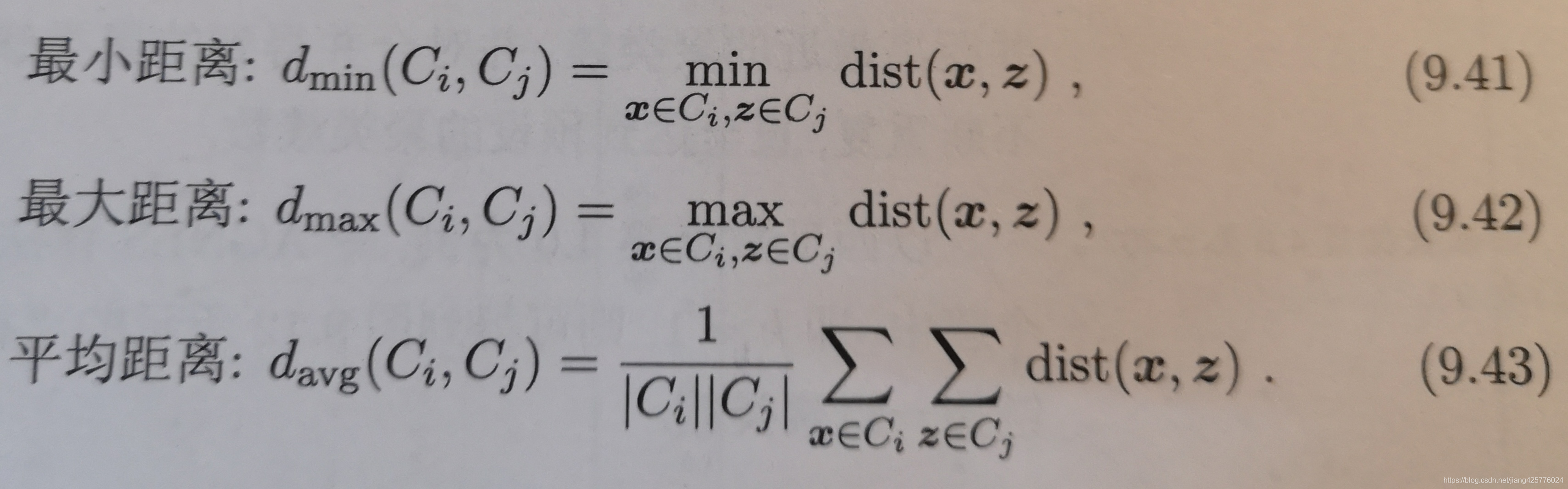
按照这3种min、max、avg计算距离，AGNES算法被称为“单链接”、“全链接”、“均链接”
算法流程（《机器学习》周志华，p215）：
6,7行计算每个样本间相互距离；13-15合并 i* 和 j* 两号的簇并入 i* 内，j* 以后的簇全部更新编号;
17行，删除所有与 j* 号簇有关的距离信息;
19-20行，（只需要）更新第 i* 号簇与其他簇的距离;
图例：
sklearn中没有实现DBSCAN层次聚类的算法，不过这个算法实际操作简单，而且下面有一个更实用的层次聚类算法在sklearn中有实现，因此这个可以看看作为思想，通常更实用的还是下面的Brich算法。
3.6 BIRCH层次方法的平衡迭代规约和聚类（Balanced Iterative Reducing and Clustering Using Hierarchies）
sklearn API:https://scikit-learn.org/stable/modules/generated/sklearn.cluster.Birch.html#sklearn.cluster.Birch
原理介绍：https://www.cnblogs.com/pinard/p/6179132.html
使用介绍:https://www.cnblogs.com/pinard/p/6200579.html
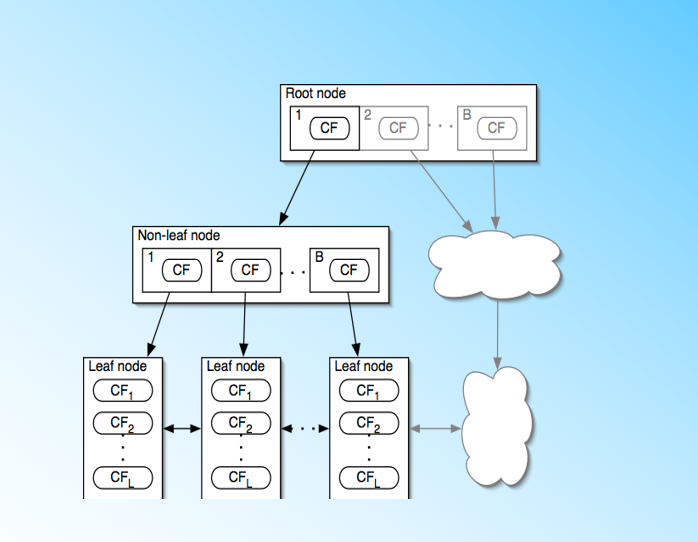
BIRCH算法利用了一个树结构来帮助我们快速的聚类，这个数结构类似于平衡B+树。
优点：速度快、比较适合于数据量大，类别数K也比较多的情况。
3.7 谱聚类（spectral clustering）
原理介绍：https://www.cnblogs.com/pinard/p/6221564.html
使用：https://www.cnblogs.com/pinard/p/6235920.html
谱聚类是从图论中演化出来的算法，后来在聚类中得到了广泛的应用。它的主要思想是把所有的数据看做空间中的点，这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，通过对所有数据点组成的图进行切图，让切图后不同的子图间边权重和尽可能的低，而子图内的边权重和尽可能的高，从而达到聚类的目的。
优缺点：谱聚类只需要数据之间的相似度矩阵，因此对于处理稀疏数据的聚类很有效。由于使用了降维，因此在处理高维数据聚类时的复杂度比传统聚类算法好。聚类的维度非常高，则可能由于降维的幅度不够，谱聚类的运行速度和最后的聚类效果均不好。
