DL-深度神经网络原理推导及PyTorch实现
1.前向传播
引用一个网站的图:




具体来说,就是2行代码,图片中的f为激活函数,这里用sigmoid作为激活函数,事实上有很多其它的套路,这里只讲神经网络的数学原理及初级使用,不会做任何深入扩展:
def feedforward(self, a):
# a:input
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a) + b)
return a
2.反向传播
反向传播主要是前向传播一直传下去,到最最后面的输出层神经元了,然后利用已知数据的标签,和输出成的预测值产生、计算误差,建立成损失函数模型,然后希望损失函数减低,既,求导,利用梯度下降等更新权重参数,以然损失函数往减少的方向去。






可见,有反向传播是从后往前一层层传播的,具体怎么计算更新呢?
1)误差传播的概念
假设现在有100层这样的神经网络,最后第100层显然,就是输出层,我们的目标是学习0-9的数字图片,那么输出层有10个神经元,值为0-1,和为1,表示对应位置的数字的预测概率,如0号神经元0.1,5号神经元0.6,..,最大的概率是5号,如果此时是已经学好了的模型,那么我们就预测说这个数字图片是5了,而问题是一开始并没有学好怎么识别数字,因此关键是学习的过程。
显然,一开始模型是乱输出的,比如图片的真实数字是6,结果输出的预测概率里面最大的是8,如10个输出神经元的输出是:[0.1,0.1,0,0.1,0,0,0,0,0.5,0.2],而训练集给定的真实结果是:[0,0,0,0,0,0,1,0,0,0](为什么这样,因为是标记的百分之百确定的,所有我们知道100%是数字6,其它数字的概率是0%)
显然,[0.1,0.1,0,0.1,0,0,0,0,0.5,0.2]和[0,0,0,0,0,0,1,0,0,0]这两个10维的向量,是可以计算距离的,通常的,直接平方距离被定义成了损失函数记做L,因为理想的时候我们的预测值也应该是输出[0,0,0,0,0,0,1,0,0,0]这种结果,那么这个预测的损失为0,看起来是合理的。
3.理论
1)输出层
最后的输出层比如上面的第100层,记为L层,中间的1-99层记做 根据前向传播输出为
:
2)损失计算函数
3)记公共因子
第100层L层:
第 0-99层 层:
公共因子有如下关系
(这一步很重要),我们发现有了第100层的公共因子,就能得到第99个公共因子
,一以此类推。
4)输出层的梯度
第100层L:
第1-99层 层:
得出这个关系后,每个层的权重更新就可以按照梯度下降等更新了
5)梯度下降更新流程
根据每次更新计算梯度有批量(Batch),小批量(mini-Batch),随机三个变种的梯度下降,小批量用的比较多,每次一定数量均匀起来再更新。
输入: 总层数L,以及各隐藏层与输出层的神经元个数,激活函数,损失函数,迭代步长α,最大迭代次数MAX与停止迭代阈值ϵ,输入的m个训练样本
输出:各隐藏层与输出层的线性关系系数矩阵W和偏倚向量b
按照如下参数更新:(单个样本的)
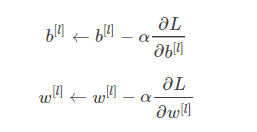
对应的有批量的(取全部样本),小批量的(取随机的小部分样本集),差别只是把求导项由当个变量的更新变成取批量样本的均值做更新。
3.1 激活函数
激活函数保证神经网络模型是非线性的,否则多个神经网络层,最终也是可以表示成线性形式的。
激活函数应该是非线性、几乎处处可导、单调,并尽量避免饱和(为什么?3.5有说明),常见:sigmoid、tanh、ReLU:

3.2 损失函数
前面的平方损失通常用于回归问题,常见的还有机器学习中的交叉熵,主要用于分类。
交叉熵:
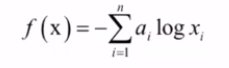
交叉熵有极小值:
意义:当真实概率与预测概率相当,xi=ai时有极小值

3.3 正则化
抵抗过拟合的技巧。
3.4 学习率
应该是接近0的正数。
其它变种,动量项梯度下降,引入动量V:
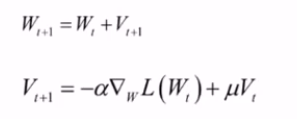

3.5 存在的问题
1)梯度消失问题
如果激活函数导数绝对值<1,多次连乘后,误差项,进而导致对W,b的梯度值接近0!不幸的是,上面用的sigmoid就是这样的一个激活函数,不超过3/5层神经网络,上面那样的全连接网络后面梯度会接近0的。
ReLU一定程度上减少梯度消失问题,但不是绝对的。
2)饱和性
x趋于±无穷时,导数=0,x=c的时候存在导数=0。(上面说了要避免饱和性,梯度消失主要就是激活函数导数接近0,而饱和性的函数可能直接就是0,因此要避免这样的饱和性函数)
3)退化问题
神经网络的训练误差和测试误差会随着层数增加而增大,也就是说并不是层次越多越好,多了可能过拟合。解决技巧有残差网络等。
4)局部极小值
神经网络的优化目标不是一个凸优化问题,很可能存在无法预测的局部极小值,陷入其中很可能就无法跳出,造成效果不好。目前无好的解决办法。
5) 鞍点问题
Hessian矩阵不正定,不是局部极小值点,也就是说可能连局部极小值都找不到!。
以上问题都没有很好的解决办法,可见效果好坏通常还与初始迭代位置点优化,所有目前能做的就是多次尝试(暴力)。
4.基于numpy实现
另一个文章:https://blog.csdn.net/jiang425776024/article/details/85040726
5基于sklearn实现
API:https://scikit-learn.org/stable/modules/classes.html#module-sklearn.neural_network
sklearn 中有3个神经网络的实现库(了解就好,现在神经网络都是PyTorch、TensorFlow、caffe更实际)
neural_network.BernoulliRBM([n_components, …]) |
伯努利限制玻尔兹曼机(RBM) |
neural_network.MLPClassifier([…]) |
多层感知机分类器 |
neural_network.MLPRegressor([…]) |
多层感知机回归器 |
6.基于PyTorch实现
import torch as t
import matplotlib.pyplot as plt
import torch.nn.functional as F
x = t.unsqueeze(t.linspace(-1, 1, 100), dim=1)
y = x.pow(2) + 0.2 * t.rand(x.size())
class Net(t.nn.Module):
def __init__(self, n_feature, n_hidden1, n_hidden2, n_output):
super(Net, self).__init__() # 继承 __init__ 功能
# 定义每层用什么样的形式
self.layer1 = t.nn.Linear(n_feature, n_hidden1) # 隐藏层线性输出
self.layer2 = t.nn.Linear(n_hidden1, n_hidden2) # 隐藏层线性输出
self.predict = t.nn.Linear(n_hidden2, n_output) # 输出层线性输出
def forward(self, x): # 这同时也是 Module 中的 forward 功能
# 正向传播输入值, 神经网络分析出输出值
x = F.relu(self.layer1(x))
x = F.relu(self.layer2(x))
# 最后一层输出不需要激活
x = self.predict(x)
return x
net = Net(n_feature=1, n_hidden1=10, n_hidden2=10, n_output=1)
print(net)
optimizer = t.optim.SGD(net.parameters(), lr=0.2) # 传入 net 的所有参数, 学习率
loss_func = t.nn.MSELoss() # 预测值和真实值的误差计算公式 (均方差)
plt.ion() # 画图
plt.show()
for i in range(100):
inputs = t.autograd.Variable(x)
target = t.autograd.Variable(y)
output = net(inputs) # 喂给 net 训练数据 x, 输出预测值
loss = loss_func(output, target) # 计算两者的误差
optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
optimizer.step() # 将参数更新值施加到 net 的 parameters 上
# 接着上面来
if i % 5 == 0:
plt.cla()
# 原始
plt.scatter(inputs.data.numpy(), target.data.numpy(),label='real')
# 预测
plt.plot(inputs.data.numpy(), output.data.numpy(), 'r-', lw=5,label='predict')
plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
plt.legend()
plt.pause(0.1)
plt.pause(10000000000)

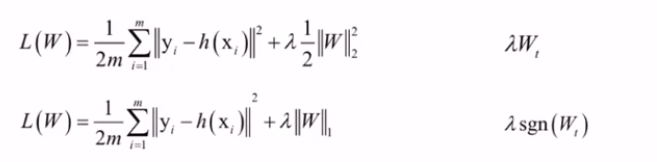

 浙公网安备 33010602011771号
浙公网安备 33010602011771号