LeetCode 1259. Handshakes That Don't Cross

一、原题描述

You are given an even number of people num_people that stand around a circle and each person shakes hands with someone else, so that there are num_people / 2 handshakes total.

Return the number of ways these handshakes could occur such that none of the handshakes cross.

Since this number could be very big, return the answer mod 10^9 + 7

 

Example 1:

Input: num_people = 2
Output: 1

Example 2:

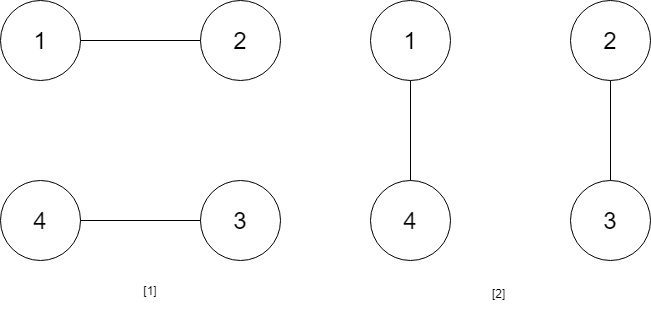
Input: num_people = 4
Output: 2
Explanation: There are two ways to do it, the first way is [(1,2),(3,4)] and the second one is [(2,3),(4,1)].

Example 3:

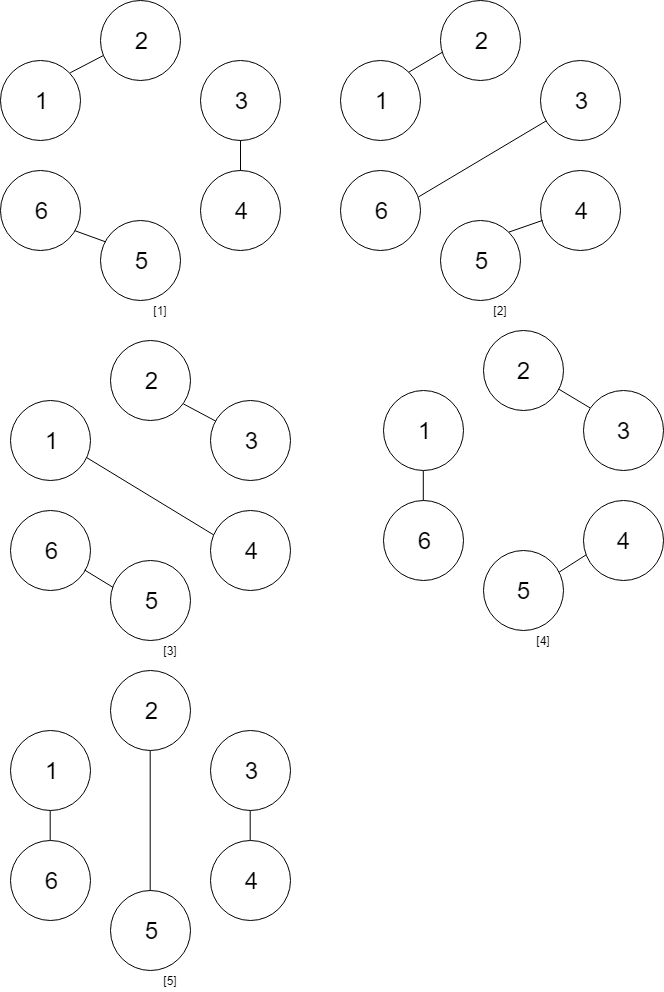
Input: num_people = 6
Output: 5

Example 4:

Input: num_people = 8
Output: 14

 

Constraints:

• 2 <= num_people <= 1000
• num_people % 2 == 0

二、简要翻译

n(偶数)个人围成个圈，两两握手，要求不能交叉握手。求可能的握手方案个数（mod 10^9 + 7）

 

三、思路分析

• 动态规划类问题。可以从上到下或者从下到上来解决这个问题。
• 假设有n个人，数组result[i] 表示i个人构成的子问题的答案。
• 第一个人只能和第2，4，6，8 ... 个人握手。根据握手结果将圆分成两个半球。
• result[n] = result[0] * result[n-2] + result[2] * result[n-4] + result[4] * result[n-6] +...+ result[n-2] * result[0]
• 循环计算的时候注意要mod 10^9 + 7
• 这应该是分类成medium的问题吧。

 

 

四、代码

public int numberOfWays(int num_people) {
        int mod = (int) 1e9 + 7;
        int len = num_people / 2;
        long[] results = new long[len + 1];
        results[0] = 1;
        results[1] = 1;
        long result;
        for (int i = 2; i <= len; i++) {
            result = 0;
            for (int j = 1; j <= i; j++) {
                result += (results[j - 1] * results[i - j]) % mod;
                result %= mod;
            }
            results[i] = result;
        }
        return (int) results[len];
    }