基于celeba数据集和pytorch框架实现dcgan的人脸图像生成
参考pytorch的官方教程实现了dcgan网络,对官方的实例进行了如下修改。
(1)把原来的script修组织成了类的形式,直接复制官方的代码无法直接运行,通过类的形式管理数据和函数更加方便
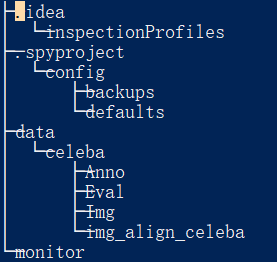
(2)添加了训练过程的图形化保存,官方给的实例中是pyplot的show的形式显示结果,改成了savefig的方式保存图像,训练过程的图像保存在monitor文件夹
(3)调用imagemagick的方式保存gif图,
(4)dcgan训练celeba数据集,该数据集下载后放在和dcgan.py相同的目录下,名词为data,包含celeba,而celeba包含Anno,Eval和img_align_celeba文件件,202599个人脸图像样本
全部代码如下:
# -*- coding: utf-8 -*-
"""
DCGAN Tutorial
==============
**Author**: `Nathan Inkawhich <https://github.com/inkawhich>`__
"""
######################################################################
# Introduction
# ------------
#
# This tutorial will give an introduction to DCGANs through an example. We
# will train a generative adversarial network (GAN) to generate new
# celebrities after showing it pictures of many real celebrities. Most of
# the code here is from the dcgan implementation in
# `pytorch/examples <https://github.com/pytorch/examples>`__, and this
# document will give a thorough explanation of the implementation and shed
# light on how and why this model works. But don’t worry, no prior
# knowledge of GANs is required, but it may require a first-timer to spend
# some time reasoning about what is actually happening under the hood.
# Also, for the sake of time it will help to have a GPU, or two. Lets
# start from the beginning.
#
# Generative Adversarial Networks
# -------------------------------
#
# What is a GAN?
# ~~~~~~~~~~~~~~
#
# GANs are a framework for teaching a DL model to capture the training
# data’s distribution so we can generate new data from that same
# distribution. GANs were invented by Ian Goodfellow in 2014 and first
# described in the paper `Generative Adversarial
# Nets <https://papers.nips.cc/paper/5423-generative-adversarial-nets.pdf>`__.
# They are made of two distinct models, a *generator* and a
# *discriminator*. The job of the generator is to spawn ‘fake’ images that
# look like the training images. The job of the discriminator is to look
# at an image and output whether or not it is a real training image or a
# fake image from the generator. During training, the generator is
# constantly trying to outsmart the discriminator by generating better and
# better fakes, while the discriminator is working to become a better
# detective and correctly classify the real and fake images. The
# equilibrium of this game is when the generator is generating perfect
# fakes that look as if they came directly from the training data, and the
# discriminator is left to always guess at 50% confidence that the
# generator output is real or fake.
#
# Now, lets define some notation to be used throughout tutorial starting
# with the discriminator. Let :math:`x` be data representing an image.
# :math:`D(x)` is the discriminator network which outputs the (scalar)
# probability that :math:`x` came from training data rather than the
# generator. Here, since we are dealing with images the input to
# :math:`D(x)` is an image of CHW size 3x64x64. Intuitively, :math:`D(x)`
# should be HIGH when :math:`x` comes from training data and LOW when
# :math:`x` comes from the generator. :math:`D(x)` can also be thought of
# as a traditional binary classifier.
#
# For the generator’s notation, let :math:`z` be a latent space vector
# sampled from a standard normal distribution. :math:`G(z)` represents the
# generator function which maps the latent vector :math:`z` to data-space.
# The goal of :math:`G` is to estimate the distribution that the training
# data comes from (:math:`p_{data}`) so it can generate fake samples from
# that estimated distribution (:math:`p_g`).
#
# So, :math:`D(G(z))` is the probability (scalar) that the output of the
# generator :math:`G` is a real image. As described in `Goodfellow’s
# paper <https://papers.nips.cc/paper/5423-generative-adversarial-nets.pdf>`__,
# :math:`D` and :math:`G` play a minimax game in which :math:`D` tries to
# maximize the probability it correctly classifies reals and fakes
# (:math:`logD(x)`), and :math:`G` tries to minimize the probability that
# :math:`D` will predict its outputs are fake (:math:`log(1-D(G(x)))`).
# From the paper, the GAN loss function is
#
# .. math:: \underset{G}{\text{min}} \underset{D}{\text{max}}V(D,G) = \mathbb{E}_{x\sim p_{data}(x)}\big[logD(x)\big] + \mathbb{E}_{z\sim p_{z}(z)}\big[log(1-D(G(z)))\big]
#
# In theory, the solution to this minimax game is where
# :math:`p_g = p_{data}`, and the discriminator guesses randomly if the
# inputs are real or fake. However, the convergence theory of GANs is
# still being actively researched and in reality models do not always
# train to this point.
#
# What is a DCGAN?
# ~~~~~~~~~~~~~~~~
#
# A DCGAN is a direct extension of the GAN described above, except that it
# explicitly uses convolutional and convolutional-transpose layers in the
# discriminator and generator, respectively. It was first described by
# Radford et. al. in the paper `Unsupervised Representation Learning With
# Deep Convolutional Generative Adversarial
# Networks <https://arxiv.org/pdf/1511.06434.pdf>`__. The discriminator
# is made up of strided
# `convolution <https://pytorch.org/docs/stable/nn.html#torch.nn.Conv2d>`__
# layers, `batch
# norm <https://pytorch.org/docs/stable/nn.html#torch.nn.BatchNorm2d>`__
# layers, and
# `LeakyReLU <https://pytorch.org/docs/stable/nn.html#torch.nn.LeakyReLU>`__
# activations. The input is a 3x64x64 input image and the output is a
# scalar probability that the input is from the real data distribution.
# The generator is comprised of
# `convolutional-transpose <https://pytorch.org/docs/stable/nn.html#torch.nn.ConvTranspose2d>`__
# layers, batch norm layers, and
# `ReLU <https://pytorch.org/docs/stable/nn.html#relu>`__ activations. The
# input is a latent vector, :math:`z`, that is drawn from a standard
# normal distribution and the output is a 3x64x64 RGB image. The strided
# conv-transpose layers allow the latent vector to be transformed into a
# volume with the same shape as an image. In the paper, the authors also
# give some tips about how to setup the optimizers, how to calculate the
# loss functions, and how to initialize the model weights, all of which
# will be explained in the coming sections.
#
from __future__ import print_function
#%matplotlib inline
import argparse
import os
import random
import torch
import torch.nn as nn
import torch.nn.parallel
import torch.backends.cudnn as cudnn
import torch.optim as optim
import torch.utils.data
import torchvision.datasets as dset
import torchvision.transforms as transforms
import torchvision.utils as vutils
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML
def setRandom():
# Set random seed for reproducibility
manualSeed = 999
#manualSeed = random.randint(1, 10000) # use if you want new results
print("Random Seed: ", manualSeed)
random.seed(manualSeed)
torch.manual_seed(manualSeed)
######################################################################
# Inputs
# ------
#
# Let’s define some inputs for the run:
#
# - **dataroot** - the path to the root of the dataset folder. We will
# talk more about the dataset in the next section
# - **workers** - the number of worker threads for loading the data with
# the DataLoader
# - **batch_size** - the batch size used in training. The DCGAN paper
# uses a batch size of 128
# - **image_size** - the spatial size of the images used for training.
# This implementation defaults to 64x64. If another size is desired,
# the structures of D and G must be changed. See
# `here <https://github.com/pytorch/examples/issues/70>`__ for more
# details
# - **nc** - number of color channels in the input images. For color
# images this is 3
# - **nz** - length of latent vector
# - **ngf** - relates to the depth of feature maps carried through the
# generator
# - **ndf** - sets the depth of feature maps propagated through the
# discriminator
# - **num_epochs** - number of training epochs to run. Training for
# longer will probably lead to better results but will also take much
# longer
# - **lr** - learning rate for training. As described in the DCGAN paper,
# this number should be 0.0002
# - **beta1** - beta1 hyperparameter for Adam optimizers. As described in
# paper, this number should be 0.5
# - **ngpu** - number of GPUs available. If this is 0, code will run in
# CPU mode. If this number is greater than 0 it will run on that number
# of GPUs
#
# Root directory for dataset
dataroot = "data/celeba"
# Number of workers for dataloader
workers = 2
# Batch size during training
batch_size = 128
# Spatial size of training images. All images will be resized to this
# size using a transformer.
image_size = 64
# Number of channels in the training images. For color images this is 3
nc = 3
# Size of z latent vector (i.e. size of generator input)
nz = 100
# Size of feature maps in generator
ngf = 64
# Size of feature maps in discriminator
ndf = 64
# Number of training epochs
num_epochs = 5
# Learning rate for optimizers
lr = 0.0002
# Beta1 hyperparam for Adam optimizers
beta1 = 0.5
# Number of GPUs available. Use 0 for CPU mode.
ngpu = 1
######################################################################
# Generator
# ~~~~~~~~~
#
# The generator, :math:`G`, is designed to map the latent space vector
# (:math:`z`) to data-space. Since our data are images, converting
# :math:`z` to data-space means ultimately creating a RGB image with the
# same size as the training images (i.e. 3x64x64). In practice, this is
# accomplished through a series of strided two dimensional convolutional
# transpose layers, each paired with a 2d batch norm layer and a relu
# activation. The output of the generator is fed through a tanh function
# to return it to the input data range of :math:`[-1,1]`. It is worth
# noting the existence of the batch norm functions after the
# conv-transpose layers, as this is a critical contribution of the DCGAN
# paper. These layers help with the flow of gradients during training. An
# image of the generator from the DCGAN paper is shown below.
#
# .. figure:: /_static/img/dcgan_generator.png
# :alt: dcgan_generator
#
# Notice, the how the inputs we set in the input section (*nz*, *ngf*, and
# *nc*) influence the generator architecture in code. *nz* is the length
# of the z input vector, *ngf* relates to the size of the feature maps
# that are propagated through the generator, and *nc* is the number of
# channels in the output image (set to 3 for RGB images). Below is the
# code for the generator.
#
# Generator Code
class Generator(nn.Module):
def __init__(self, ngpu):
super(Generator, self).__init__()
self.ngpu = ngpu
self.main = nn.Sequential(
# input is Z, going into a convolution
nn.ConvTranspose2d( nz, ngf * 8, 4, 1, 0, bias=False),
nn.BatchNorm2d(ngf * 8),
nn.ReLU(True),
# state size. (ngf*8) x 4 x 4
nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
nn.BatchNorm2d(ngf * 4),
nn.ReLU(True),
# state size. (ngf*4) x 8 x 8
nn.ConvTranspose2d( ngf * 4, ngf * 2, 4, 2, 1, bias=False),
nn.BatchNorm2d(ngf * 2),
nn.ReLU(True),
# state size. (ngf*2) x 16 x 16
nn.ConvTranspose2d( ngf * 2, ngf, 4, 2, 1, bias=False),
nn.BatchNorm2d(ngf),
nn.ReLU(True),
# state size. (ngf) x 32 x 32
nn.ConvTranspose2d( ngf, nc, 4, 2, 1, bias=False),
nn.Tanh()
# state size. (nc) x 64 x 64
)
def forward(self, input):
return self.main(input)
######################################################################
# Discriminator
# ~~~~~~~~~~~~~
#
# As mentioned, the discriminator, :math:`D`, is a binary classification
# network that takes an image as input and outputs a scalar probability
# that the input image is real (as opposed to fake). Here, :math:`D` takes
# a 3x64x64 input image, processes it through a series of Conv2d,
# BatchNorm2d, and LeakyReLU layers, and outputs the final probability
# through a Sigmoid activation function. This architecture can be extended
# with more layers if necessary for the problem, but there is significance
# to the use of the strided convolution, BatchNorm, and LeakyReLUs. The
# DCGAN paper mentions it is a good practice to use strided convolution
# rather than pooling to downsample because it lets the network learn its
# own pooling function. Also batch norm and leaky relu functions promote
# healthy gradient flow which is critical for the learning process of both
# :math:`G` and :math:`D`.
#
#########################################################################
# Discriminator Code
class Discriminator(nn.Module):
def __init__(self, ngpu):
super(Discriminator, self).__init__()
self.ngpu = ngpu
self.main = nn.Sequential(
# input is (nc) x 64 x 64
nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
nn.LeakyReLU(0.2, inplace=True),
# state size. (ndf) x 32 x 32
nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
nn.BatchNorm2d(ndf * 2),
nn.LeakyReLU(0.2, inplace=True),
# state size. (ndf*2) x 16 x 16
nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
nn.BatchNorm2d(ndf * 4),
nn.LeakyReLU(0.2, inplace=True),
# state size. (ndf*4) x 8 x 8
nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
nn.BatchNorm2d(ndf * 8),
nn.LeakyReLU(0.2, inplace=True),
# state size. (ndf*8) x 4 x 4
nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
nn.Sigmoid()
)
def forward(self, input):
return self.main(input)
class DCGAN:
######################################################################
# Data
# ----
#
# In this tutorial we will use the `Celeb-A Faces
# dataset <http://mmlab.ie.cuhk.edu.hk/projects/CelebA.html>`__ which can
# be downloaded at the linked site, or in `Google
# Drive <https://drive.google.com/drive/folders/0B7EVK8r0v71pTUZsaXdaSnZBZzg>`__.
# The dataset will download as a file named *img_align_celeba.zip*. Once
# downloaded, create a directory named *celeba* and extract the zip file
# into that directory. Then, set the *dataroot* input for this notebook to
# the *celeba* directory you just created. The resulting directory
# structure should be:
#
# ::
#
# /path/to/celeba
# -> img_align_celeba
# -> 188242.jpg
# -> 173822.jpg
# -> 284702.jpg
# -> 537394.jpg
# ...
#
# This is an important step because we will be using the ImageFolder
# dataset class, which requires there to be subdirectories in the
# dataset’s root folder. Now, we can create the dataset, create the
# dataloader, set the device to run on, and finally visualize some of the
# training data.
#
def prepareData(self):
# We can use an image folder dataset the way we have it setup.
# Create the dataset
self.dataset = dset.ImageFolder(root=dataroot,
transform=transforms.Compose([
transforms.Resize(image_size),
transforms.CenterCrop(image_size),
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
]))
# Create the dataloader
self.dataloader = torch.utils.data.DataLoader(self.dataset, batch_size=batch_size,
shuffle=True, num_workers=workers)
# Decide which device we want to run on
self.device = torch.device("cuda:0" if (torch.cuda.is_available() and ngpu > 0) else "cpu")
# Plot some training images
real_batch = next(iter(self.dataloader))
plt.figure(figsize=(8,8))
plt.axis("off")
plt.title("Training Images")
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(self.device)[:64], padding=2, normalize=True).cpu(),(1,2,0)))
######################################################################
# Implementation
# --------------
#
# With our input parameters set and the dataset prepared, we can now get
# into the implementation. We will start with the weigth initialization
# strategy, then talk about the generator, discriminator, loss functions,
# and training loop in detail.
#
# Weight Initialization
# ~~~~~~~~~~~~~~~~~~~~~
#
# From the DCGAN paper, the authors specify that all model weights shall
# be randomly initialized from a Normal distribution with mean=0,
# stdev=0.02. The ``weights_init`` function takes an initialized model as
# input and reinitializes all convolutional, convolutional-transpose, and
# batch normalization layers to meet this criteria. This function is
# applied to the models immediately after initialization.
#
# custom weights initialization called on netG and netD
def weights_init(self, m):
classname = m.__class__.__name__
if classname.find('Conv') != -1:
nn.init.normal_(m.weight.data, 0.0, 0.02)
elif classname.find('BatchNorm') != -1:
nn.init.normal_(m.weight.data, 1.0, 0.02)
nn.init.constant_(m.bias.data, 0)
def createGen(self):
######################################################################
# Now, we can instantiate the generator and apply the ``weights_init``
# function. Check out the printed model to see how the generator object is
# structured.
#
# Create the generator
self.netG = Generator(ngpu).to(self.device)
# Handle multi-gpu if desired
if (self.device.type == 'cuda') and (ngpu > 1):
self.netG = nn.DataParallel(self.netG, list(range(ngpu)))
# Apply the weights_init function to randomly initialize all weights
# to mean=0, stdev=0.2.
self.netG.apply(self.weights_init)
# Print the model
print(self.netG)
def createDis(self):
######################################################################
# Now, as with the generator, we can create the discriminator, apply the
# ``weights_init`` function, and print the model’s structure.
#
# Create the Discriminator
self.netD = Discriminator(ngpu).to(self.device)
# Handle multi-gpu if desired
if (self.device.type == 'cuda') and (ngpu > 1):
self.netD = nn.DataParallel(self.netD, list(range(ngpu)))
# Apply the weights_init function to randomly initialize all weights
# to mean=0, stdev=0.2.
self.netD.apply(self.weights_init)
# Print the model
print(self.netD)
def setLossAndOptimizer(self):
######################################################################
# Loss Functions and Optimizers
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#
# With :math:`D` and :math:`G` setup, we can specify how they learn
# through the loss functions and optimizers. We will use the Binary Cross
# Entropy loss
# (`BCELoss <https://pytorch.org/docs/stable/nn.html#torch.nn.BCELoss>`__)
# function which is defined in PyTorch as:
#
# .. math:: \ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - \left[ y_n \cdot \log x_n + (1 - y_n) \cdot \log (1 - x_n) \right]
#
# Notice how this function provides the calculation of both log components
# in the objective function (i.e. :math:`log(D(x))` and
# :math:`log(1-D(G(z)))`). We can specify what part of the BCE equation to
# use with the :math:`y` input. This is accomplished in the training loop
# which is coming up soon, but it is important to understand how we can
# choose which component we wish to calculate just by changing :math:`y`
# (i.e. GT labels).
#
# Next, we define our real label as 1 and the fake label as 0. These
# labels will be used when calculating the losses of :math:`D` and
# :math:`G`, and this is also the convention used in the original GAN
# paper. Finally, we set up two separate optimizers, one for :math:`D` and
# one for :math:`G`. As specified in the DCGAN paper, both are Adam
# optimizers with learning rate 0.0002 and Beta1 = 0.5. For keeping track
# of the generator’s learning progression, we will generate a fixed batch
# of latent vectors that are drawn from a Gaussian distribution
# (i.e. fixed_noise) . In the training loop, we will periodically input
# this fixed_noise into :math:`G`, and over the iterations we will see
# images form out of the noise.
#
# Initialize BCELoss function
self.criterion = nn.BCELoss()
# Create batch of latent vectors that we will use to visualize
# the progression of the generator
self.fixed_noise = torch.randn(64, nz, 1, 1, device=self.device)
# Establish convention for real and fake labels during training
self.real_label = 1.
self.fake_label = 0.
# Setup Adam optimizers for both G and D
self.optimizerD = optim.Adam(self.netD.parameters(), lr=lr, betas=(beta1, 0.999))
self.optimizerG = optim.Adam(self.netG.parameters(), lr=lr, betas=(beta1, 0.999))
def train(self):
######################################################################
# Training
# ~~~~~~~~
#
# Finally, now that we have all of the parts of the GAN framework defined,
# we can train it. Be mindful that training GANs is somewhat of an art
# form, as incorrect hyperparameter settings lead to mode collapse with
# little explanation of what went wrong. Here, we will closely follow
# Algorithm 1 from Goodfellow’s paper, while abiding by some of the best
# practices shown in `ganhacks <https://github.com/soumith/ganhacks>`__.
# Namely, we will “construct different mini-batches for real and fake”
# images, and also adjust G’s objective function to maximize
# :math:`logD(G(z))`. Training is split up into two main parts. Part 1
# updates the Discriminator and Part 2 updates the Generator.
#
# **Part 1 - Train the Discriminator**
#
# Recall, the goal of training the discriminator is to maximize the
# probability of correctly classifying a given input as real or fake. In
# terms of Goodfellow, we wish to “update the discriminator by ascending
# its stochastic gradient”. Practically, we want to maximize
# :math:`log(D(x)) + log(1-D(G(z)))`. Due to the separate mini-batch
# suggestion from ganhacks, we will calculate this in two steps. First, we
# will construct a batch of real samples from the training set, forward
# pass through :math:`D`, calculate the loss (:math:`log(D(x))`), then
# calculate the gradients in a backward pass. Secondly, we will construct
# a batch of fake samples with the current generator, forward pass this
# batch through :math:`D`, calculate the loss (:math:`log(1-D(G(z)))`),
# and *accumulate* the gradients with a backward pass. Now, with the
# gradients accumulated from both the all-real and all-fake batches, we
# call a step of the Discriminator’s optimizer.
#
# **Part 2 - Train the Generator**
#
# As stated in the original paper, we want to train the Generator by
# minimizing :math:`log(1-D(G(z)))` in an effort to generate better fakes.
# As mentioned, this was shown by Goodfellow to not provide sufficient
# gradients, especially early in the learning process. As a fix, we
# instead wish to maximize :math:`log(D(G(z)))`. In the code we accomplish
# this by: classifying the Generator output from Part 1 with the
# Discriminator, computing G’s loss *using real labels as GT*, computing
# G’s gradients in a backward pass, and finally updating G’s parameters
# with an optimizer step. It may seem counter-intuitive to use the real
# labels as GT labels for the loss function, but this allows us to use the
# :math:`log(x)` part of the BCELoss (rather than the :math:`log(1-x)`
# part) which is exactly what we want.
#
# Finally, we will do some statistic reporting and at the end of each
# epoch we will push our fixed_noise batch through the generator to
# visually track the progress of G’s training. The training statistics
# reported are:
#
# - **Loss_D** - discriminator loss calculated as the sum of losses for
# the all real and all fake batches (:math:`log(D(x)) + log(D(G(z)))`).
# - **Loss_G** - generator loss calculated as :math:`log(D(G(z)))`
# - **D(x)** - the average output (across the batch) of the discriminator
# for the all real batch. This should start close to 1 then
# theoretically converge to 0.5 when G gets better. Think about why
# this is.
# - **D(G(z))** - average discriminator outputs for the all fake batch.
# The first number is before D is updated and the second number is
# after D is updated. These numbers should start near 0 and converge to
# 0.5 as G gets better. Think about why this is.
#
# **Note:** This step might take a while, depending on how many epochs you
# run and if you removed some data from the dataset.
#
# Training Loop
# Lists to keep track of progress
self.img_list = []
self.G_losses = []
self.D_losses = []
iters = 0
print("Starting Training Loop...")
# For each epoch
for epoch in range(num_epochs):
# For each batch in the dataloader
for i, data in enumerate(self.dataloader, 0):
############################
# (1) Update D network: maximize log(D(x)) + log(1 - D(G(z)))
###########################
## Train with all-real batch
self.netD.zero_grad()
# Format batch
real_cpu = data[0].to(self.device)
b_size = real_cpu.size(0)
label = torch.full((b_size,), self.real_label, dtype=torch.float, device=self.device)
# Forward pass real batch through D
output = self.netD(real_cpu).view(-1)
# Calculate loss on all-real batch
errD_real = self.criterion(output, label)
# Calculate gradients for D in backward pass
errD_real.backward()
D_x = output.mean().item()
## Train with all-fake batch
# Generate batch of latent vectors
noise = torch.randn(b_size, nz, 1, 1, device=self.device)
# Generate fake image batch with G
fake = self.netG(noise)
label.fill_(self.fake_label)
# Classify all fake batch with D
output = self.netD(fake.detach()).view(-1)
# Calculate D's loss on the all-fake batch
errD_fake = self.criterion(output, label)
# Calculate the gradients for this batch
errD_fake.backward()
D_G_z1 = output.mean().item()
# Add the gradients from the all-real and all-fake batches
errD = errD_real + errD_fake
# Update D
self.optimizerD.step()
############################
# (2) Update G network: maximize log(D(G(z)))
###########################
self.netG.zero_grad()
label.fill_(self.real_label) # fake labels are real for generator cost
# Since we just updated D, perform another forward pass of all-fake batch through D
output = self.netD(fake).view(-1)
# Calculate G's loss based on this output
errG = self.criterion(output, label)
# Calculate gradients for G
errG.backward()
D_G_z2 = output.mean().item()
# Update G
self.optimizerG.step()
# Output training stats
if i % 50 == 0:
print('[%d/%d][%d/%d]\tLoss_D: %.4f\tLoss_G: %.4f\tD(x): %.4f\tD(G(z)): %.4f / %.4f'
% (epoch, num_epochs, i, len(self.dataloader),
errD.item(), errG.item(), D_x, D_G_z1, D_G_z2))
# Save Losses for plotting later
self.G_losses.append(errG.item())
self.D_losses.append(errD.item())
# Check how the generator is doing by saving G's output on fixed_noise
if (iters % 500 == 0) or ((epoch == num_epochs-1) and (i == len(self.dataloader)-1)):
with torch.no_grad():
fake = self.netG(self.fixed_noise).detach().cpu()
self.img_list.append(vutils.make_grid(fake, padding=2, normalize=True))
#save the plot
train_loss_filename='.\monitor\epoch_'+str(epoch)+'_batch_'+str(i)+'_trainloss.jpg'
self.plotSaveTrainLoss(train_loss_filename)
gen_progression_filename='.\monitor\epoch_'+str(epoch)+'_batch_'+str(i)+'_gprogression.gif'
self.plotSaveGprogression(gen_progression_filename)
real_vs_fake_image_filename='.\monitor\epoch_'+str(epoch)+'_batch_'+str(i)+'_read_vs_fake_image.jpg'
self.plotSaveRealFakeImage(real_vs_fake_image_filename)
iters += 1
def plotSaveTrainLoss(self, pic_filename):
######################################################################
# Results
# -------
#
# Finally, lets check out how we did. Here, we will look at three
# different results. First, we will see how D and G’s losses changed
# during training. Second, we will visualize G’s output on the fixed_noise
# batch for every epoch. And third, we will look at a batch of real data
# next to a batch of fake data from G.
#
# **Loss versus training iteration**
#
# Below is a plot of D & G’s losses versus training iterations.
#
plt.figure(figsize=(10,5))
plt.title("Generator and Discriminator Loss During Training")
plt.plot(self.G_losses,label="G")
plt.plot(self.D_losses,label="D")
plt.xlabel("iterations")
plt.ylabel("Loss")
plt.legend()
#plt.show()
plt.savefig(pic_filename)
def plotSaveGprogression(self, gif_filename):
######################################################################
# **Visualization of G’s progression**
#
# Remember how we saved the generator’s output on the fixed_noise batch
# after every epoch of training. Now, we can visualize the training
# progression of G with an animation. Press the play button to start the
# animation.
#
#%%capture
fig = plt.figure(figsize=(8,8))
plt.axis("off")
ims = [[plt.imshow(np.transpose(i,(1,2,0)), animated=True)] for i in self.img_list]
ani = animation.ArtistAnimation(fig, ims, interval=1000, repeat_delay=1000, blit=True)
ani.save(gif_filename, writer='imagemagick')
#HTML(ani.to_jshtml())
def plotSaveRealFakeImage(self, pic_filename):
######################################################################
# **Real Images vs. Fake Images**
#
# Finally, lets take a look at some real images and fake images side by
# side.
#
# Grab a batch of real images from the dataloader
real_batch = next(iter(self.dataloader))
# Plot the real images
plt.figure(figsize=(15,15))
plt.subplot(1,2,1)
plt.axis("off")
plt.title("Real Images")
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(self.device)[:64], padding=5, normalize=True).cpu(),(1,2,0)))
# Plot the fake images from the last epoch
plt.subplot(1,2,2)
plt.axis("off")
plt.title("Fake Images")
plt.imshow(np.transpose(self.img_list[-1],(1,2,0)))
plt.savefig(pic_filename)
#plt.show()
######################################################################
# Where to Go Next
# ----------------
#
# We have reached the end of our journey, but there are several places you
# could go from here. You could:
#
# - Train for longer to see how good the results get
# - Modify this model to take a different dataset and possibly change the
# size of the images and the model architecture
# - Check out some other cool GAN projects
# `here <https://github.com/nashory/gans-awesome-applications>`__
# - Create GANs that generate
# `music <https://deepmind.com/blog/wavenet-generative-model-raw-audio/>`__
#
if __name__=='__main__':
setRandom()
dcgan=DCGAN()
dcgan.prepareData()
dcgan.createGen()
dcgan.createDis()
dcgan.setLossAndOptimizer()
dcgan.train()
该程序充分调用gpu进行训练

训练过程如下:

训练结果如下:









【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· AI 智能体引爆开源社区「GitHub 热点速览」
· 写一个简单的SQL生成工具