实验4
任务1
源代码
1 #include <stdio.h> 2 #define N 4 3 #define M 2 4 5 void test1() { 6 int x[N] = {1, 9, 8, 4}; 7 int i; 8 9 // 输出数组x占用的内存字节数 10 printf("sizeof(x) = %d\n", sizeof(x)); 11 12 // 输出每个元素的地址、值 13 for (i = 0; i < N; ++i) 14 printf("%p: %d\n", &x[i], x[i]); 15 16 // 输出数组名x对应的值 17 printf("x = %p\n", x); 18 } 19 20 void test2() { 21 int x[M][N] = {{1, 9, 8, 4}, {2, 0, 4, 9}}; 22 int i, j; 23 24 // 输出二维数组x占用的内存字节数 25 printf("sizeof(x) = %d\n", sizeof(x)); 26 27 // 输出每个元素的地址、值 28 for (i = 0; i < M; ++i) 29 for (j = 0; j < N; ++j) 30 printf("%p: %d\n", &x[i][j], x[i][j]); 31 printf("\n"); 32 33 // 输出二维数组名x, 以及,x[0], x[1]的值 34 printf("x = %p\n", x); 35 printf("x[0] = %p\n", x[0]); 36 printf("x[1] = %p\n", x[1]); 37 printf("\n"); 38 } 39 40 int main() { 41 printf("测试1: int型一维数组\n"); 42 test1(); 43 44 printf("\n测试2: int型二维数组\n"); 45 test2(); 46 47 return 0; 48 }
运行结果
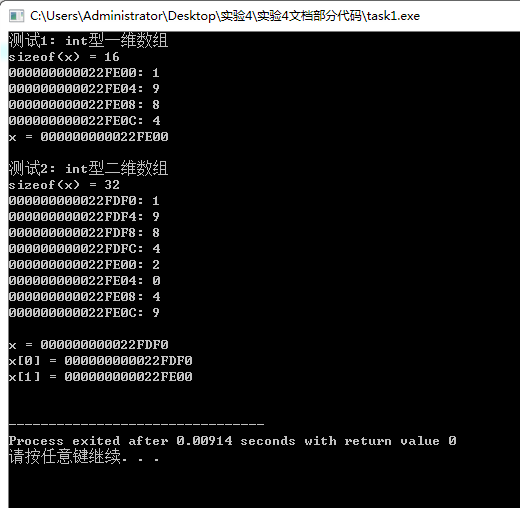
问题1:int型一维数组在内存中是连续存放的,数组名x对应的值和&x[0]是一样的
问题2:int型二维数组x在内存中是按行连续存放的,x的值和x[0],&x[0][0]一样,x[0]和x[1]相差16,是二维数组第一行占用内存地址的大小。
任务2
源代码
1 #include <stdio.h> 2 #define N 100 3 4 // 函数声明 5 void input(int x[], int n); 6 double compute(int x[], int n); 7 8 int main() { 9 int x[N]; 10 int n, i; 11 double ans; 12 13 while(printf("Enter n: "), scanf("%d", &n) != EOF) { 14 input(x, n); // 函数调用 15 ans = compute(x, n); // 函数调用 16 printf("ans = %.2f\n\n", ans); 17 } 18 19 return 0; 20 } 21 22 // 函数定义 23 void input(int x[], int n) { 24 int i; 25 26 for(i = 0; i < n; ++i) 27 scanf("%d", &x[i]); 28 } 29 30 // 函数定义 31 double compute(int x[], int n) { 32 int i, high, low; 33 double ans; 34 35 high = low = x[0]; 36 ans = 0; 37 38 for(i = 0; i < n; ++i) { 39 ans += x[i]; 40 41 if(x[i] > high) 42 high = x[i]; 43 else if(x[i] < low) 44 low = x[i]; 45 } 46 47 ans = (ans - high - low)/(n-2); 48 49 return ans; 50 }
运行结果
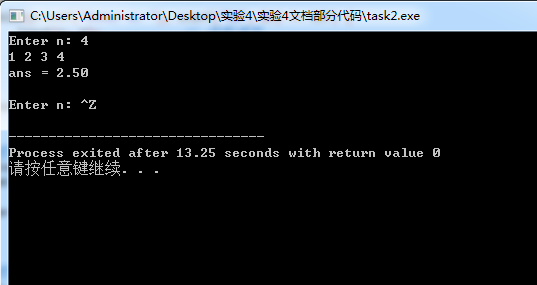
问题:函数input的功能是向数组x中输入n个数。函数compute的功能是把数组x中去掉一个最大的数和一个最小的数,再求平均值。
任务3
源代码
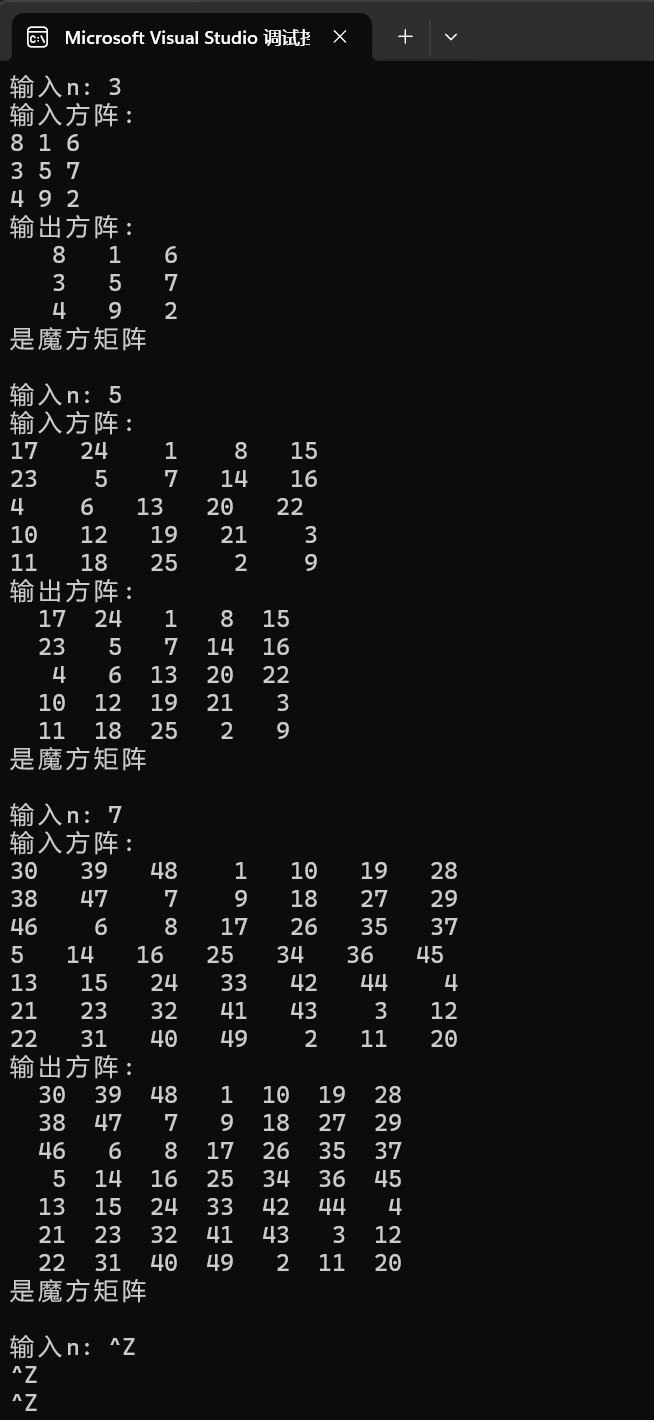
1 #include <stdio.h> 2 #define N 100 3 4 // 函数声明 5 void output(int x[][N], int n); 6 void init(int x[][N], int n, int value); 7 8 int main() { 9 int x[N][N]; 10 int n, value; 11 12 while(printf("Enter n and value: "), scanf("%d%d", &n, &value) != EOF) { 13 init(x, n, value); // 函数调用 14 output(x, n); // 函数调用 15 printf("\n"); 16 } 17 18 return 0; 19 } 20 21 // 函数定义 22 void output(int x[][N], int n) { 23 int i, j; 24 25 for(i = 0; i < n; ++i) { 26 for(j = 0; j < n; ++j) 27 printf("%d ", x[i][j]); 28 printf("\n"); 29 } 30 } 31 32 // 函数定义 33 void init(int x[][N], int n, int value) { 34 int i, j; 35 36 for(i = 0; i < n; ++i) 37 for(j = 0; j < n; ++j) 38 x[i][j] = value; 39 }
运行结果
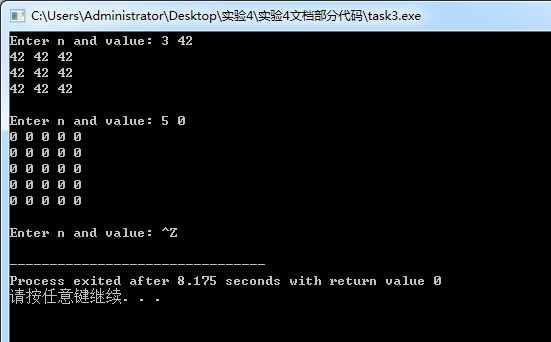
问题1:二维数组作为形参时,第二维的大小不能省略。
问题2:函数output的功能是按行逐行输出数组x中的每个元素,函数init的功能是将数组x的每个元素都赋值为value的值。
任务4
源代码
1 #include <stdio.h> 2 #define N 100 3 4 // 函数声明 5 void input(int x[],int n); 6 double median(int x[],int n); 7 8 int main() { 9 int x[N]; 10 int n; 11 double ans; 12 13 while(printf("Enter n: "), scanf("%d", &n) != EOF) { 14 input(x, n); 15 ans = median(x, n); 16 printf("ans = %g\n\n", ans); 17 } 18 19 return 0; 20 } 21 22 // 函数定义 23 void input(int x[],int n) 24 { 25 int i; 26 for (i=0;i<n;i++) 27 { 28 scanf("%d",&x[i]); 29 } 30 } 31 32 double median(int x[],int n) 33 { 34 int j,k,t; 35 for (j=0;j<n;j++) 36 { 37 for (k=0;k<n-j-1;k++) 38 { 39 if (x[k]>x[k+1]) 40 { 41 t = x [k]; 42 x[k]=x[k+1]; 43 x[k+1]=t; 44 } 45 } 46 } 47 if (n%2) 48 return x[(n-1)/2]; 49 else 50 return (x[n/2-1]+x[(n+2)/2-1])/2.0; 51 }
运行结果
任务5
源代码
1 #include <stdio.h> 2 #define N 100 3 4 // 函数声明 5 void input(int x[][N], int n); 6 void output(int x[][N], int n); 7 // 函数rotate_to_right声明 8 void rotate_to_right(int x[][N],int n); 9 10 int main() { 11 int x[N][N]; 12 int n; 13 14 printf("输入n: "); 15 scanf("%d", &n); 16 input(x, n); 17 18 printf("原始矩阵:\n"); 19 output(x, n); 20 21 // 函数rotate_to_right调用 22 rotate_to_right(x,n); 23 24 printf("变换后矩阵:\n"); 25 output(x, n); 26 27 return 0; 28 } 29 30 // 函数定义 31 // 功能: 输入一个n*n的矩阵x 32 void input(int x[][N], int n) { 33 int i, j; 34 35 for (i = 0; i < n; ++i) { 36 for (j = 0; j < n; ++j) 37 scanf("%d", &x[i][j]); 38 } 39 } 40 41 // 函数定义 42 // 功能: 输出一个n*n的矩阵x 43 void output(int x[][N], int n) { 44 int i, j; 45 46 for (i = 0; i < n; ++i) { 47 for (j = 0; j < n; ++j) 48 printf("%4d", x[i][j]); 49 50 printf("\n"); 51 } 52 } 53 54 // 函数rotate_to_right定义 55 // 功能: 把一个n*n的矩阵x,每一列向右移, 最右边被移出去的一列绕回左边 56 void rotate_to_right(int x[][N],int n) 57 { 58 int t,i,j; 59 for(i=0;i<n;i++) 60 { 61 t = x[i][n-1]; 62 for(j=n-1;j>=0;j--) 63 { 64 x[i][j]=x[i][j-1]; 65 } 66 x [i][0] = t; 67 } 68 }
运行结果
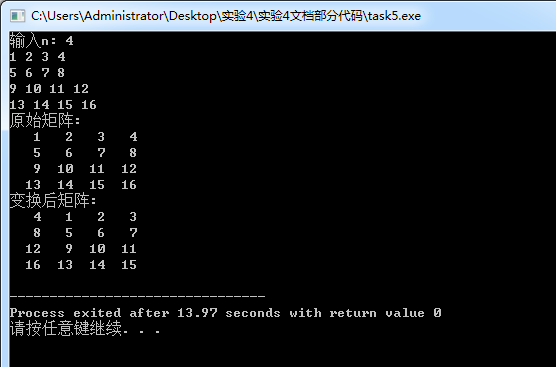
任务6
源代码
1 #include <stdio.h> 2 #define N 100 3 4 void dec_to_n(int x, int n); // 函数声明 5 6 int main() { 7 int x; 8 9 while (printf("输入十进制整数: "), scanf("%d", &x) != EOF) { 10 dec_to_n(x, 2); // 函数调用: 把x转换成二进制输出 11 dec_to_n(x, 8); // 函数调用: 把x转换成八进制输出 12 dec_to_n(x, 16); // 函数调用: 把x转换成十六进制输出 13 14 printf("\n"); 15 } 16 17 return 0; 18 } 19 20 // 函数定义 21 // 功能: 把十进制数x转换成n进制,打印输出 22 void dec_to_n(int x, int n) 23 { 24 if (n == 2) 25 { 26 27 int a[N] = { 0 }, i = 0; 28 while (x!= 0) 29 { 30 a[i] = x % 2; 31 i++; 32 x /= 2; 33 } 34 for (;i>0;i--) 35 { 36 printf("%d", a[i-1]); 37 } 38 printf("\n"); 39 } 40 if (n == 8) 41 { 42 43 int b[N] = { 0 }, k = 0; 44 while (x != 0) 45 { 46 b[k] = x % 8; 47 k++; 48 x /= 8; 49 } 50 for (; k > 0; k--) 51 { 52 printf("%d", b[k - 1]); 53 } 54 printf("\n"); 55 } 56 if (n == 16) 57 { 58 int c[N] = { 0 }, j = 0; 59 while (x != 0) 60 { 61 c[j] = x % 16; 62 j++; 63 x /= 16; 64 } 65 for (; j > 0; j--) 66 { 67 switch (c[j - 1]) 68 { 69 case 10:printf("A"); break; 70 case 11:printf("B"); break; 71 case 12:printf("C"); break; 72 case 13:printf("D"); break; 73 case 14:printf("E"); break; 74 case 15:printf("F"); break; 75 default:printf("%d", c[j - 1]); 76 } 77 } 78 printf("\n"); 79 } 80 }
运行结果
任务7
源代码
1 #include <stdio.h> 2 #define N 100 3 4 // 函数声明 5 void input(int x[][N], int n); 6 void output(int x[][N], int n); 7 // 待补足函数is_magic声明 8 int is_magic(int x[][N], int n); 9 10 int main() { 11 int x[N][N]; 12 int n; 13 14 while(printf("输入n: "), scanf("%d", &n) != EOF) { 15 printf("输入方阵:\n"); 16 input(x, n); 17 18 printf("输出方阵:\n"); 19 output(x, n); 20 21 if(is_magic(x, n)) 22 printf("是魔方矩阵\n\n"); 23 else 24 printf("不是魔方矩阵\n\n"); 25 } 26 27 return 0; 28 } 29 30 // 函数定义 31 // 功能: 输入一个n*n的矩阵x 32 void input(int x[][N], int n) { 33 int i, j; 34 35 for (i = 0; i < n; ++i) { 36 for (j = 0; j < n; ++j) 37 scanf("%d", &x[i][j]); 38 } 39 } 40 41 // 功能: 输出一个n*n的矩阵x 42 void output(int x[][N], int n) { 43 int i, j; 44 45 for (i = 0; i < n; ++i) { 46 for (j = 0; j < n; ++j) 47 printf("%4d", x[i][j]); 48 49 printf("\n"); 50 } 51 } 52 53 54 // 功能: 判断一个n阶方阵是否为魔方矩阵,如果是,返回1,否则,返回0 55 // 待补足函数is_magic定义 56 int is_magic(int x[][N],int n) 57 { 58 int i = 0, j = 0, k = 0, sum = 0, judge = 0; 59 //以第一行为标准 60 for (i = 0, j = 0; j <= n - 1;j++) 61 { 62 sum += x[i][j]; 63 } 64 //判断每行 65 for (i = 1; i <= n - 1; i++) 66 { 67 for (j = 0, judge = 0; j <= n - 1; j++) 68 { 69 judge += x[i][j]; 70 } 71 if (judge != sum) 72 { 73 return 0; 74 } 75 76 } 77 //判断每列 78 for (j = 0; j <= n - 1; j++) 79 { 80 for (i = 0, judge = 0; i <= n - 1; i++) 81 { 82 judge += x[i][j]; 83 } 84 if (judge != sum) 85 { 86 return 0; 87 } 88 } 89 //判断主对角线 90 for (i = 0, j = 0, judge = 0; i <= n - 1; i++, j++) 91 { 92 judge += x[i][j]; 93 } 94 if (judge != sum) 95 { 96 return 0; 97 } 98 //判断副对角线 99 for (i = 0, j = n - 1, judge = 0; i <= n - 1; i++, j--) 100 { 101 judge += x[i][j]; 102 } 103 if (judge != sum) 104 { 105 return 0; 106 } 107 108 return 1; 109 }
运行结果