P5212 SubString LCT+SAM

$ \color{#0066ff}{ 题目描述 }$

给定一个字符串init，要求支持两个操作

• 在当前字符串的后面插入一个字符串
• 询问字符串ss在当前字符串中出现了几次？(作为连续子串)

强制在线。

\(\color{#0066ff}{输入格式}\)

第一行一个整数\(Q\)表示操作个数

第二行一个字符串表示初始字符串init

接下来Q行，每行2个字符串Type,Str

• Type是ADD，表示在后面插入字符串。
• Type是QUERY，表示询问某字符串在当前字符串中出现了几次。

为了体现在线操作，你需要维护一个变量mask，初始值为00

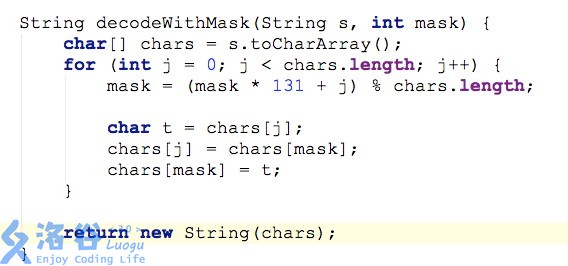
读入串Str之后，使用这个过程将之解码成真正询问的串TrueStr。

询问的时候，对TrueStr询问后输出一行答案Result

然后\(mask=mask \bigoplus Result\)

插入的时候，将TrueStr插到当前字符串后面即可。

注意：ADD和QUERY操作的字符串都需要解压

\(\color{#0066ff}{输出格式}\)

对于每一个QUERY操作，输出询问的字符串在当前字符串中出现了几次。

\(\color{#0066ff}{输入样例}\)

2
A
QUERY B
ADD BBABBBBAAB

\(\color{#0066ff}{输出样例}\)

0

\(\color{#0066ff}{数据范围与提示}\)

\(∣S∣≤6×10^5，Q \leq 10^4\),询问总长度\(\leq 3 \times 10^6\)

为防止评测过慢，对于测试点2 3 5 6 8 11 时限为3s，其余为1s

\(\color{#0066ff}{题解}\)

每次插入字符，还要匹配， 显然SAM再合适不过

匹配的时候，找到那个点\(O(len)\)，那么答案就是parent树的子树大小

但是这个树是动态的。。，于是。。。。LCT啊。。

LCT维护子树和即可

// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
const int maxn = 6e6 + 1;
const int maxm = 1.2e6 + 1;
struct LCT {
protected:
	struct node {
		node *ch[2], *fa;
		int tot, siz, val, rev;
		node(int tot = 0, int siz = 0, int val = 0, int rev = 0): tot(tot), siz(siz), val(val), rev(rev) {}
		void trn() { std::swap(ch[0], ch[1]), rev ^= 1; }
		void dwn() {
			if(!rev) return;
			if(ch[0]) ch[0]->trn();
			if(ch[1]) ch[1]->trn();
			rev = 0;
		}
		void upd() {
			tot = siz + val;
			if(ch[0]) tot += ch[0]->tot;
			if(ch[1]) tot += ch[1]->tot;
		}
		bool isr() { return fa->ch[1] == this; }
		bool ntr() { return fa && (fa->ch[1] == this || fa->ch[0] == this); }
	}pool[maxm];
	void rot(node *x) {
		node *y = x->fa, *z = y->fa;
		bool k = x->isr(); node *w = x->ch[!k];
		if(y->ntr()) z->ch[y->isr()] = x;
		(x->ch[!k] = y)->ch[k] = w;
		(y->fa = x)->fa = z;
		if(w) w->fa = y;
		y->upd(), x->upd();
	}
	void splay(node *o) {
		static node *st[maxm];
		int top;
		st[top = 1] = o;
		while(st[top]->ntr()) st[top + 1] = st[top]->fa, top++;
		while(top) st[top--]->dwn();
		while(o->ntr()) {
			if(o->fa->ntr()) rot(o->isr() ^ o->fa->isr()? o : o->fa);
			rot(o);
		}
	}
	void access(node *x) {
		for(node *y = NULL; x; x = (y = x)->fa) {
			splay(x);
			if(x->ch[1]) x->siz += x->ch[1]->tot;
			if((x->ch[1] = y)) x->siz -= x->ch[1]->tot;
			x->upd();
		}
	}
	void makeroot(node *x) { access(x), splay(x), x->trn(); }
	void link(node *x, node *y) {
		makeroot(x), access(y), splay(y);
		(x->fa = y)->siz += x->tot;
		y->upd();
	}
	void cut(node *x, node *y) {
		makeroot(y), access(x), splay(x);
		assert(x->ch[0] == y);
		x->ch[0] = y->fa = NULL, x->upd();
	}
public:
	friend struct SAM;
}c;
struct SAM {
protected: 
	struct node {
		node *ch[26], *fa;
		int len, siz;
		node(int len = 0, int siz = 0): len(len), siz(siz) {}
	}pool[maxm];
	node *root, *tail, *lst;
	LCT::node *id(node *x) { return c.pool + (x - pool); }
	void extend(int s) {
		node *o = new(tail++) node(lst->len + 1, 1), *v = lst;
		id(o)->val = 1, id(o)->upd();
		for(; v && !v->ch[s]; v = v->fa) v->ch[s] = o;
		if(!v) o->fa = root, c.link(id(o), id(root));
		else if(v->len + 1 == v->ch[s]->len) o->fa = v->ch[s], c.link(id(o), id(v->ch[s]));
		else {
			node *n = new(tail++) node(v->len + 1), *d = v->ch[s];
			std::copy(d->ch, d->ch + 26, n->ch);
			id(n)->upd();
			c.cut(id(d), id(d->fa));
			c.link(id(n), id(d->fa));
			c.link(id(d), id(n));
			c.link(id(o), id(n));
			n->fa = d->fa, d->fa = o->fa = n;
			for(; v && v->ch[s] == d; v = v->fa) v->ch[s] = n;
		}
		lst = o;
	}
	void clr() {
		tail = pool;
		root = lst = new(tail++) node();
	}
public:
	SAM() { clr(); }
	void ins(char *s) { for(char *p = s; *p; p++) extend(*p - 'A'); }
	int getans(char *s) {
		node *o = root;
		for(char *p = s; *p; p++) {
			int pos = *p - 'A';
			if(o->ch[pos]) o = o->ch[pos];
			else return 0;
		}
		c.makeroot(id(root));
		c.access(id(o));
		c.splay(id(o));
		return id(o)->val + id(o)->siz;
	}
}s;
char ls[maxn];
int n, len;
void doit(int ans) {
	for(int i = 0; i < len; i++) {
		ans = (ans * 131 + i) % len;
		std::swap(ls[i], ls[ans]);
	}
}
int main() {
	n = in();
	scanf("%s", ls);
	s.ins(ls);
	int mask = 0, ans;
	while(n --> 0) {
		scanf("%s", ls);
		if(ls[0] == 'A') {
			scanf("%s", ls);
			len = strlen(ls);
			doit(mask);
			s.ins(ls);
		}
		else {
			scanf("%s", ls);
			len = strlen(ls);
			doit(mask);
			printf("%d\n", ans = s.getans(ls));
			mask ^= ans;
		}
	}
	return 0;
}