P2173 [ZJOI2012]网络

\(\color{#0066ff}{ 题目描述 }\)

有一个无向图G，每个点有个权值，每条边有一个颜色。这个无向图满足以下两个条件：

1. 对于任意节点连出去的边中，相同颜色的边不超过两条。
2. 图中不存在同色的环，同色的环指相同颜色的边构成的环。

在这个图上，你要支持以下三种操作：

1. 修改一个节点的权值。
2. 修改一条边的颜色。
3. 查询由颜色c的边构成的图中，所有可能在节点u到节点v之间的简单路径上的节点的权值的最大值。

\(\color{#0066ff}{输入格式}\)

输入文件network.in的第一行包含四个正整数N, M, C, K，其中N为节点个数，M为边数，C为边的颜色数，K为操作数。

接下来N行，每行一个正整数vi，为节点i的权值。

之后M行，每行三个正整数u, v, w，为一条连接节点u和节点v的边，颜色为w。满足1 ≤ u, v ≤ N，0 ≤ w < C，保证u ≠ v，且任意两个节点之间最多存在一条边(无论颜色)。

最后K行，每行表示一个操作。每行的第一个整数k表示操作类型。

1. k = 0为修改节点权值操作，之后两个正整数x和y，表示将节点x的权值vx修改为y。
2. k = 1为修改边的颜色操作，之后三个正整数u, v和w，表示将连接节点u和节点v的边的颜色修改为颜色w。满足0 ≤ w < C。
3. k = 2为查询操作，之后三个正整数c, u和v，表示查询所有可能在节点u到节点v之间的由颜色c构成的简单路径上的节点的权值的最大值。如果不存在u和v之间不存在由颜色c构成的路径，那么输出“-1”。

\(\color{#0066ff}{输出格式}\)

输出文件network.out包含若干行，每行输出一个对应的信息。

1. 对于修改节点权值操作，不需要输出信息。
2. 对于修改边的颜色操作，按以下几类输出：

a) 若不存在连接节点u和节点v的边，输出“No such edge.”。

b) 若修改后不满足条件1，不修改边的颜色，并输出“Error 1.”。

c) 若修改后不满足条件2，不修改边的颜色，并输出“Error 2.”。

d) 其他情况，成功修改边的颜色，并输出“Success.”。

输出满足条件的第一条信息即可，即若同时满足b和c，则只需要输出“Error 1.”。

1. 对于查询操作，直接输出一个整数。

\(\color{#0066ff}{输入样例}\)

4 5 2 7
1
2
3
4
1 2 0
1 3 1
2 3 0
2 4 1
3 4 0
2 0 1 4
1 1 2 1
1 4 3 1
2 0 1 4
1 2 3 1
0 2 5
2 1 1 4

\(\color{#0066ff}{输出样例}\)

4
Success.
Error 2.
-1
Error 1.
5

\(\color{#0066ff}{数据范围与提示}\)

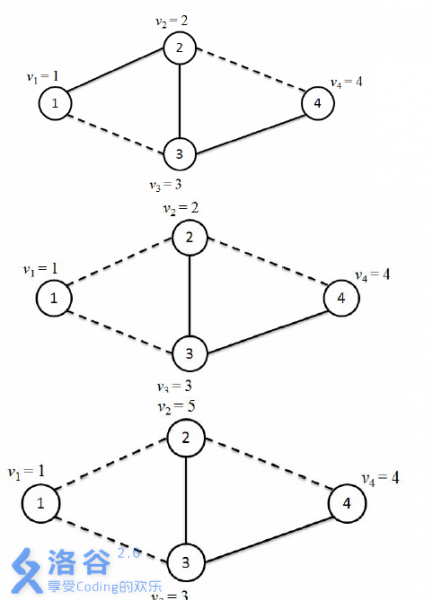
颜色0为实线的边，颜色1为虚线的边，

由颜色0构成的从节点1到节点4的路径有1 – 2 – 4，故max{v1, v2, v4} = max{ 1, 2, 4 } = 4。

将连接节点1和节点2的边修改为颜色1，修改成功，输出“Success.”

将连接节点4和节点3的边修改为颜色1，由于修改后会使得存在由颜色1构成的环( 1 – 2 – 4 – 3 – 1 )，不满足条件2，故不修改，并输出“Error 2”。

不存在颜色0构成的从节点1到节点4的边，输出“-1”。

将连接节点2和节点3的边修改为颜色1，由于修改后节点2的连出去的颜色为1的边有3条，故不满足条件1，故不修改，并输出“Error 1.”。

将节点2的权值修改为5。

由颜色1构成的从节点1到节点4的路径有 1 – 2 – 4，故max{v1, v2, v4} = max{ 1, 5, 4 } = 5。

【数据规模】

对于30%的数据：N ≤ 1000，M ≤ 10000，C ≤ 10，K ≤ 1000。

另有20%的数据：N ≤ 10000，M ≤ 100000，C = 1，K ≤ 100000。

对于100%的数据：N ≤ 10000，M ≤ 100000，C ≤ 10，K ≤ 100000。

\(\color{#0066ff}{ 题解 }\)

不存在同色环，那么每种颜色就是个森林

颜色只有10个，点数才10000，乘起来不过才1e5，所以用LCT维护再合适不过

LCT支持单点修改，树链查询，对于颜色修改，只需在原颜色的LCT上cut一下，新颜色link一下就行

这题的判断比较麻烦

首先对于改颜色，我们需要找到那个边，可以map套一个pair记录这条边当前的颜色以及是否存在的问题

对于a，直接map查找即可

对于b，我们开个桶记录一下，每个点的出边的颜色

注意，修改前后的颜色可能是一样的，要判掉

对于c，同颜色成环的问题，也就是修改后的颜色的LCT上x与y以及联通

但是还要特判修改前后的颜色是否相同，如果相同，那cut之后再link依然不会成环

查询直接在对应颜色琛出一条链输出即可

#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
using std::map;
using std::pair;
using std::make_pair;
const int maxn = 1e4 + 10;
struct LCT {
protected:
	struct node {
		node *ch[2], *fa;
		int val, max, rev;
		node(int val = 0, int max = 0, int rev = 0): val(val), max(max), rev(rev) { ch[0] = ch[1] = fa = NULL; }
		void trn() { std::swap(ch[0], ch[1]), rev ^= 1; }
		void upd() {
			max = val;
			if(ch[0]) max = std::max(max, ch[0]->max);
			if(ch[1]) max = std::max(max, ch[1]->max); 
		}
		void dwn() {
			if(!rev) return;
			if(ch[0]) ch[0]->trn();
			if(ch[1]) ch[1]->trn();
			rev = 0;
		}
		bool ntr() { return fa && (fa->ch[0] == this || fa->ch[1] == this); }
		bool isr() { return this == fa->ch[1]; }
	}pool[maxn];
	void rot(node *x) {
		node *y = x->fa, *z = y->fa;
		bool k = x->isr(); node *w = x->ch[!k];
		if(y->ntr()) z->ch[y->isr()] = x;
		x->ch[!k] = y, y->ch[k] = w;
		y->fa = x, x->fa = z;
		if(w) w->fa = y;
		y->upd(), x->upd();
	}
	void splay(node *o) {
		static node *st[maxn];
		int top;
		st[top = 1] = o;
		while(st[top]->ntr()) st[top + 1] = st[top]->fa, top++;
		while(top) st[top--]->dwn();
		while(o->ntr()) {
			if(o->fa->ntr()) rot(o->isr() ^ o->fa->isr()? o : o->fa);
			rot(o);
		}
	}
	void access(node *x) {
		for(node *y = NULL; x; x = (y = x)->fa) 
			splay(x), x->ch[1] = y, x->upd();
	}
	void makeroot(node *x) { access(x), splay(x), x->trn(); }
	node *findroot(node *x) {
		access(x), splay(x);
		while(x->dwn(), x->ch[0]) x = x->ch[0];
		return x;
	}
public:
	void init(int id, int val) { pool[id].val = val, pool[id].upd(); }
	void link(int l, int r) {
		node *x = pool + l, *y = pool + r;
		makeroot(x), x->fa = y;
	}
	void cut(int l, int r) {
		node *x = pool + l, *y = pool + r;
		makeroot(x), access(y), splay(y);
		if(y->ch[0] == x) y->ch[0] = x->fa = NULL;
	}
	void change(int pos, int k) {
		node *o = pool + pos;
		splay(o);
		o->val = k, o->upd();
	}
	bool judge(int x, int y) { return findroot(pool + x) == findroot(pool + y); }
	int query(int l, int r) {
		if(!judge(l, r)) return -1;
		node *x = pool + l, *y = pool + r;
		makeroot(x), access(y), splay(y);
		return y->max;
	}
}s[10];
int n, m, c, k;
map<pair<int, int>, int> mp;
int num[maxn][12];
int main() {
	n = in(), m = in(), c = in(), k = in();
	for(int i = 1; i <= n; i++) {
		int val = in();
		for(int j = 0; j < c; j++) 
			s[j].init(i, val);
	}
	int p, x, y, v;
	for(int i = 1; i <= m; i++) {
		x = in(), y = in(), v = in();
		if(x > y) std::swap(x, y);
		mp[make_pair(x, y)] = v + 1;
		s[v].link(x, y);
		num[x][v]++, num[y][v]++;
	}
	while(k --> 0) {
		p = in();
		if(p == 0) {
			x = in(), y = in();
			for(int i = 0; i < c; i++) s[i].change(x, y);
		}
		if(p == 1) {
			x = in(), y = in(), v = in();
			if(x > y) std::swap(x, y);
			if(!mp.count(make_pair(x, y))) {
				printf("No such edge.\n");
				continue;
			}
			if(mp[make_pair(x, y)] - 1 != v && (num[x][v] > 1 || num[y][v] > 1)) {
				printf("Error 1.\n");
				continue;
			}
			if(mp[make_pair(x, y)] - 1 != v && s[v].judge(x, y)) {
				printf("Error 2.\n");
				continue;
			}
			num[x][mp[make_pair(x, y)] - 1]--, num[y][mp[make_pair(x, y)] - 1]--;
			num[x][v]++, num[y][v]++;
			s[mp[make_pair(x, y)] - 1].cut(x, y);
			mp[make_pair(x, y)] = v + 1;
			s[v].link(x, y);
			printf("Success.\n");
		}
		if(p == 2) v = in(), x = in(), y = in(), printf("%d\n", s[v].query(x, y));
	}
	return 0;
}