P2387 [NOI2014]魔法森林 LCT维护最小生成树

\(\color{#0066ff}{ 题目描述 }\)

为了得到书法大家的真传，小 E 同学下定决心去拜访住在魔法森林中的隐 士。魔法森林可以被看成一个包含 n 个节点 m 条边的无向图，节点标号为 1,2,3,…,n，边标号为 1,2,3,…,m。初始时小 E 同学在 1 号节点，隐士则住在 n 号节点。小 E 需要通过这一片魔法森林，才能够拜访到隐士。

魔法森林中居住了一些妖怪。每当有人经过一条边的时候，这条边上的妖怪 就会对其发起攻击。幸运的是，在 1 号节点住着两种守护精灵：A 型守护精灵与 B 型守护精灵。小 E 可以借助它们的力量，达到自己的目的。

只要小 E 带上足够多的守护精灵，妖怪们就不会发起攻击了。具体来说，无 向图中的每一条边 ei 包含两个权值 ai 与 bi 。若身上携带的 A 型守护精灵个数不 少于 ai ，且 B 型守护精灵个数不少于 bi ，这条边上的妖怪就不会对通过这条边 的人发起攻击。当且仅当通过这片魔法森林的过程中没有任意一条边的妖怪向 小 E 发起攻击，他才能成功找到隐士。

由于携带守护精灵是一件非常麻烦的事，小 E 想要知道，要能够成功拜访到 隐士，最少需要携带守护精灵的总个数。守护精灵的总个数为 A 型守护精灵的 个数与 B 型守护精灵的个数之和。

\(\color{#0066ff}{输入格式}\)、

输入文件的第 1 行包含两个整数 n,m，表示无向图共有 n 个节点，m 条边。 接下来 m 行，第i+ 1 行包含 4 个正整数 Xi,Yi,ai,bi，描述第i条无向边。 其中Xi与 Yi为该边两个端点的标号，ai 与 bi 的含义如题所述。 注意数据中可能包含重边与自环。

\(\color{#0066ff}{输出格式}\)

输出一行一个整数：如果小 E 可以成功拜访到隐士，输出小 E 最少需要携 带的守护精灵的总个数；如果无论如何小 E 都无法拜访到隐士，输出“-1”（不 含引号）。

\(\color{#0066ff}{输入样例}\)

4 5 
1 2 19 1 
2 3 8 12 
2 4 12 15 
1 3 17 8 
3 4 1 17 
    
    
    
3 1 
1 2 1 1 

\(\color{#0066ff}{输出样例}\)

32

    
-1

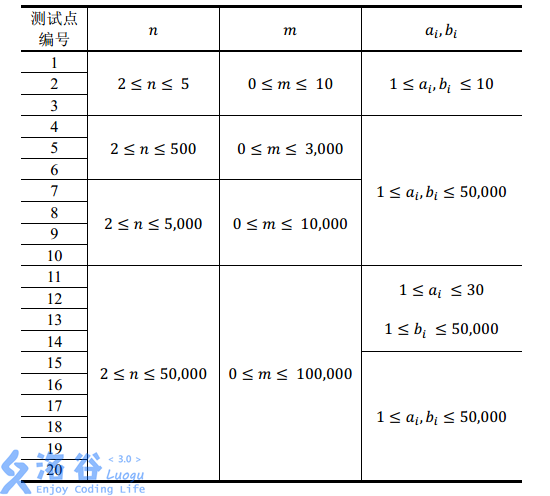
\(\color{#0066ff}{数据范围与提示}\)

* 解释1

如果小 E 走路径 1→2→4，需要携带 19+15=34 个守护精灵； 如果小 E 走路径 1→3→4，需要携带 17+17=34 个守护精灵； 如果小 E 走路径 1→2→3→4，需要携带 19+17=36 个守护精灵； 如果小 E 走路径 1→3→2→4，需要携带 17+15=32 个守护精灵。 综上所述，小 E 最少需要携带 32 个守护精灵。

* 解释2

小 E 无法从 1 号节点到达 3 号节点，故输出-1。

\(\color{#0066ff}{ 题解 }\)

把所有边按a排序，用LCT维护边权为b的生成树（注意新加点使边权变成点权）

每次向内加边，a已知（已排序），把链上最大的b换下来，每次取min即可

#include<bits/stdc++.h>
#define LL long long
LL in() {
    char ch; LL x = 0, f = 1;
    while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
    for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
    return x * f;
}
const int maxn = 5e4 + 100;
const int inf = 0x7fffffff;
struct node {
    int x, y, a, b;
    friend bool operator < (const node &a, const node &b) { return a.a < b.a; }
}e[maxn << 1];
struct LCT {
protected:
    struct node {
        node *fa, *ch[2];
        int max, val, rev;
        node(int max = 0, int val = 0, int rev = 0): max(max), val(val), rev(rev) {}
        void trn() { std::swap(ch[0], ch[1]); rev ^= 1; }
        void upd() {
            max = val;
            if(ch[0]) max = std::max(max, ch[0]->max);
            if(ch[1]) max = std::max(max, ch[1]->max);
        }
        void dwn() {
            if(!rev) return;
            if(ch[0]) ch[0]->trn();
            if(ch[1]) ch[1]->trn();
            rev = 0;
        }
        bool ntr() { return fa && (fa->ch[1] == this || fa->ch[0] == this); }
        bool isr() { return this == fa->ch[1]; }
        void clr() {
            if(ch[0]) ch[0]->fa = NULL;
            if(ch[1]) ch[1]->fa = NULL;
            ch[0] = ch[1] = NULL;
        }
    }pool[maxn << 2];
    void rot(node *x) {
        node *y = x->fa, *z = y->fa;
        bool k = x->isr(); node *w = x->ch[!k];
        if(y->ntr()) z->ch[y->isr()] = x;
        x->ch[!k] = y, y->ch[k] = w;
        y->fa = x, x->fa = z;
        if(w) w->fa = y;
        y->upd(), x->upd();
    }
    void splay(node *o) {
        static node *st[maxn << 2];
        int top;
        st[top = 1] = o;
        while(st[top]->ntr()) st[top + 1] = st[top]->fa, top++;
        while(top) st[top--]->dwn();
        while(o->ntr()) {
            if(o->fa->ntr()) rot(o->isr() ^ o->fa->isr()? o : o->fa);
            rot(o);
        }
    }
    void access(node *x) {
        for(node *y = NULL; x; x = (y = x)->fa)
            splay(x), x->ch[1] = y, x->upd();
    }
    void makeroot(node *x) { access(x), splay(x), x->trn(); }
    node *findroot(node *x) {
        access(x), splay(x);
        while(x->dwn(), x->ch[0]) x = x->ch[0];
        return x;
    }
    void link(node *x, node *y) { makeroot(x), x->fa = y; }
    node *findpos(node *x, int max) {
        while(x->dwn(), x->val != max) {
            if(x->ch[0] && x->ch[0]->max == max) x = x->ch[0];
            else x = x->ch[1];
        }
        return x;
    }
public:
    void init(::node *a,int n, int m) { 
        for(int i = n + 1; i <= n + m; i++) 
            pool[i].val = a[i - n].b, pool[i].upd();
    }
    void add(const ::node &a, int id) {
        node *x = pool + a.x, *y = pool + a.y;
        node *o = pool + id;
        if(findroot(x) == findroot(y)) {
            makeroot(x), access(y), splay(y);
            if(a.b >= y->max) return;
            node *d = findpos(y, y->max);
            splay(d);
            d->clr(), d->upd();
        }
        link(x, o), link(o, y);
    }
    int query(int l, int r) {
        node *x = pool + l, *y = pool + r;
        if(findroot(x) != findroot(y)) return -1;
        makeroot(x), access(y), splay(y);
        return y->max;
    }
}s;
int n, m, ans = inf;
int main() {
    n = in(), m = in();
    for(int i = 1; i <= m; i++) 
        e[i].x = in(), e[i].y = in(), e[i].a = in(), e[i].b = in();
    std::sort(e + 1, e + m + 1);
    s.init(e, n, m);
    for(int i = 1; i <= m; i++) {
        s.add(e[i], i + n);
        int v = s.query(1, n);
        if(v == -1) continue;
        ans = std::min(ans, v + e[i].a);
    }
    printf("%d", ans == inf? -1 : ans);
    return 0;
}