BZOJ 2725 [Violet 6]故乡的梦 线段树+最短路树

\(\color{#0066ff}{ 题目描述 }\)

\(\color{#0066ff}{输入格式}\)

\(\color{#0066ff}{输出格式}\)

\(\color{#0066ff}{输入样例}\)

6 7 
1 2 1 
2 3 1 
3 4 2 
4 5 1 
5 6 1 
1 3 3
4 6 3 
1 6 
4 
1 2
1 3 
4 3 
6 5 

\(\color{#0066ff}{输出样例}\)

7
6
Infinity
7

\(\color{#0066ff}{数据范围与提示}\)

\(\color{#0066ff}{ 题解 }\)

分别从s和t跑最短路，构建出最短路树

标记最短路树的点和边

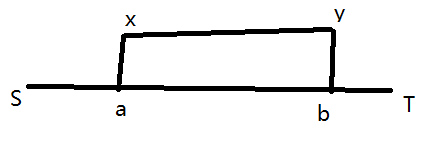
从最短路树上的每个点bfs，找到能影响的L和R

显然若上图a，b之间的某条边断了，x到y的边就可以用来更新这部分答案

从a找到所有x，b找到所有y

枚举所有边，只要不在最短路树上，就类似于上图更新（用线段树维护）

在\(O(nlogn)\)的复杂度下求出删去每条最短路树上的边的ans

对于询问，如果不是最短路树的边，ans就是最短路

否则用刚刚在线段树求的ans输出

跑dij的pair要开long long！！！！

#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
const int maxn = 2e6 + 100;
int L[maxn], R[maxn], S, T;
int n, m;
struct node {
	int to;
	LL dis;
	bool vis;
	node *nxt;
	node(int to = 0, LL dis = 0, bool vis = false, node *nxt = NULL): to(to), dis(dis), vis(vis), nxt(nxt) {}
};
node *head[maxn];
bool vis[maxn];
LL diss[maxn], dist[maxn];
int st[maxn], cnt, rst[maxn];
LL ans[maxn];
const LL inf = 9999999999999LL;
using std::pair;
using std::make_pair;
struct Tree {
	Tree *ch[2];
	LL val;
	int l, r;
	Tree(LL val = 0, int l = 0, int r = 0): val(val), l(l), r(r) {}
}*root;
void build(Tree *&o, int l, int r) {
	o = new Tree(inf, l, r);
	if(l == r) return;
	int mid = (l + r) >> 1;
	build(o->ch[0], l, mid);
	build(o->ch[1], mid + 1, r);
}
void add(int from, int to, LL dis) {
	head[from] = new node(to, dis, 0, head[from]);
}
void dij(int s, LL *dis) {
	std::priority_queue<pair<LL, int>, std::vector<pair<LL, int> >, std::greater<pair<LL, int> > > q;
	for(int i = 1; i <= n; i++) vis[i] = 0, dis[i] = inf;
	q.push(make_pair(dis[s] = 0, s));
	while(!q.empty()) {
		int tp = q.top().second;
		q.pop();
		if(vis[tp]) continue;
		vis[tp] = true;
		for(node *i = head[tp]; i; i = i->nxt)
			if(dis[i->to] > dis[tp] + i->dis)
				q.push(make_pair(dis[i->to] = dis[tp] + i->dis, i->to));
	}
}
void bfs(int s, int *P, LL *dis) {
	std::queue<int> v;
	P[st[s]] = s;
	v.push(st[s]);
	while(!v.empty()) {
		int tp = v.front(); v.pop();
		for(node *i = head[tp]; i; i = i->nxt) {
			if(dis[i->to] == dis[tp] + i->dis && !vis[i->to] && !P[i->to]) {
				P[i->to] = s;
				v.push(i->to);
			}
		}
	}
}
void change(Tree *o, int l, int r, LL val) {
	if(o->r < l || o->l > r) return;
	if(l <= o->l && o->r <= r) return (void)(o->val = std::min(o->val, val));
	change(o->ch[0], l, r, val), change(o->ch[1], l, r, val);
}
void query(Tree *o) {
	if(o->l == o->r) return (void)(ans[o->l] = o->val);
	o->ch[0]->val = std::min(o->ch[0]->val, o->val);
	o->ch[1]->val = std::min(o->ch[1]->val, o->val);
	query(o->ch[0]);
	query(o->ch[1]);
}
int main() {
	n = in(), m = in();
	LL x, y, z;
	for(int i = 1; i <= m; i++) {
		x = in(), y = in(), z = in();
		add(x, y, z), add(y, x, z);
	}
	dij(S = in(), diss);
	dij(T = in(), dist);
	for(int i = 1; i <= n; i++) vis[i] = 0;
	for(int o = S; o != T;) {
		st[rst[o] = ++cnt] = o;
		vis[o] = true;
		for(node *i = head[o]; i; i = i->nxt) {
			if(diss[o] + dist[i->to] + i->dis == diss[T]) {
				i->vis = true;
				o = i->to;
				break;
			}
		}
	}
	st[rst[T] = ++cnt] = T;
	vis[T] = true;
	for(int i = 1; i <= cnt; i++) bfs(i, L, diss);
	for(int i = cnt; i >= 1; i--) bfs(i, R, dist);
	build(root, 1, cnt);
	for(int i = 1; i <= n; i++) 
		for(node *j = head[i]; j; j = j->nxt) {
			if(j->vis) continue;
			if(L[i] < R[j->to] && L[i] && R[j->to]) change(root, L[i], R[j->to] - 1, diss[i] + dist[j->to] + j->dis);
		}
	query(root);
	for(int q = in(); q --> 0;) {
		x = in(), y = in();
		if(rst[x] > 0 && rst[y] > 0 && abs(rst[x] - rst[y]) == 1) {
			LL t = ans[std::min(rst[x], rst[y])];
			if(t == inf) printf("Infinity\n");
			else printf("%lld\n", t);
		}
		else if(diss[T] == inf) printf("Infinty\n");
		else printf("%lld\n", diss[T]);
	}
	return 0;
}