平衡树学习笔记(3)-------Splay
Splay
Splay是一个实用而且灵活性很强的平衡树
效率上也比较客观,但是一定要一次性写对
debug可能不是那么容易
Splay作为平衡树,它的平衡方式就是旋转
暴力旋转,赤裸裸的旋转,各种旋转
就是依靠玄学的旋转来保证自己的复杂度
不废话,上主题
\(\color{#9900ff}{定义}\)
struct node {
node *ch[2], *fa; //父亲,孩子
int val, siz; //权值,大小
node(node *fa = NULL, int val = 0, int siz = 0): fa(fa), val(val), siz(siz) { ch[0] = ch[1] = NULL; } //不写构造函数一时爽,一直不写一直爽~~~
bool isr() { return this == fa->ch[1]; } //当前点是否为父亲右孩子,旋转的时候用,方便
int rk() { return ch[0]? ch[0]->siz + 1 : 1; } //当前的排名
void upd() { siz = 1 + (ch[0]? ch[0]->siz : 0) + (ch[1]? ch[1]->siz : 0); } //维护信息
}pool[maxn], *tail, *root, *st[maxn]; //内存池与回收池,还有根节点
\(\color{#9900ff}{基本操作}\)
1、rotate
其实这个就是第一节说的旋转
rot(x)代表把x转到它父亲的位置上去
这也是Splay维护平衡的基础
下面是重点了!!

把x转到它父亲y上
以下代码中字母对应,其中那个R是代码中的w(因为为中间量,要特殊对待)
void rot(node *x) {
node *y = x->fa, *z = y->fa;
//找到y,z(注意,x转上去后,z的孩子变成x,所以要涉及到z)
bool k = x->isr(); node *w = x->ch[!k];
//isr是bool型的,看看是不是自己父亲的右孩子,这个旋转针对的是所有情况,不仅仅是上图的情况
if(y != root) z->ch[y->isr()] = x;
else root = x;
//x转上去,就要考虑y是不是根的问题
//如果y是根,x转上去后,自然成为了根
//如果不是根,就要让x替换y的位置,原来y是z的哪个孩子,现在x就是z的哪个孩子
x->ch[!k] = y, y->ch[k] = w;
//该认孩子的认孩子
y->fa = x, x->fa = z;
//该认父亲的认父亲
if(w) w->fa = y;
//判空
y->upd(), x->upd();
//因为x在y的上一层,x的upd要基于y,所以y先来
}
以上部分一定要理解透彻!!!
2、Splay
这个操作使基于rotate的
Splay(x),作用是把x转到根节点的位置上
显然要转好多次的qwq
因为一些玄学的东西(雾
平衡树中,每次用到谁转谁(反正不影响性质,说白了貌似还是瞎转)
这样玄学的操作可以使Splay平衡
void splay(node *x) {
while(x != root) {
if(x->fa != root) rot(x->isr() ^ x->fa->isr()? x : x->fa);
rot(x);
}
}
上面if那一行是啥意思呢?
我们要考虑一条链的情况
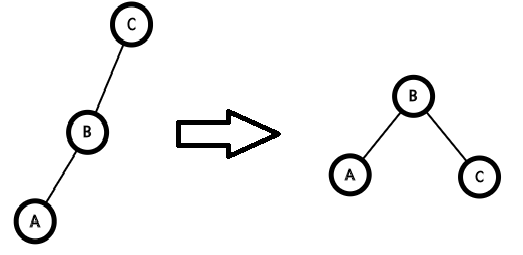
这种情况我们要先转父亲,再转自己
否则直接转自己就行
至此,基本操作已经结束qwq
\(\color{#9900ff}{其它操作}\)
1、插入
这个是真的暴力插。。。。。。
void ins(int val) {
if(!root) return (void)(root = new(top? st[top--] : tail++) node(NULL, val, 1));
//空树则对根节点操作
node *o = root, *fa = NULL;
//从根开始暴力插♂
while(o) {
fa = o;
//记录父亲
//一直往下跳(注意方向)
if(val <= o->val) o = o->ch[0];
else o = o->ch[1];
}
//跳到了空节点上,那么申请新节点
o = new(top? st[top--] : tail++) node(fa, val, 1);
fa->ch[val > fa->val] = o;
//玄学操作,转上去
splay(o);
}
2、删除
这个有点。。鬼畜
一般来说,(我所知道的)有两种删除方式,某崔性男子说可以merge(雾
第一种
找到要删节点的前驱和后继
前驱转到根,后继转到根的右孩子
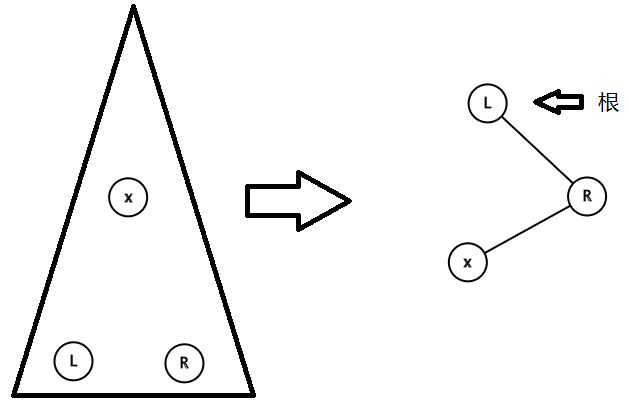
R的左子树一定是我们要删的,直接删就行了(父子不互认,其他变量清空)
第二种
需要两个函数(好像有点麻烦吧qwq)
node *lst() {
node *o = root->ch[0];
while(o->ch[1] != null) o = o->ch[1];
return o;
}
返回根的前驱
下面的是真正的删除
首先把要删的节点转到根并记录一下
找到根的前驱
把根的前驱转到根
那么一定是这种情况
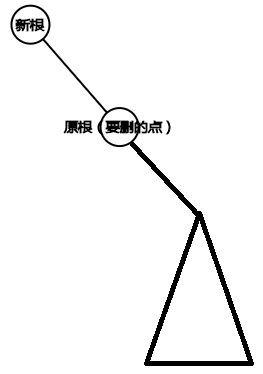
原根,也就是要删的点,一定是没有左孩子的!!!!
所以类似于链表的操作,把该删的删掉
inline void del(int x) {
rnk(x);
nod l=lst(),rt=root;
splay(l);
//类似于链表的操作,使得被删点隔绝于此树之外
l->ch[1] = rt->ch[1];
l->ch[1]->fa = l;
rt->clr();
l->upd();
//清空与维护
}
3、查询数x的排名
暴力找
int rnk(int val) {
//rank来记录排名
//从根开始暴力求
node *o = root, *lst = NULL; int rank = 0;
while(o) {
lst = o;
if(val <= o->val) o = o->ch[0];
else rank += o->rk(), o = o->ch[1];
}
return splay(lst), rank + 1;
}
4、查询第k大的数
其实跟上面差不多
int kth(int k) {
node *o = root;
while(o && o->rk() != k) {
if(o->rk() > k) o = o->ch[0];
else k -= o->rk(), o = o->ch[1]; // 别忘减去左子树的贡献
}
return splay(o), o->val;
}
5、6、前驱,后继
这两个为什么一块写?
因为他们几乎一样
int pre(int val) {
node *o = root, *lst = root;
while(o) {
if(o->val < val) lst = o, o = o->ch[1]; //成立的时候要记录一下,下面同理
else o = o->ch[0];
}
return lst->val;
}
int nxt(int val) {
node *o = root, *lst = root;
while(o) {
if(o->val > val) lst = o, o = o->ch[0];
else o = o->ch[1];
}
return lst->val;
}
至此,Splay完
其实只要理解了,并不是想象那么难的
放一下完整代码
#include<bits/stdc++.h>
#define LL long long
LL in() {
char ch; LL x = 0, f = 1;
while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
return x * f;
}
const int maxn = 1e5 + 100;
struct Splay {
protected:
struct node {
node *ch[2], *fa;
int val, siz;
node(node *fa = NULL, int val = 0, int siz = 0): fa(fa), val(val), siz(siz) { ch[0] = ch[1] = NULL; }
bool isr() { return this == fa->ch[1]; }
int rk() { return ch[0]? ch[0]->siz + 1 : 1; }
void upd() { siz = 1 + (ch[0]? ch[0]->siz : 0) + (ch[1]? ch[1]->siz : 0); }
}pool[maxn], *tail, *root, *st[maxn];
int top;
void rot(node *x) {
node *y = x->fa, *z = y->fa;
bool k = x->isr(); node *w = x->ch[!k];
if(y != root) z->ch[y->isr()] = x;
else root = x;
x->ch[!k] = y, y->ch[k] = w;
y->fa = x, x->fa = z;
if(w) w->fa = y;
y->upd(), x->upd();
}
void splay(node *o) {
while(o != root) {
if(o->fa != root) rot(o->isr() ^ o->fa->isr()? o : o->fa);
rot(o);
}
}
node *merge(node *x, node *y, node *fa) {
if(x) x->fa = fa;
if(y) y->fa = fa;
if(!x || !y) return x? x : y;
if(rand() & 1) return x->ch[1] = merge(x->ch[1], y, x), x->upd(), x;
else return y->ch[0] = merge(x, y->ch[0], y), y->upd(), y;
}
public:
Splay() { tail = pool, top = 0; }
int rnk(int val) {
node *o = root, *lst = NULL; int rank = 0;
while(o) {
lst = o;
if(val <= o->val) o = o->ch[0];
else rank += o->rk(), o = o->ch[1];
}
return splay(lst), rank + 1;
}
int kth(int k) {
node *o = root;
while(o && o->rk() != k) {
if(o->rk() > k) o = o->ch[0];
else k -= o->rk(), o = o->ch[1];
}
return splay(o), o->val;
}
void ins(int val) {
if(!root) return (void)(root = new(top? st[top--] : tail++) node(NULL, val, 1));
node *o = root, *fa = NULL;
while(o) {
fa = o;
if(val <= o->val) o = o->ch[0];
else o = o->ch[1];
}
o = new(top? st[top--] : tail++) node(fa, val, 1);
fa->ch[val > fa->val] = o;
splay(o);
}
void del(int val) {
node *o = root;
while(o && o->val != val) {
if(val < o->val) o = o->ch[0];
else o = o->ch[1];
}
if(!o) return;
splay(o);
root = merge(o->ch[0], o->ch[1], NULL);
st[++top] = o;
}
int pre(int val) {
node *o = root, *lst = root;
while(o) {
if(o->val < val) lst = o, o = o->ch[1];
else o = o->ch[0];
}
return lst->val;
}
int nxt(int val) {
node *o = root, *lst = root;
while(o) {
if(o->val > val) lst = o, o = o->ch[0];
else o = o->ch[1];
}
return lst->val;
}
}v;
int main() {
int p, x;
for(int T = in(); T --> 0;) {
p = in(), x = in();
if(p == 1) v.ins(x);
if(p == 2) v.del(x);
if(p == 3) printf("%d\n", v.rnk(x));
if(p == 4) printf("%d\n", v.kth(x));
if(p == 5) printf("%d\n", v.pre(x));
if(p == 6) printf("%d\n", v.nxt(x));
}
return 0;
}
----olinr


 浙公网安备 33010602011771号
浙公网安备 33010602011771号