平衡树学习笔记（1）-------简介

平衡树是一个很神奇的数据结构

noip前，学了其两种实现方式，Splay和Treap，非常实用（虽然码量有点。。）

每个平衡树都是二叉查找树，保证\(左孩子 \leq 自己 \leq 右孩子\)

因此，平衡树的中序遍历就是插入节点的有序序列（理解一下）

平衡树支持插入，删除，以及各种查询，以下面为例

\(\color{#0066ff}{题目描述}\)

您需要写一种数据结构，来维护一些数，其中需要提供以下操作：

插入数x

删除x数x(若有多个相同的数，只删除一个)
查询数x的排名(排名定义为比当前数小的数的个数+1。若有多个相同的数，输出最小的排名)

查询排名为x的数

求x的前驱(前驱定义为小于x，且最大的数)

求x的后继(后继定义为大于x，且最小的数)

\(\color{#0066ff}{输入格式}\)

第一行为n，表示操作的个数,下面nn行每行有两个数opt和x，opt表示操作的序号\(1\leq opt \leq 6\)

\(\color{#0066ff}{输出格式}\)

对于操作3,4,5,6每行输出一个数，表示对应答案

\(\color{#0066ff}{输入样例}\)

10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598

\(\color{#0066ff}{输出样例}\)

106465
84185
492737

这就是洛谷P3369普通平衡树板子

总的来说，平衡树的实现方式有6种：SBT，Splay，Treap，AVL，RBT，替罪羊

其实还有一个是普通的二叉查找树：BST，由于太过辣鸡。。。很容易被卡，此处不提

对于AVL，实用性比较低，比如代码长度，精简度不如SBT，速度倒是差不多，对大数据的处理不如RBT，对可持久化的支持又不如FAQ，灵活性又没有Splay高，还不能像替罪羊树那样支持树套树，此处也不提了

那么，这些平衡树根BST有啥区别呢，为什么平衡树要比BST快好多好多呢？

试想一下，当插入的节点使树变成一条链时，每次查找最坏岂不是\(O(n)\)？ 显然TLE。。。

这些平衡树，各有各的长处，每一个都有骚操作使自己平衡，防止复杂度过高

大部分平衡树要依靠旋转（除了Treap，替罪羊）

这里，把旋转提一下

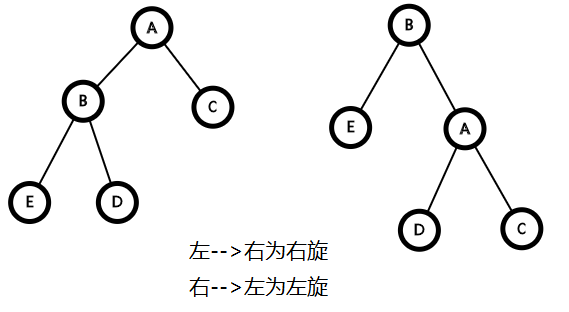
刚刚说，平衡树的\(左孩子 \leq 自己 \leq 右孩子\)

因此上图中\(E < B < D < A < C\)

两个根A，B互转，D作为[A,B]内的一个元素，必须要保证它的位置（如图）

这就是一般平衡树的旋转操作

接下来，会依次介绍Treap，Splay，替罪羊树，SBT，RBT

下一篇：平衡树学习笔记（2）-------Treap